基于Sagaseta 理论的桩基挤土效应计算
2013-08-21孟庆明
董 博 孟庆明
(中国水电建设集团铁路建设有限公司,北京 100048)
1 概述
在桩基施工时,特别是在密集建筑群中桩基施工时,无论是动力打桩还是静力压桩,由于桩的挤土效应所造成对周围土体的影响问题,一直为岩土工程学者所关注。
桩入土必定排开一定体积的土体,改变桩周土体应力状态,扰动附近土层,产生深层土体塑性流动,地表一定范围内出现隆起、沉降和水平位移。此外,桩的沉入过程对周围土体来说是一个不排水过程,会产生高孔隙水压力,当过程结束后,孔隙水压力消散,桩周土体发生固结,导致土体有效应力增加、桩周土体下沉、桩的承载力降低。
此前的沉桩影响研究,多数是揭示了发生挤土后,桩周土体的应力分布和土体变形的规律,关于挤土范围的影响并不理想,特别是单纯用小孔扩张理论估计的结果同样不理想。对此问题目前尚缺乏完整的、系统的和成熟的理论和计算方法,大多数是依靠工程技术人员的经验和直观判断来解决,工程事故时有发生,给国家和人民的生命财产造成巨大的损失。
2 公式推导
在开始分析时不考虑土体表面影响而把土体看作无限介质。由于沉桩过程中桩周土体的变化复杂、分析会遇到土力学及数学上的困难,在不影响工程精度的前提下做如下假定:
1)桩周土体为均匀、各向同性、半无限弹性体。
2)打桩是一个准静态过程,不考虑打桩的动力效应。
3)打桩期间土体处于不排水状态,不考虑土体的压缩,仅考虑其整体向周围的运动。
4)打桩为一轴对称问题。
在开始分析时,不考虑土体表面的影响,由于假设沉降是在无限介质中计算土的应变。而实际土体是半无限介质,由此假设而得到的应变将在土体的自由表面产生应力,这与土体表面实际无应力状态是不相符的。因此采用存在一个假设的虚拟负对称点的方法来消除这些应力。
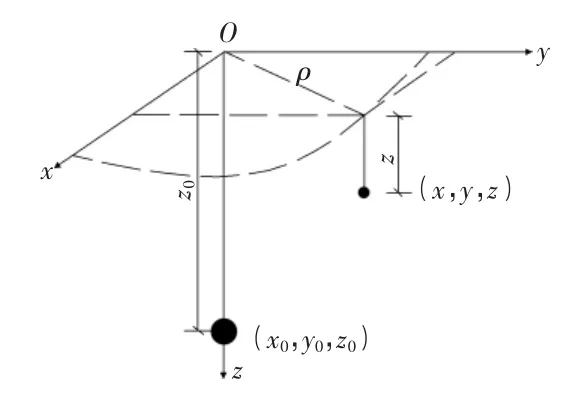
图1 位移计算示意图
问题描述如下:考虑距土体表面深度为h处一点的沉降,其沉降体积在三维问题中为V,在平面应变问题中为每单位长度v(见图1,图2)。为简便起见,计算地面损失量时,沉降点无论是球体还是圆柱体,均取相同的半径a。

图2 位移计算坐标示意图
2.1 无限介质体
如果不考虑土体表面,该问题变成以沉降点为对称中心,由此任何点的位移都是径向的,而其他分量为零。由于体积不可压缩,距沉降点为r处的各点将会产生沿径向向内的位移[1-4]。
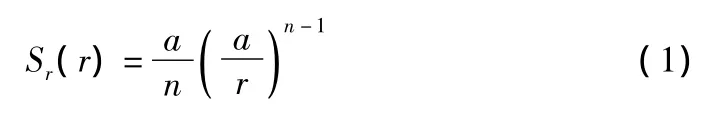
其中,在平面应变分析时n=2,在三维分析时n=3。式(1)导出的前提是小位移情况下,且不考虑几何形变。下面的推导将遵循上面的假设。
在笛卡儿参考系中,如果沉降点坐标为C(x0,y0,z0),任一点P(x,y,z)的位移分量分别为:
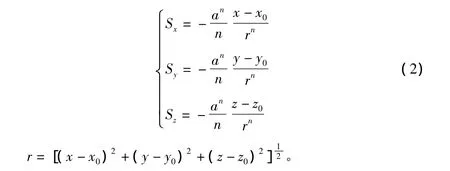
在平面情况下:

2.2 半空间体中沉降镜像点的位移
由于土体的应力—应变特性,式(2)所表示的位移将产生应力场。如果采取前面所述负镜像,半空间体表面将没有垂向正应力,但水平方向剪应力将为原来的两倍(在城市地区由于基坑开挖而引起土体位移分析时采用上面的模型则具有较好的相似性,尤其是要求位移的垂直分量时则更加适合)。把由沉降点及其负镜像点而引起的位移相加,可以得到在xz平面点的位移(其他点的位移可以由平面应变或轴对称情况得出)。


注:式中h与图1中z0意义相同。
利用柱面坐标由式(3)可以直接得出在半无限孔体中,局部土体收缩引起土体中任一点m(x,y,z)的竖向位移和水平位移分别为:
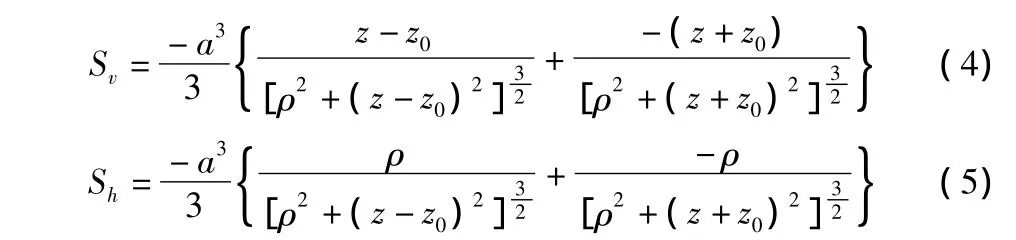
其中,a为小球半径;z0为小球体球心距地表面的垂直距离;ρ为小球体球心距,点的水平距离
2.3 沉桩时土体位移的变化
由于桩以圆柱体居多,我们从中取一微分段dh。对此微分段用一等体积的小球来代替,则等代小球的半径a可由下式求出:
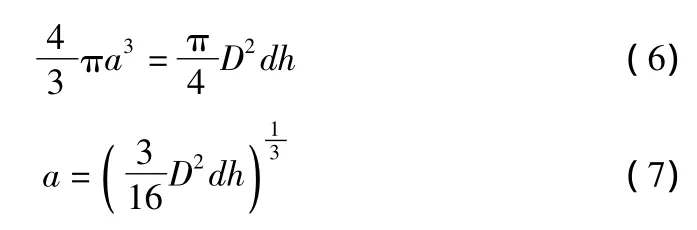
其中,D为桩径。
将式(6),式(7)代入式(4),式(5),就得到该圆柱体微分段引起的任一点位移:
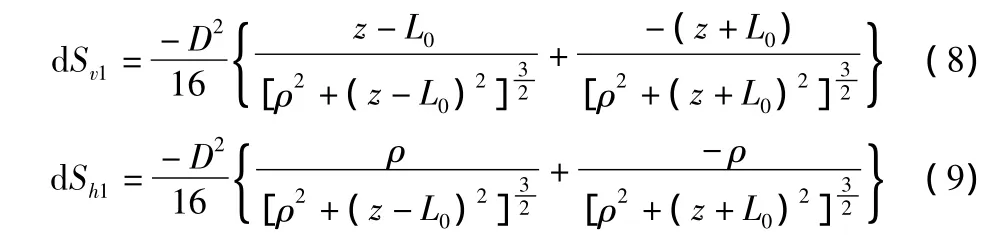
对式(8),式(9)沿整个桩长L0积分就得到由于沉桩而引起的土体的位移为:

在实际工程中,我们更关心的是群桩施工时对土体的挤土效应。同济大学的许福贵教授指出:使用Sagaseta解计算单桩施工引起的土体位移进行矢量叠加之后,尚应计及已经施工的桩对被打桩引起地面位移的削弱作用,并观察统计得出,当计算点位于已施工桩所包围的区域内时,应将单桩计算叠加结果乘以0.6~0.75的系数;当计算点位于已施工桩所包围的区域外时,应将单桩计算叠加结果乘以0.8~0.9的系数。本文的后续计算也采用这一系数来对多桩情况进行修正。
2.4 桩挤土位移的变化规律
由式(10),式(11)编制计算表,计算可得桩挤土在各深度处沿半径的变化值见表1,表2,变化规律见图3,图4。
3 试验实例
试验分3组进行,分别采用不同截面形式木桩压入土体,百分表记录土体位移数据。对试验数据和计算数据进行比较。
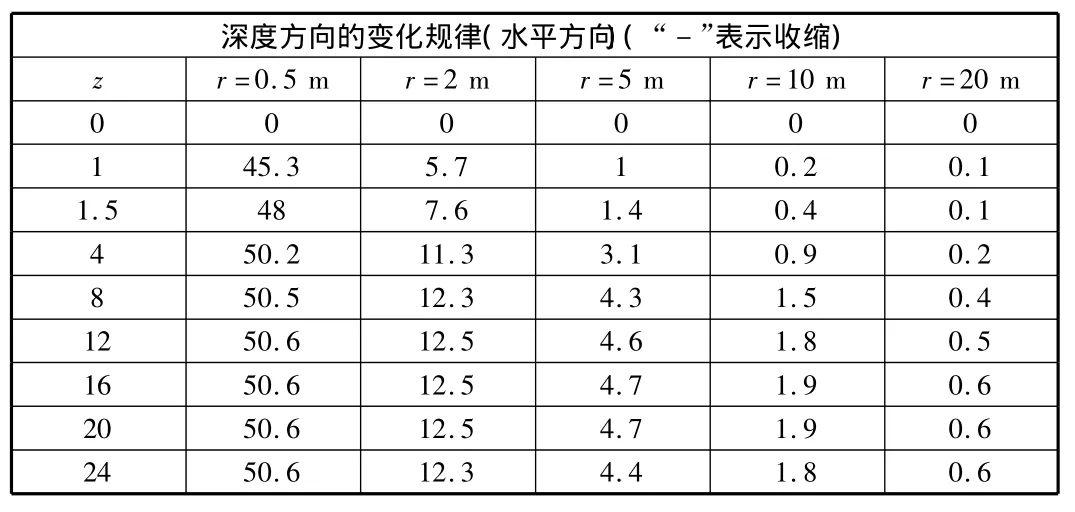
表1 工程桩沿半径方向挤土变化规律(一)
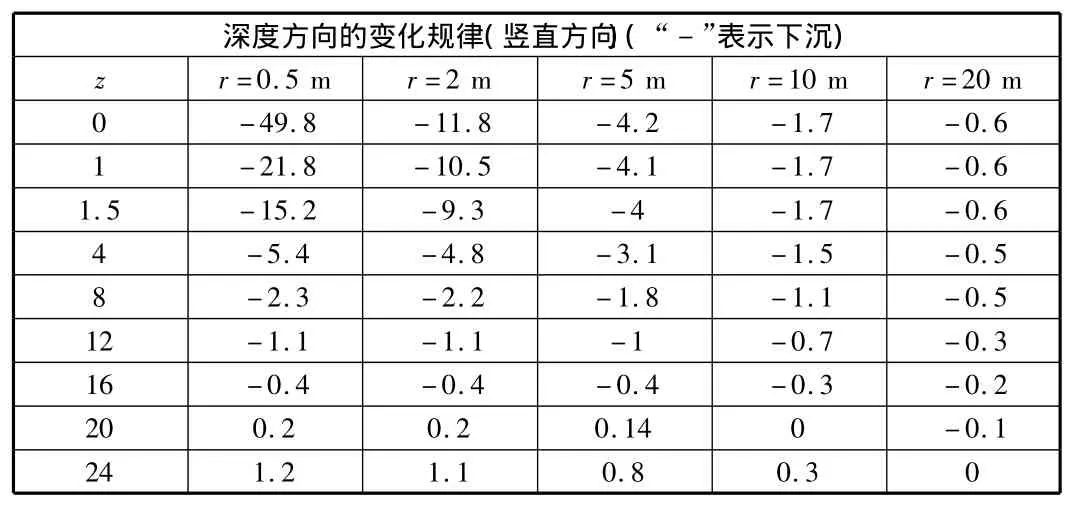
表2 工程桩沿半径方向挤土变化规律(二)

图3 沿半径的挤土变化规律(水平方向)

图4 沿半径的挤土变化规律(竖直方向)
按照试验条件,建立坐标系进行计算,对于试验三中的双桩情况采用矢量叠加得到总位移,见表3(表中“1-js”表示第一组试验计算值,“1-sc”表示第一组试验实测值,以下同)。

表3 计算值和实测值的比较(水平方向)
4 结语
由图5不难看出:
1)对于距离桩截面形心较近处(约10倍桩径)的计算值略大于实测值,计算偏于安全。2)对于大于10倍桩径的较远处,计算值小于实测值,公式有待进一步修正后使用。产生误差的原因主要是公式中忽略了有关土体性质及塑性变形的影响的缘故。
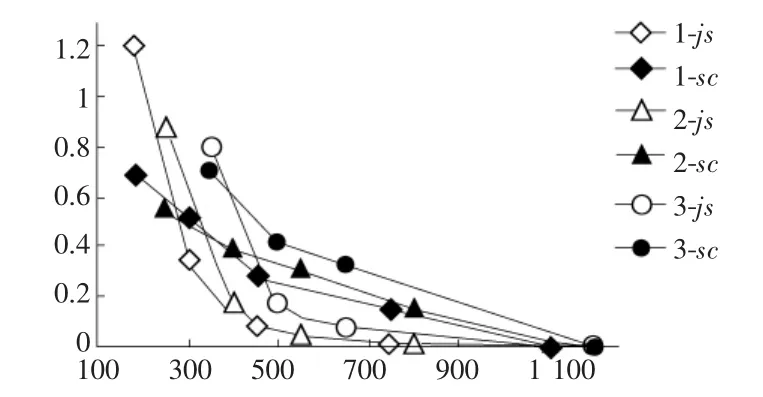
图5 计算值和实测值的比较
由于公式对于10倍桩径范围内的挤土位移的计算是合适的,这对于大多数工程场地条件来说已经够用。加之公式相对简单,没有涉及土体参数,用于适当的现场条件的土体位移计算还是比较适合的。
[1] Sagaseta C.Analysis of undrained soil deformation due to ground loss[J].Geotecechnique,1978,37(3):301-302.
[2] Vesic.A.S.Expansion of Cavity in an infinite Soil Mass,J.S.M.F.ASCE,1972.
[3] 吴家龙.弹性力学[M].上海:同济大学出版社,1993.
[4] 夏志皋.塑性力学[M].上海:同济大学出版社,1991.
[5] 彭 劼,施建勇,黄 刚.考虑挤土效应的桩基承载力分析[J].河海大学学报(自然科学版),2002(28):56-57.
