基于弹簧阻尼模型的共振破碎机碰撞力分析

刘 鹏，李万莉

LIU Peng, LI Wan-li

（同济大学 机械与能源工程学院，上海 201804）

共振破碎机工作时，共振梁输出端锤头与水泥混凝土路面发生接触碰撞，接触力的大小直接影响到路面的破碎效果。根据持续时间的长短可以把接触现象分为静态接触和动态接触[1]。动态接触也叫碰撞，因其作用时间短，碰撞产生的瞬间作用力大，不易进行直接测量和研究，本文选用弹簧阻尼接触模型对共振破碎机的碰撞过程进行研究和分析。

1 接触碰撞数学模型

共振破碎机正常工作时，由安装于共振梁输入端的偏心质量激振器产生驱动，带动共振梁输出端的锤头以一定的频率上下振动。

图1为根据碰撞建立的等效的弹簧阻尼模型示意图，将锤头与路面的接触力等效为一个弹簧阻尼元件进行分析。某时刻t，锤头以速度v向下运动，与水泥路面发生碰撞。

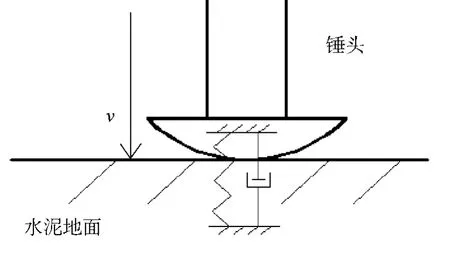
图1 等效弹簧阻尼模型示意图

在上述弹簧阻尼模型中，定义锤头与路面的法向接触力为Fn，表示为[2]

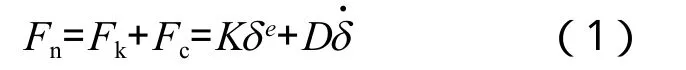
其中，K为Hertz刚度系数，与接触面材料的性质、接触面曲率半径有关，可表示为

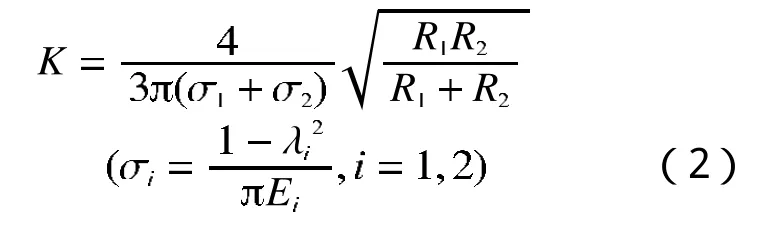
公式(1)中δ表示锤头的法向穿透深度；e为刚性指数，反映了材料的非线性程度，一般取值为表示接触点的法向相对速度，D表示等效的阻尼系数。

公式(2)中Ei和λi分别表示接触物体材料的弹性模量和泊松比，R表示曲率半径(本例中R1表示锤头截面圆的半径，R2为路面接触点的半径，

根据Hund和Grossley的研究，其等效阻尼系数D与恢复系数和刚度系数有关，可表示为[3]

参数μ为迟渧阻尼因子，其一般表达式为

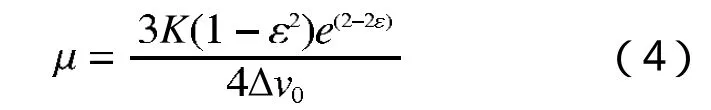
式中ε为牛顿恢复系数，ε＝Δv0/Δvt，为碰撞前相对速度Δv0与碰撞后相对速度Δvt之比。

2 接触力最大值理论计算

锤头－路面碰撞模型的接触力最大值对振动系统的反冲击影响很大，并直接影响到路面的破碎效果，需要重点分析，本节将通过碰撞理论计算接触力的最大值。基于共振破碎机锤头－路面碰撞模型，选择锤头为钢材料，其弹性模量E1＝200GPa，泊松比λ1＝0.3，密度ρ1＝7800kg/m3。

选择路面为水泥混凝土材料，其相关参数为：E2＝ 30GPa，λ2＝ 0.15，ρ2＝ 2400kg/m3。

根据锤头振动时的相关参数：振幅Am＝20mm，频率f＝44Hz，可知锤头的振动方程为

其速度方程为

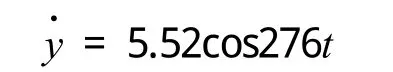
将锤头和水泥混凝土的物理参数代入第1节的计算公式，定义X为锤头振动平衡位置与水泥混凝土路面的竖直距离，

分别计算出当X＝0，5，10，15时最大接触力的理论值，如表1所示。

表1 理论计算数据

3 ADAMS仿真

3.1 仿真模型阻尼系数的确定

利用ADAMS软件进行基于弹簧阻尼模型的接触碰撞仿真时，接触力刚度系数为常量，弹性力部分较易确定；阻尼系数是变量，与碰撞切入深度和物体相对速度有关，难以直接确定，本文采用ADAMS软件提供的STEP函数[4]来模拟阻尼系数

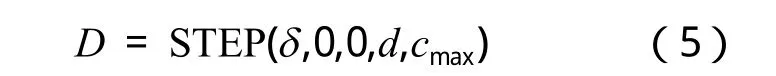
其中，cmax为最大阻尼系数；d为达到最大阻尼系数时的切入深度。

将公式(1)中的阻尼系数D用STEP函数代替，可以得到

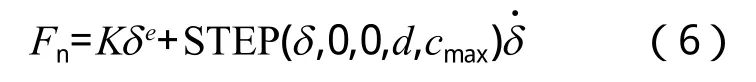
3.2 ADAMS弹簧阻尼模型的仿真

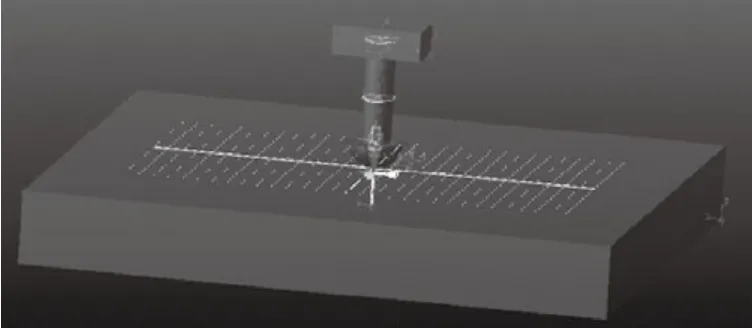
图2 锤头－路面模型图

图2为锤头－路面碰撞三维模型的示意图，定义锤头竖直运动的滑移副，并定义锤头在此滑移副的驱动为

定义锤头为steel材料，输入其弹性模量等参数；在ADAMS模型中没有水泥混凝土材料，需要根据第2节定义其模型及参数，之后根据公路水泥混凝土设计规范，水泥混凝土路面模型长、宽、高尺寸选取为2m、2m、0.25m。

设置仿真时间为5s，仿真步数为1000，分别对X=0,5,10,15进行仿真，因篇幅有限，此处仅给出X=0的仿真曲线，如图3所示。

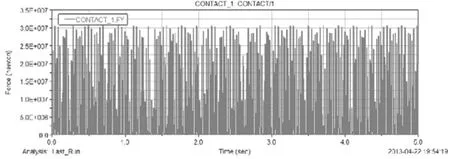
图3 接触力－时间曲线（X=0）

利用ADAMS的后处理模块进行数据统计分析，得到仿真模型的接触力最大值，并与理论值对比计算误差如表2所示。

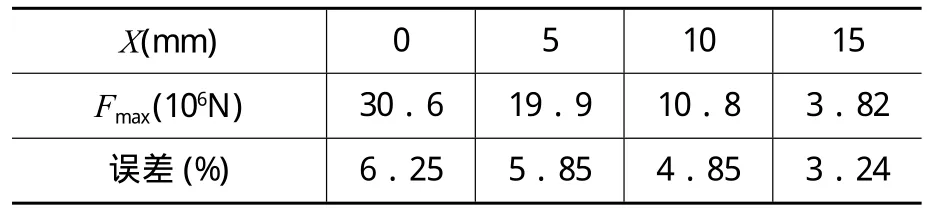
表2 仿真数据及其误差

表2中，Fmax表示接触力的最大值。根据表1和表2，分析可知仿真模型数据和理论计算数据大小和变化规律基本一致，所产生的误差在于ADAMS仿真模型中相关参数的简化，处于合理的范围内，故而所建的ADAMS碰撞模型是正确的。

将仿真得到的接触力数据导入MATLAB进行数据统计分析，可得在时间0～5s内，测得的仿真模型接触力的有效数据数量如表3所示，有效数据越多，则表示锤头与路面接触时间越久，锤头做的有用功越大，路面破碎效果越好。

表3 有效数据数量

由表1、表2数据可得到结论：随着锤头振动平衡位置与水泥混凝土路面垂直距离的增大，二者之间接触力的最大值呈非线性减小；根据表3数据可知：随着此距离的增大，锤头路面碰撞的有效时间减少，锤头的有用功减小。接触力越大，越易破碎路面，但也会产生较大的碰撞反冲击力，容易引起机架及机架支持构件的振动，同时过大的接触力容易破坏路面的路基；若通过提升锤头振动平衡位置来减小接触力，则碰撞的有效作用时间减小，既损失了振动能量，又不利于水泥路面的破碎。

4 结 语

物体之间的碰撞接触力是一种非线性接触力，与两物体的材料性质和运动状态等因素有关。本文基于弹簧阻尼模型建立了共振破碎机锤头—路面接触碰撞的数学模型。之后利用ADAMS软件建立了碰撞的三维模型并进行仿真，仿真得到了接触力最大值随锤头振动平衡位置与水泥混凝土路面距离的变化关系：当距离增大时，接触力最大值呈非线性减小，同时有效碰撞时间减小。在实际施工时，可根据此结论合理选择锤头振动的平衡位置，既达到需求的水泥路面的破碎效果，又可充分利用振动能量，同时避免产生较大的机架振动。

[1]彼得∙艾伯哈特，胡 斌.现代接触动力学[M].南京：东南大学出版社，2003.

[2]周志才,吴新跃,张文群,等.基于弹簧阻尼模型的碰撞动力学研究[J].湖北工业大学学报，2012，27(1)：125-128.

[3]Hami.M.Lankarani.Parvize.Nikravesh.Continuou.Contac.Forc.Model.fo.Impac.Analysi.i.Multibod.Systems[J].Nonlinea.Dynamics.1994,（5)：193-207.

[4]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社，2006.