结构网格方法对高升力构型的应用研究

洪俊武，王运涛，庞宇飞，孟德虹

（1．中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000；2．中国空气动力研究与发展中心 计算空气动力学研究所，四川 绵阳 621000）

0 引 言

对于CFD研究的精细化模拟，结构网格相对非结构网格来说，具有边界层模拟更准确、计算效率更高的优势，因此依然在CFD计算中占据着主流地位。随着计算外形的日益复杂化，传统的多块对接网格已经很难适用于所有外形，因此结构网格又发展出了两种新的形式：重叠网格和拼接网格。这两种网格形式的出现，使得结构网格对于复杂外形具有更强的适应能力，很多原本难以解决的不规则外形，诸如剪刀缝等，可以迎刃而解。重叠网格和拼接网格在交接面均采用一阶插值，从严格意义上来说，会降低局部流场的计算精度；不过大量计算结果表明，合理地选择重叠或者拼接方案，避免在流场变化剧烈的区域插值，会大大降低流场插值所带来的精度损失，并把插值导致的误差控制在工程应用可接受的范围之内；而重叠和拼接技术的合理应用，在降低网格生成难度和减小网格规模方面所带来的收益，相对于插值带来的较小误差来说，是令人满意和振奋的。正因如此，重叠和拼接网格技术在复杂外形计算中得到了十分广泛的应用，本文也对此进行了进一步的综合对比研究。为了体现结构网格精细化模拟的特点，本文选择了某三段式的梯形翼高升力构型进行了数值模拟。

多段二维翼型和三维高升力构型的流场一般与流动分离、转捩和边界层掺混等复杂流动物理现象密切相关。随着计算机硬件技术和CFD技术本身的发展，采用基于雷诺平均NS方程（RANS）的数值模拟软件已经可以模拟真实飞行器的复杂外形及全机的复杂流场［1］，但高升力构型的数值模拟可信度水平依然较低，采用CFD手段尚很难准确模拟高升力构型的最大升力系数及失速迎角，特别是对于存在明显分离区的复杂流动，准确预测分离流动的开始和发展依然是CFD的难点之一。

为了研究高升力构型的流动机理，提高CFD软件的数值模拟精度，空气动力学的试验工作者和CFD工作者付出了巨大的努力［2－5］，高升力构型的数值模拟也是许多CFD可信度专题会议的主题。尽管采用RANS方程模拟高升力构型存在诸多困难，尤其是工程湍流模型的适用范围也众说纷纭，但采用RANS方程和工程湍流模型依然是模拟飞行器复杂构型的主要手段。随着网格生成技术、大规模并行计算技术和工程湍流模型研究工作的不断深入，采用RANS方程模拟高升力构型的可信度水平有望达到一个新的高度。

本文采用的梯形翼模型是为CFD工作者广泛采用的确认算例之一［6－7］，最早是作为简单的后掠翼模型于80年代后期完成设计和实验的，最近的风洞试验是在1998年在NASA Langley 14×22英尺亚声速风洞（FST）和NASA Ames 12英尺增压风洞（PWT）中完成的。FST风洞试验的马赫数为0．2，雷诺数为4．3×106；PWT风洞试验的马赫数为0．15，雷诺数范围为3．4×106～14．7×106，试验的目的就是为CFD软件的验证和确认提供尽可能详尽的试验数据。本文的对比试验值综合采用了FST和PWT风洞的结果，其中气动力的结果由试验人员进行了洞壁干扰修正。

计算中采用了中国空气动力研究与发展中心（CARDC）自行研发的CFD软件平台TRIP（TRIsonic Platform）来数值模拟高升力构型。TRIP软件采用结构网格技术和有限体积方法，具备了完整的对接／重叠／拼接网格的计算能力，同时大量的数值试验表明，TRIP对这三种不同形式的结构网格，均具有良好的模拟精度和求解效率。为了比较三种结构网格形式对高升力构型精细模拟的适用性，本文利用对接／重叠／拼接网格技术对梯形翼高升力外形的全展长和半展长构型进行了对比计算，数值模拟了高升力构型两种布局的三维复杂流场，并给出了总特性和压力分布与试验值的对比，均取得了良好的应用效果。

1 计算方法

控制方程为曲线坐标系下的N－S方程：

上式采用LU－SGS方法进行离散求解；无粘项离散采用MUSCL格式，并利用Roe格式进行通量分裂；粘性项采用中心差分格式进行计算。

计算中，湍流模型采用目前应用较为广泛的SA一方程模型，该模型计算量相对较小，而且具有良好的鲁棒性。为了加快流场收敛速度，本文采用了多重网格技术进行加速求解，除重叠网格外，文中均采用了三重网格进行计算；重叠网格由于受自身性质所限，在挖洞后得到的实际计算区域是一个不规则块，很难应用多重网格，因此计算时采用的是单重网格。另外为了进一步提高流场收敛速度，均采用了低速预处理技术来加速。

本文在计算中采用了并行技术进行加速求解。并行计算采用域分解法进行数据划分，并使用基于消息传递的并行编程模型，设计开发并行计算模块，采用MPI消息传递库，通过显式地发送和接收消息来完成各处理器之间的数据交换。消息传递方式的并行属于粗粒度并行，具有较好的通用性和可移植性，可以获得较高的并行效率。实际计算中采用了8～32个CPU进行并行运算。

2 计算构型与外形参数

该高升力构型是安装在机身上的大弦长、半展、三段构型。机翼没有扭转、没有上反角，采用大弦长（MAC＝39．6″）和相对较小展弦比（AR＝4．56）构型的目的是获得较高的雷诺数并可以采用压力传感仪器测量边界层厚度［8］。针对梯形翼，设计了两种襟翼构型，一种为“全展长襟翼”，单缝襟翼从翼梢一直延伸到翼根，并融于机身；另一种为“半展长襟翼”，襟翼的展长大约占模型展长的1／2，并置于机翼的中间位置。以上两种襟翼构型具有相同的前缘缝翼，缝翼从翼梢一直延伸到翼根，并融于机身。

图1 梯形高升力模型在PWT风洞中的安装照片Fig．1 The install picture of trap wing high－lift configuration in PWT tunnel

3 对接网格计算全展长襟翼高升力构型

全展长襟翼高升力构型的前缘缝翼与后缘襟翼的偏角分别为30°和25°。本文采用商业软件生成多块对接网格，网格规模达到了1094万，共分为136个网格块，壁面第一层网格距离为0．02mm。计算外形与典型截面网格示意图见图2。

图2 全展长襟翼梯形高升力计算构型网格图Fig．2 Computational grid of full span configuration

图3给出了全展长襟翼高升力构型的升力系数、阻力系数与相应试验结果的比较，其中试验结果经过了洞壁干扰修正（本文所有附图中试验值均为离散点，计算值为连线）。可以看出，在本文的计算范围内，升力、阻力系数均与修正后的试验数据吻合良好。在20°迎角前，升力和阻力与试验值几乎重合，大迎角时计算值均略小，这可能和大迎角时湍流模型的局限性有关。

图3 全展长襟翼梯形高升力构型气动力系数与试验的比较Fig．3 The aerodynamic coefficient of computation vs．experimental results

图4 ～图5给出了M＝0．15，Re＝1．5×107，α＝20．02°时，展向50%站位和85%站位上的压力分布与PWT风洞试验结果的比较，20．02°时已经接近失速迎角。从图中可以看到在前缘缝翼的50%站位上，计算与试验在定性上吻合，而前缘缝翼定量上有一定差别；85%站位无论是主翼，还是前缘缝翼或后缘襟翼上的压力分布在定性与定量两个方面均与试验结果吻合良好。

图4 全展长襟翼梯形高升力典型站位Cp分布（α＝20．02°，y／b＝0．50）Fig．4 The Cpdistribution on typical section（α＝20．02°，y／b＝0．50）

图5 全展长襟翼梯形高升力典型站位Cp分布（α＝20．02°，y／b＝0．85）Fig．5 The Cpdistribution on typical section（α＝20．02°，y／b＝0．85）

需要说明的是，由于高升力构型在缝翼和襟翼打开并偏转后，试验模型的测压点弦向位置会发生变化；而PWT风洞给出的测压数据是按缝翼和襟翼收回位置给出的，与计算结果实际截取位置存在一定差异；同时其测压数据未做修正，中间有若干明显跳点。而FST风洞也提供了一组全展长构型的测压试验值，该结果按照缝翼、襟翼打开／收回的状态均给出对应坐标，并严格说明了试验测压点的截面位置，同时剔除了部分跳点，具有更高的准确度。于是，本文按照FST的试验状态也进行了对比计算，图6～图7给出了M＝0．2，Re＝4．3×106，α＝19．19°时，计算结果展向50%站位和85%站位上的压力分布与FST试验结果的比较。可以看到，本文计算结果与FST的吻合度更高，无论在50%还是85%截面位置，两者都接近重合。由于在其它迎角下，计算值与两个风洞的对比规律都比较类似，即：本文结果与FST相比吻合度很高，而与PWT相比50%站位前襟上翼面Cp均略小，因此本文认为前襟上的差异可能是PWT结果中不同的弦向取值位置造成的。

图6 全展长襟翼梯形高升力典型站位Cp分布（α＝19．19°，y／b＝0．50）Fig．6 The Cpdistribution on typical section（α＝19．19°，y／b＝0．50）

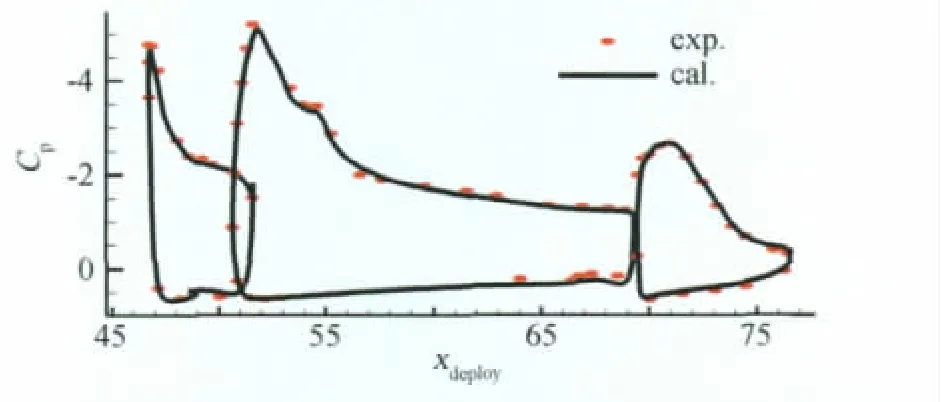
图7 全展长襟翼梯形高升力典型站位Cp分布（α＝19．19°，y／b＝0．85）Fig．7 The Cpdistribution on typical section（α＝19．19°，y／b＝0．85）

4 重叠网格计算全展长襟翼高升力构型

为了比较重叠网格和对接网格的差异，本文采用重叠网格技术对全展长构型重新进行了对比计算。同时，为了研究不同重叠方案带来的计算差异，本文采用了两种不同的重叠方案来对比。

对此类三段式机翼，最常见的重叠思路是将前缘缝翼、主翼和后缘襟翼分为三套网格，这样不仅网格结构简单明了，而且当前翼和后翼偏角改变后也无需重新生成网格，只需将前后两套网格旋转一个角度即可。本文首先按照这种方案生成了一套重叠网格，共三个部件，其中机身和主翼生成一套主网格，前翼和后翼各为一套子网格，分别从主网格中挖洞。计算单元为1200万，壁面第一层网格距离为0．02mm，与对接网格相同。图8给出了该重叠方案下的表面网格和局部示意图。

图8 全展长襟翼高升力构型重叠方案1网格图Fig．8 Computational grid of full span high－lift configuration in overlap scheme 1

图9 给出了利用该重叠方案计算得到的升力系数和阻力系数与对接计算结果和试验结果的比较，图中patch为对接网格，overlap为重叠网格。从图中明显看到，该方案下的计算结果是令人失望的，与对接网格相比，该结果和试验值的吻合程度大幅降低，尤其在大迎角情况下，差异非常大，到了无法接受的地步。

本文认为，造成这种误差的结果在于重叠方案的不合理。图10给出了前后襟翼挖洞后的洞内点集合，可以看到，前后翼的洞内点集合与主翼前后缘非常接近，实际计算中，作为插值的洞边界还要向外延伸两排点，这就使得前后翼的洞边界在插值的时候，不可避免地要从主翼前后缘的附近，也就是主翼和前缘缝翼、后缘襟翼之间的缝隙中去插值。众所周知，对于多段机翼来说，前后缘的缝隙流动能否模拟准确是非常关键的，这两个区域的缝隙流动模拟不好，对紧随其后的主翼和后缘襟翼存在着巨大影响。采用这种重叠网格方案，由于无法避免在缝隙中插值，而且缝隙中的插值网格与被取值的物面附近单元往往体积差异很大造成插值精度降低，因此引入的误差在主翼和襟翼上被充分体现，从而导致了计算结果的较大误差。当计算迎角不太大时（小于15°），缝隙内流场相对来说变化不太剧烈，因此其计算结果与试验值差量还不算大；但是随着迎角的进一步增大，流场变化加剧，结果差异就无法令人接受了。上述计算结果表明，对于此类高升力构型来说，简单地将前后翼剥离出来重叠的方案是不够合理的，尤其大迎角情况下，其计算精度很难让人满意。

图9 全展长高升力构型重叠方案1气动力系数与试验的比较Fig．9 The aerodynamic coefficient of overlap scheme 1vs．experimental results

图10 全展长高升力构型重叠方案1的洞内点显示Fig．10 Collection of hole point in full span high－lift configuration

为此，本文重新制定了一种重叠网格方案。全机只分为两个部件，机身和机翼（包括缝翼和襟翼），主翼和前后翼之间是完全对接的。网格规模与对接网格十分接近，计算单元为1053万，不过由于采用了重叠网格技术，拓扑结构相对简单很多，只有66个网格块；壁面距离和边界层内网格伸展率与对接网格也完全相同。计算外形与重叠示意图见图11。

图11 全展长襟翼高升力构型重叠方案2网格图Fig．11 Computational grid of full span high－lift configuration in overlap scheme 2

图12 给出了利用该重叠方案计算的全展长构型的气动特性与对接计算结果和试验结果的比较。图中可以看到，该方案结果与前述方案有着很大好转，在计算范围内，升力系数、阻力系数均与对接网格结果非常接近，其中升力和阻力在大部分迎角下与对接网格几乎重合，在大迎角下重叠网格得到的升力和阻力与对接网格相比均略小，与试验值的差距稍大，但是这个差距是十分细微的。总体来说，该重叠方案下的计算结果与试验值也吻合的相当好。对比两种不同重叠方案的较大差异，本文认为，对于重叠网格技术来说，其使用起来具有很大的灵活性，这是它的优点之一；但从另一方面来看，这同时意味着用户使用的随意性也会增大。如何合理地选择分块策略，既能保证流场计算精度，又不丧失重叠网格技术带来的便利，需要使用者积累更多的经验。

图13给出了M＝0．2，Re＝4．3×106，α＝19．19°时，该重叠方案结果（三角形连线）展向50%站位上的压力分布与对接网格和FST风洞试验结果的比较。可以看到在两个站位上，重叠网格得到的Cp分布和对接网格基本完全相同，几乎没有可见的差异。从图中也可以清晰地看到，两种计算结果与试验值均吻合的很好，在所有特征点上的量值都是一致的。这也充分证明了本文第二种重叠方案的合理性，虽然该方案与第一种相比，在网格生成的工作量方面有所增加，但是由于这种方案避开了在流场变化剧烈区域插值，因此获得了和对接网格几乎相同的计算精度。

图12 全展长高升力构型气重叠方案2气动力系数与试验的比较Fig．12 The aerodynamic coefficient of overlap scheme 2vs．experimental results

图13 全展长高升力构型重叠方案2典型站位Cp分布（α＝19．19°，y／b＝0．50）Fig．13 The Cpdistribution on typical section（α＝19．19°，y／b＝0．50）

5 拼接网格计算半展长襟翼高升力构型

为了进一步研究结构网格对高升力构型的应用，本文采用拼接网格技术模拟了半展长襟翼高升力构型。半展长高升力构型的前缘缝翼与后缘襟翼的偏角也分别为30°和25°，与全展长完全相同；后缘襟翼的展向长度大约是机翼展长的一半。本文采用商业软件生成多块拼接网格，在后缘襟翼的剪刀缝处采用拼接技术处理，有助于准确模拟剪刀缝，提高网格质量并有效降低网格规模和网格生成难度。模拟该构型的网格规模达到了1081万，共分为158个网格块，壁面距离和边界层内网格伸展率与对接网格也完全相同。该套网格是在全展长构型网格基础上，采用拼接技术修改生成的。计算外形与典型截面网格示意图见图14。

图14 半展长襟翼梯形高升力计算构型网格图Fig．14 Computational grid of part span configuration

值得提出的是，对于半展长构型，由于拼接技术的成功运用，同等密度网格的规模比全展长构型的对接网格还要略少；这是因为虽然剪刀缝处增加了不少网格单元，但是由于襟翼偏转部分的缝隙中网格密度很高，而半展长构型偏转部分的长度只有全展长的一半，所以相对全展长构型来说反而整体网格规模有所降低。

另外，对于拼接网格来说，同样存在着与重叠网格类似的流场插值问题。本文的重叠网格采用了被广泛应用的三线性插值，而拼接网格采用的是面积加权的线性插值。虽然两者的精度都是一阶，但是由于拼接网格中存在着公共面，因此能够实现公共面的通量守恒。对于拼接网格技术来说，同样也需要避开流场剧烈变化区域的插值，然而对剪刀缝问题，在襟翼两侧插值是无法避免的，不过由于襟翼两侧的拼接插值不在主流方向，因此产生的误差并不会对全机流场产生明显影响。对比重叠网格来说，拼接网格由于在拼接块之间存在公共面，虽然在网格生成过程中会增加工作量，但是同时也使得相邻拼接单元尺寸容易控制，有利于保证插值精度。

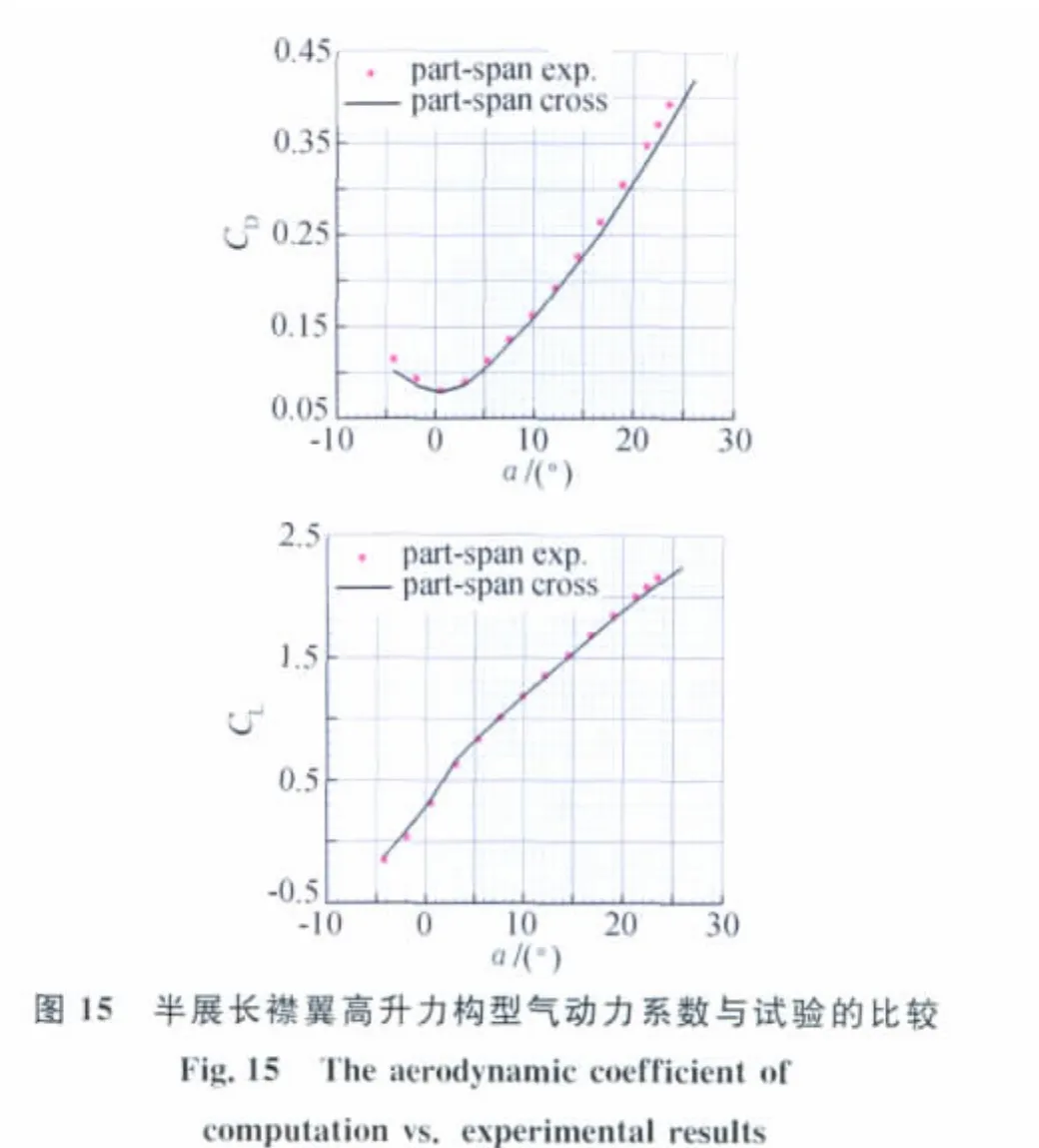
图15给出了利用拼接网格计算的半展长襟翼构型的气动特性与相应试验结果的比较。其中试验结果也经过了洞壁干扰修正。同样可以看出，在本文的计算范围内，拼接网格得到的升力系数、阻力系数仍然与修正后试验数据吻合良好。

图16和图17给出了M＝0．15，Re＝1．5×107，α＝22．33°时，展向50%站位和85%站位上的压力分布与PWT风洞试验结果的比较，其中50%站位位于后缘襟翼偏转部分。该迎角与失速迎角更加接近，计算更具挑战性。可以看到在85%的站位上，缝翼和主翼上的压力分布在定性与定量两个方面均与试验结果吻合良好，包括上表面的压力峰值；而在50%站位上的模拟结果与前述的全展长对比结果类似，也是主翼和后襟吻合，前襟上翼面的计算值略偏小，本文认为这可能与试验值给出的位置差异有关；由于FST风洞并未提供该构型的测压结果，因此本文无法对该构型做进一步比较。不过现有的结果也表明，对高升力构型，利用拼接网格技术得到的无论气动力系数还是Cp分布，都与试验值高度吻合；这也充分说明，本软件的拼接网格技术是成熟可靠的，对此类外形完全可以适用。同时，由于本文的拼接方案，在流向上避开了缝隙内插值，因此后缘襟翼虽然采用拼接技术处理，但是其Cp分布几乎没有引入明显的插值误差：如果忽略试验数据中较为明显的跳点，可以认为后襟Cp分布的计算结果与试验值是非常吻合的。

6 结 论

本文采用TRIP软件和对接／重叠／拼接网格技术，通过求解任意坐标系下的RANS方程，数值模拟了梯形翼高升力构型全展长襟翼与半展长襟翼的三维复杂流场。通过与试验结果相比较，得到以下结论：

（1）目前的CFD结构网格方法对于典型高升力构型具有良好的适用性，在失速迎角前具有令人满意的计算精度；与修正后的试验数据相比，本文数值模拟得到的失速迎角前的气动力系数和典型剖面的压力分布均与试验结果吻合良好；

（2）合理地应用重叠／拼接网格技术，可以在大大降低网格生成工作量的同时，获得与对接网格非常接近的计算精度，本文研究表明，结构网格技术在类高升力构型精细化模拟方面的应用前景是非常广阔的。

［1］ TINOCO E N，BOGUE D R．Progress toward CFD for full flight envelope［J］．Aeronautical Jounal，2005，109：451－460．

［2］ PAUL L．JOHNSON，KENNETH M．JONES，MICHAEL D．MADSON．Experimental investigation of a simplified 3Dhigh lift configuration in support of CFD validation［R］．AIAA 2000－4217．

［3］ STUART E．ROGERS，KARLIN ROTH，STEVEN M．NASH．CFD validation of high－lift flows with significant wind－tunnel effects［R］．AIAA 2000－4218．

［4］ CHRISTOPHER L．RUMSEY，THOMAS B．GATSKI，SUSAN X．YING，et al．Prediction of high－lift flows using turbulent closure models［R］．AIAA－97－2260．

［5］ 朱自强，陈迎春，吴宗成，等．高升力系统外形的数值模拟计算［J］．航空学报，2005，26（3）：257－262．

［6］ CHRISTOPHER L．RUMSEY，SUSAN X．YING．Prediction of high lift：review of present CFD capability［J］．Progress in Aerospace Sciences，2002，38：145－180．

［7］ CHRISTOPHER L．RUMSEY，THOMAS B．GATSKI，SUSAN X．YING et al．Prediction of high－lift flows using turbulent closure models［R］．AIAA－97－2260．

［8］ STUART E．ROGERS，KARLIN ROTH，CFD validation of high－lift flows with significant wind－tunnel effects［R］．AIAA－2000－4218．