垂直扬矿管道堵塞条件下的水力特性

曹 斌，夏建新，刘 鑫

(中央民族大学生命与环境科学学院，北京 100081)

深海蕴藏着丰富的多金属结核、多金属硫化物以及富钴结壳等矿产资源，进行深海采矿时，位于深海底的这些固体矿物需要通过垂直扬矿管道(以下简称垂直管道)提升到海面采矿船上。由于细颗粒难以脱水或物料粉碎困难等原因，经过初步破碎进入垂直管道的固体矿物一般颗粒较粗，最大颗粒直径可达20 mm。目前，学者对深海垂直管道输送技术开展了大量研究［1-6］，不同学者从不同角度对垂直管道中的颗粒输送速度进行了研究，并得到一些经验公式，如姜龙等［7］基于一个静止颗粒在垂直输送管道中起动时的受力平衡及试验分析推导了垂直管道水力提升临界淤堵流速的半理论半经验公式;金文斌等［8］利用一种新的试验方法测定颗粒在垂直管道内的浮游速度，并利用测定的浮游速度确定大颗粒在垂直管道内的最小输送速度，给出了一定颗粒粒级和体积浓度范围的最小输送速度的经验计算公式。

然而，当垂直管道面对恶劣的工作条件时，管道堵塞的风险极大，而目前针对管道堵塞的研究较少。陈光国等［9］进行了单颗粒群、均匀颗粒群和非均匀颗粒群3种沉降试验，分析了颗粒体积分数、级配、粒径、边界条件等因素对颗粒及颗粒群沉降速度的影响，对粗颗粒在垂直管道中的沉降运动规律进行了探索。因此，了解垂直管道堵塞状况下的水力特性，不仅可以提前预测堵塞风险，还可以为堵管后制定应急决策提供依据。

笔者利用垂直管道输送试验系统，研究粗颗粒在垂直管道中发生堵管后，堵管高度H、单位长度的压差ΔP、颗粒粒径d与流体平均流速V之间的变化规律，提出垂直管道堵塞条件下的应急措施。

1 垂直管道输送试验系统及方法

图1 管道水力输送试验系统示意图Fig.1 Schematic diagram of experimental system of hydraulic transportation

试验系统由涡流泵、有机玻璃管道、稳压水箱等组成(图1)。有机玻璃管道内径为25mm，长度为2.0 m，在垂直有机玻璃管上等距离取4个测压点，安装高精度数字压力计A，B，C，D自下而上测量两点间的ΔP，分别用ΔP1，ΔP2，ΔP3，ΔP4表示。在试验系统控制与测量方面，涡流泵采用变频调速器进行无级调速，确保满足试验所需的流体输送速度和颗粒体积分数。试验液相为清水，固相为天然石英砂，粒径分为0.8～1.0 mm，1.0～2.0 mm，2.0～3.0 mm，3.0～4.0 mm，4.0～5.0 mm共5组;每组粒径按照H分别为1.0 m，1.3 m，1.5 m，1.8 m，2.0 m进行试验。

试验时，先按照设定的H将粗颗粒填充到垂直有机玻璃管中每两个测压点中点处，然后起动涡流泵，涡流泵转速由变频调速器控制，由低到高逐级加速。试验中，观察不同H、不同d条件下ΔP与V之间的关系，固液两相流的平均流速可以通过在管道出口取样标定得到。

2 垂直管道堵塞时ΔP的影响因素

管道阻力损失是粗颗粒长距离管道水力输送的重要参数之一，其关系到动力设备的选择和运行能耗。影响管道阻力损失的因素众多，主要因素有H，d，V等。

2.1 d与ΔP的关系

图2为H一定时，粗颗粒再起动时ΔP与V的关系。试验研究发现，粗颗粒堵管再起动时，d对ΔP和V存在较明显的影响，且ΔP与V存在3种关系。

图2 不同d条件下ΔP与V的关系Fig.2 Relationship between average flow velocity and pressure gradient under condition of different particle sizes

H=2.0 m时，由于垂直管道处于堵塞状态，粗颗粒呈静止状态，水流通过颗粒间的孔隙流动，类似于渗流，ΔP与V呈线性关系，即V随着ΔP的增加而增加，符合达西定理。如d=2.0～3.0 mm时，当ΔP从6.08 kPa/m逐渐增加到21.67 kPa/m时，管道中流体的V从0.10 m/s逐渐增加到0.48 m/s。

H=1.8 m时，ΔP与V间存在2种关系:(a)d=4.0～5.0 mm时，由于管道呈堵塞状态，管道中的粗颗粒呈静止状态，ΔP与V呈线性关系，如ΔP从2.84 kPa/m逐渐增加到13.93 kPa/m时，V从0.27 m/s逐渐增加到0.80m/s。(b)d＜4.0mm时，随着V的增加，颗粒自上而下逐渐起动，渗流稳定性被破坏，此时ΔP与V呈非线性关系，即当ΔP＜10.79kPa/m时，V随ΔP的增加变化较小;当ΔP≥10.79kPa/m，V随着ΔP的增加迅速增加，且d越大，增加的趋势越明显，由于垂直管道中的粗颗粒自上层开始逐渐运动，ΔP的变化趋势逐渐趋于稳定。

H=1.5 m时，ΔP与V呈现非线性关系，且d越大，非线性关系越明显。当d＜2.0 mm时，随着ΔP的增加V变化较小。ΔP＜2.94 kPa/m时，V＜0.25 m/s，此时管道中的粗颗粒以颗粒群的形式自上而下逐渐起动;当d≥2.0 mm时，V随ΔP的变化趋势与H=1.8 m时类似，不再赘述。

ΔP相同时，随着d的增大，V逐渐增加，如H=2.0 m，ΔP=9.81 kPa/m时，随着d的增大，V由0.07 m/s增加到0.42 m/s。这是由于随着d增加，颗粒间的孔隙率变大，因此管道中V变大。

2.2 H与ΔP的关系

图3为不同H对应的ΔP与V的关系。由图3可知，无论d如何变化，H一定时，ΔP与V呈线性关系;d一定时，随着H的增大，ΔP所导致的管道中V越小。

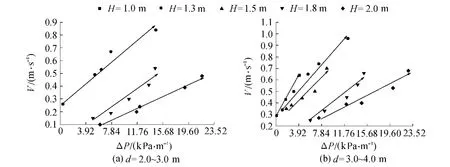
图3 不同H条件下ΔP与V的关系nship between average flow velocity and pressure gradient under condition of different heights of pipeline jam

对粗颗粒而言，随着H的增加，垂直管道中的阻力损失越大，其占总阻力损失的比例也越大，水流紊动能量中用于支持颗粒悬浮的能耗也增加。因此，在d和ΔP都一定时管道中的V越小。

由图2可知，d≥4.0 mm且H＞1.8 m时，系统将无法提供足够的动力以实现再起动，ΔP与V呈线性关系;而当H＞2.0 m时，无论d如何变化颗粒均无法再起动，此时ΔP与V呈线性关系。在本文试验条件下，若要实现垂直管道堵塞后颗粒再起动，对于d≥4.0 mm的颗粒，需要使H＜1.8 m;对于d＜4.0 mm的颗粒，应H＜2.0 m，ΔP与V呈非线性关系，且当ΔP增加到一个最大值后，颗粒上层开始运动，然后ΔP趋于稳定。

3 堵管后粗颗粒再起动的临界条件

垂直管道内粗颗粒堵管后再起动的临界条件是进行管道安全输送的关键问题。本文所指的临界条件是粗颗粒在垂直管道中由静止状态向运动状态转变时的条件，一般用临界平均流速V临界和临界单位长度压差ΔP临界表征。

3.1 堵管后粗颗粒再起动的临界平均流速

当垂直管道发生堵塞后，粗颗粒再起动需要逐步加大V，随着V的增大，颗粒间由密实状态逐渐向松动状态转变，且由最上层单颗粒起动向颗粒群起动转变。当颗粒群达到一定数量时，垂直管道中的颗粒将在短时间内迅速实现再起动。H一定时，d越大则颗粒再起动所需的V越大;d一定时，H越高则颗粒再起动时所需的V越大。d相同时，H越高则颗粒的数量越多，颗粒在管道中的有效重力越大，颗粒与管壁间的摩擦力越大，颗粒间的相互影响也越大，颗粒再起动所需要的流体拖曳力就越大，所需要的V也越大。H相同时，d越大则颗粒再起动时所需要的V越大，原因在于随着d的增加，颗粒间作用力、颗粒和管壁间的作用力更容易使颗粒形成料栓导致堵管。

通过2.2节分析可知，对于d≥4.0 mm的颗粒，H=1.8 m是其临界堵管高度，而对于d＜4.0 mm的颗粒，H=2.0 m是其临界堵管高度。且d一定时，H越高，其临界单位长度压差、临界平均流速越大;H一定时，d越大，对应的临界单位长度压差、临界平均流速越大;但是d越大，H越高，临界单位长度压差的变化越小。

目前，国内外在试验及分析基础上提出很多计算临界平均流速的公式，但一般可转化为［10］

式中:Vc——临界平均流速;g——重力加速度;D——管径;Cv——颗粒体积分数;S——颗粒相对密度;ρs——颗粒密度;ρ0——清水密度。

试验结果表明，垂直管道堵管后粗颗粒再起动的Vc与D，d，H密切相关(图4)。因此，式(1)可转化为

式中K为表征颗粒形状因素等的修正系数，本文取为0.12。

图4 不同条件下粗颗粒再起动的临界平均流速Fig.4 Critical average flow velocity of re-initiation of particle motion under conditions of different heights of pipeline jam and particle sizes

3.2 粗颗粒再起动时临界单位长度压差

堵管后要达到粗颗粒再起动的Vc，必须加大堵管段的ΔP。临界单位长度压差与Vc类似，其也与d/D，D/H以及S等参数相关。

夏建新等［11］的研究表明固液两相流在垂直管道中运动时ΔP主要由两部分组成:

式中:ΔPf——载体与管壁的摩擦损失;ΔPs——提升粗颗粒的位能损失(见文献［12］);λf——流体摩阻系数;v——水流速度;Δ/D——管道相对粗糙度，约为0.0011;Re——雷诺数;K'——与颗粒粒径、颗粒体积分数、平均流速、管径以及浆体密度等有关的参数(图5)。

利用量纲分析法可得

式中k为修正系数，根据本文试验条件取为2.0×10-7。

图6分别为Vc以及临界单位长度压差的计算值与实测值的比较，可看出二者基本吻合。

5 结 论

a.d一定时，d对ΔP与V的关系存在较明显的影响。其中当d=4.0～5.0 mm，H＞1.5 m时，ΔP与V呈线性关系，此时管道系统中的颗粒呈现静止状态;当d为0.8～1.0 mm，1.0～2.0 mm，2.0～3.0 mm，3.0～4.0 mm、H＜1.8 m时，ΔP与V呈非线性关系，此时管道系统的颗粒可通过提高V的方法实现系统的再起动。

b.针对不同粒径的颗粒，ΔP相同的条件下，随着d的增大，管道中V逐渐增加，这是由于随着d增加，颗粒间的孔隙率变大，则管道中V变大。

图5 不同条件下粗颗粒再起动的临界单位长度压差ig.5 Critical pressure gradient for re-initiation of particle motion under different conditions

图6 临界平均流速与临界单位长度压差实测值与计算值的比较Comparison of measured and calculated critical average flow velocity and critical pressure gradient

c.H是影响ΔP与V关系的另一个重要因素。H一定时，ΔP与V呈线性关系;相同d条件下，随着H的增大，ΔP所导致的管道中V越小。

d.当H一定时，d越大，其单位长度的临界压差也越大，临界平均流速亦增大。但是d越大，H越高，单位长度的临界压差的变化越小。

e.基于试验结果，提出了粗颗粒在垂直管道实现再起动时临界流速和单位长度的临界压差计算公式，可为管道输送系统参数设计提供依据。

［1］唐军，黄艳国，李辉.深海采矿水力提升系统动力学建模［J］.矿山机械，2010，38(5):11-13.(TANGJun，HUANG Yanguo，LI Hui.Dynamic model of the hydraulic lifting system for deep ocean mining［J］.Mining＆Processing Equipment，2010，38(5):11-13.(in Chinese))

［2］毛纪陵，申焱华，凌胜.深海采矿扬矿管工艺参数的模拟研究［J］.有色金属:矿山部分，2000(5):22-25，37.(MAO Jiling，SHEN Yanhua，LING Sheng.The simulation study of technological parameters on lifting-mine pipe of deep-ocean mining［J］.Nonferrous Metals:Mining Section，2000(5):22-25，37.(in Chinese))

［3］夏建新，倪晋仁，黄家桢.粗颗粒物料在垂直管流中的滞留效应［J］.矿冶工程，2002，22(3):37-40.(XIA Jianxin，NI Jinren，HUANG Jiazhen.Lagging effect of coarse materials in vertical pipe flow［J］.Mining Metallurgical Engineering，2002，22(3):37-40.(in Chinese))

［4］赵国景，夏建新，黄家桢.锰结核动态管道水力提升［J］.矿冶工程，2000，20(3):18-20，24.(ZHAO Guojing，XIA Jianxin，HUANG Jiazhen.Hydraulic lift of dynamic pipelines for manganesenodules［J］.Mining Metallurgical Engineering，2000，20(3):18-20，24.(in Chinese))

［5］韩凝，夏建新.深海采矿水力提升管路系统紧急泄料过程参数分析［J］.金属矿山，2008(10):35-38.(HAN Ning，XIA Jianxin.Analysis of the process parameters of the hydraulic lifting piping system in deep-sea mining［J］.Metalmine，2008(10):35-38.(in Chinese))

［6］林愉，唐军.深海采矿水力提升系统经济流速的研究［J］.西部探矿工程，2006，18(9):72-74.(LIN Yu，TANG Jun.The research of economic velocity on hydraulic hoisting system of deep-sea mining［J］.West-China Exploration Engineering，2006，18(9):72-74(in Chinese))

［7］姜龙，李鹏程，田龙，等.垂直管水力提升临界淤堵流速的实验［J］.有色金属，2006，58(1):82-85.(JIANG Long，LI Pengcheng，TIANLong，et al.Experiment on critical velocity in vertical pipes for hydraulic lifting［J］.Nonferrous Metals，2006，58(1):82-85.(in Chinese))

［8］金文斌，黄小平，高文鹏.大颗粒物料在垂直管道内最小输送速度的试验研究［J］.矿业研究与开发，1997，17(2):17-20.(JIN Wenbin，HUANG Xiaoping，GAO Wenpeng.An experimental study on minmal transporting velocity of the lifted large-size particle material in vertical piping［J］.Mining Research and Development，1997，17(2):17-20.(in Chinese))

［9］陈光国，阳宁，唐达生，等.垂直管道颗粒及颗粒群沉降运动规律研究［J］.泥沙研究，2010(4):16-21.(CHEN Guangguo，YANG Ning，TANG Dasheng，et al.Study on the settling regularity of solid particles in vertical pipelines［J］.Journal of Sediment Research，2010(4):16-21.(in Chinese))

［10］费俊祥.浆体与粒状物料输送水力学［M］.北京:清华大学出版社，1994.

［11］夏建新，倪晋仁，黄家桢.锰结核在垂直管路输送过程中的压力损失［J］.泥沙研究，2002(2):23-28.(XIA Jianxin，NI Jinren，HUANG Jiazhen.Pressure loss in solid-liquid flow with coarse manganese nodules invertical pipeline［J］.Journal of Sediment Research，2002(2):23-28.(in Chinese))

［12］孙凯年，刘可任，章庆松.液固两相流垂直管道向上输送水力坡度的研究［J］.黄金，1987(2):4-7.(SUN Kainian，LIU Keren，ZHANG Qingsong.The research of hydraulic gradient in the vertical upward transportation pipeline for solid-liquid flow［J］.Gold，1987(2):4-7.(in Chinese))