Rogowski线圈电流互感器相差分析与补偿研究

王 奕，邓忠华，霍伟文

（1.广东电网公司，广东 广州 510080；2.广东中钰科技有限公司，广东 广州 511495）

0 引言

电流互感器是电力系统中电能计量和继电保护设备所依赖的重要信号来源，在新兴的数字化变电站中占有举足轻重的地位[1]。随着我国电力工业的迅速发展，电力传输系统容量不断增加，传统的电磁式电流互感器暴露出铁芯易饱和等一系列严重的缺点而不能满足电力系统的要求。电子式电流互感器（ECT）以其体积小、精度高、绝缘性能好、动态范围宽等优点脱颖而出，有逐步取代传统电磁式电流互感器的趋势[2-4]。然而电子式互感器相位误差产生的原因与电磁型互感器有较大差别，同时作为继电保护设备的信号来源，对谐波测量的精度也有特定要求。本文基于Rogowski线圈电子式电流互感器的设计，分析电子式电流互感器相位误差的产生原因并研究补偿方案。

1 Rogowski线圈电子式电流互感器工作原理

电流互感器从原理上可归纳为有源型和无源型两类，目前有源型技术成熟，长期稳定性很好。本文研究数字输出的有源电流互感器，原理结构如图1所示。

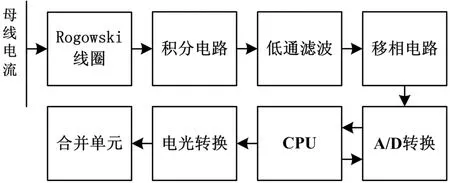
图1 电子式电流互感器结构框图

2 传感头的相差分析

Rogowski线圈是在非磁性骨架上均匀密绕导线后，再在线圈两端接上取样电阻构成的[5]。罗氏线圈是根据一次电流变化时所产生的磁通势大小来反映被测电流值的测量装置，它的测量原理主要基于安培环路定理和电磁感应定律[6]。考虑理想的线圈模型，当载流导线从线圈中心穿过，可得出闭合线圈感应电势e(t)与测量电流i(t)之间的对应关系为：

式（1）中，M为线圈回路与一次导线回路之间的互感器系数。若考虑线圈分布参数，则等效电路如图2所示，其中i2(t)为线圈中流过的一次电流，R0为线圈等效电阻，L0为线圈等效自感，C0为线圈等效杂散电容，Ra为取样电阻，Uo(t)为取样电阻端电压。

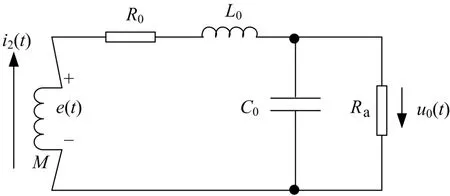
图2 Rogowski线圈等效电路

根据实际样机取样电阻Ra接近无穷大，并由等效电路推导可得线圈的输出电压uo(t)为：

由上式可知，若考虑线圈的分布参数，输出电压与一次电流之间有一定的相位差，而且此相位差会造成线圈的输出电压与一次电流不再是严格的微分关系[7]，由式（2）可知，线圈带来的相位差θ1为：

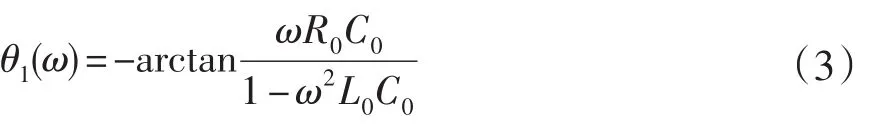
式（3）中ω为角频率。从式（3）可知，线圈本身会引入一个延迟的相位误差。根据样机线圈测得参数为L0＝0.244 mH，R0＝20 Ω，C0＝1.4 μF ，在工频下与理想微分的90°相移对比产生的相位差为-0.504°，当频率为1000 Hz时，相位差为-10.1°。同时，线圈的相频特性如图3所示：

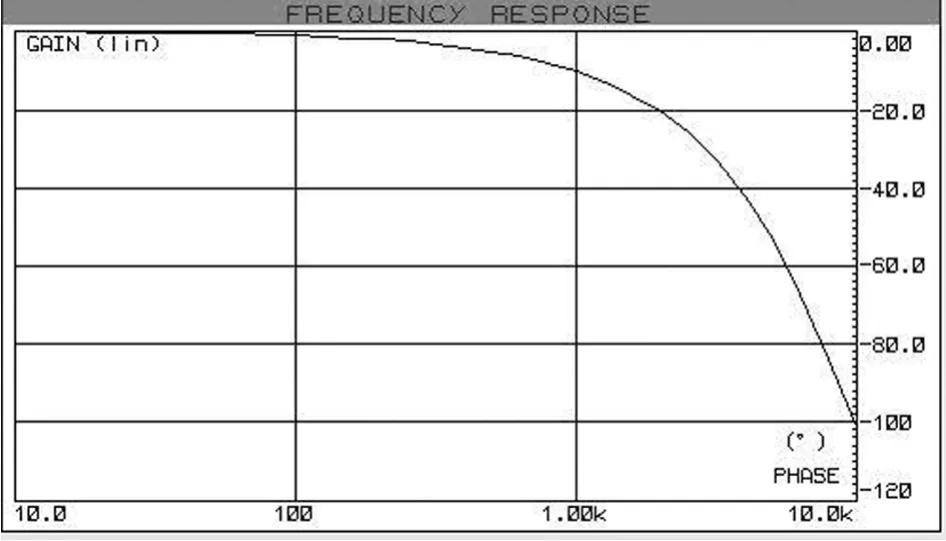
图3 空心线圈相频特性

可见线圈自身的相位差会随着频率的增大而增大，这对谐波信号的测量有重要影响，这是电流互感器相差产生的原因之一。

3 积分电路相差分析

为了使电流互感器能正确反应一次电流，并从式(1)可知，在处理电路中需加入积分电路[8]。本设计采用的是有源惯性环节积分器，后面带有一级反相电路，其电路图如图4所示。

图4 后接反相器的积分电路

其中RF为反馈电阻。设定R3＝R4，则其传递函数为：

相频特性表达式为：

当反馈电阻RF取值很大时，负反馈积分器可近似为理想积分器。样机有RF＝100 MΩ、C1＝0.47μF，在工频下与理想积分电路-90°的相移比较，此积分电路的相差θ2为+0.0039°。并可得到积分电路的相频特性如图5所示，可见积分电路的相差几乎可忽略不计。

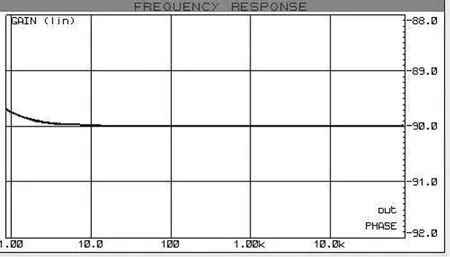
图5 积分电路相频特性

4 低通滤波器相差分析

由传感头感应出的电压信号，在传输过程不可避免地会受到高频噪声干扰信号的影响。因此，为了滤除噪声的影响，需要在信号处理过程中加入滤波环节[9]。本设计采用二阶巴特沃斯低通滤波器来完成，其电路如图6所示。

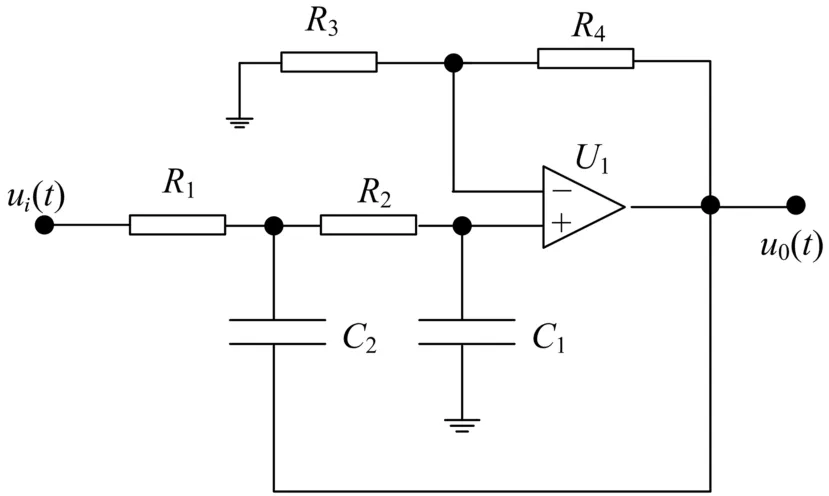
图6 低通滤波电路

设R1＝R2＝R，C1＝C2＝C，其传递函数为：

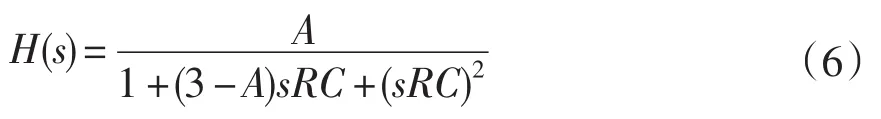
式（6）中A＝1+R3/R4，为滤波器增益。令s＝jω，推导得到相位差为：

根据样机设计有R1＝R2＝5 kΩ，C1＝C2＝0.02 μF，R3＝R4＝10 kΩ，由式（7）得在工频50Hz下滤波器引入相差θ3＝-1.8012°，当频率为1000 Hz时，滤波器引入的相位差θ3＝-46.073°。分析其相频特性，如图7所示：

滤波器引入的相位差随着频率的增大而增大，这对谐波信号的测量有重要影响，这也是电流互感器相差产生的原因之一。

5 移相电路设计

由以上分析可知，Rogowski线圈以及低通滤波器是电流互感器相位差产生的主要原因，而电子式电流互感器标准IEC60044-8对相差有具体的要求，这就要求对相位进行补偿校正，以达到标准要求[10]。根据以上分析，线圈和低通滤波器整体的相频特性如图8所示。

针对这个相位差频率特性，本文在设计过程中尝试了两种补偿方案，并进行了性能分析对比。

图7 低通滤波器相频特性

5.1 相差补偿方案一

方案一采用的电路结构，如图9所示。

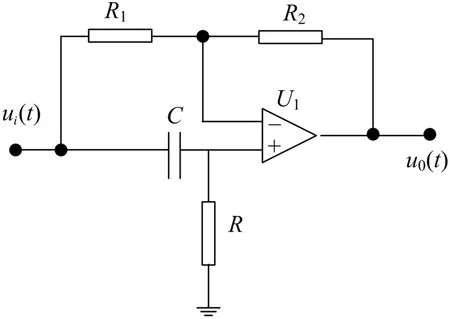
图9 全通相位超前电路

这是一个全通滤波器，设R1＝R2，推导得其传递函数为：

令s＝jω，推导得到幅频特性与相频特性分别为：

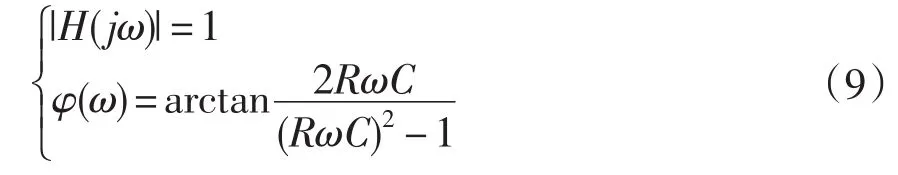
从幅频特性可知，此电路结构具有全通特性。按设计有C＝0.1 μF，R＝1.58 MΩ，相频特性如图10所示。

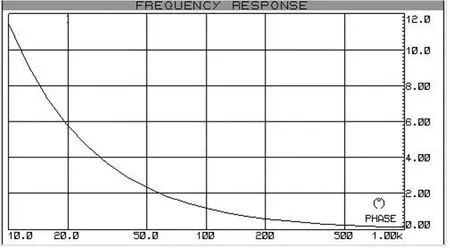
图10 全通相位超前电路相频特性

工频下的相移为+2.3083°，可补偿前面讨论的线圈和处理电路的滞后相位。但是结合前述的线圈和低通滤波整体的相频特性可知，此移相电路对于不同频率的信号不能准确补偿相位差，而电子式电流互感器标准中对谐波的测量也有具体要求[11]，故仍然不能作为很好的补偿电路，理想的补偿环节应该具有恒时延的特性。

5.2 相差补偿方案二

从相差补偿方案一分析得，要正确补偿相差，补偿环节应具有恒延时的特性。考虑到硬件电路难以实现，本文从软件移相算法进行设计。

分析t时刻电流可表示为：

则超前σ角度的电流可表示为：

以向量表示它们分别为I、Iσ，同时令：

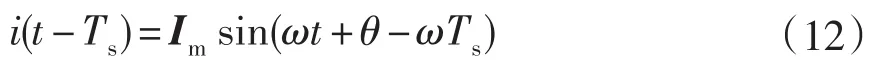
以向量表示时为I＜(-ωTs)，I＜(-2π/N)，其中N为每工频周期采样点数，可作出向量图如图11所示。

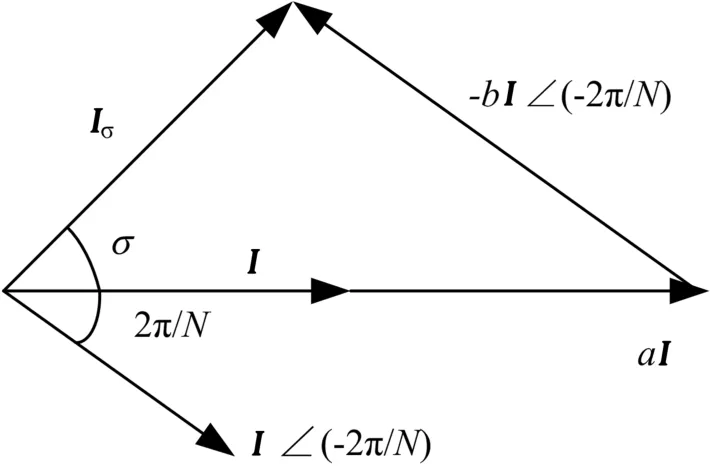
图11 超前移相向量图

设 Iσ＝aI-bI＜(-2π/N)，其中 a、b为系数，则在图11中由Iσ、aI、bI＜(-2π/N)组成的三角形中，由正弦定理可得到：

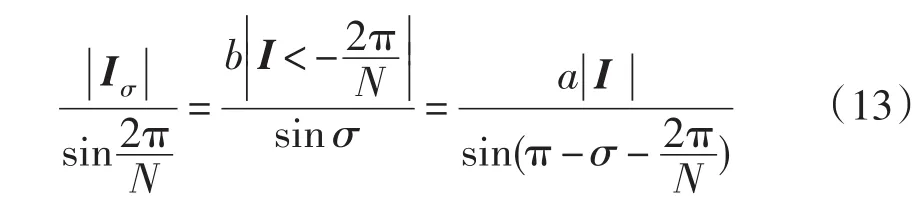
因为Iσ由I旋转得到，所以两者幅度相等，得到系数a、b为：

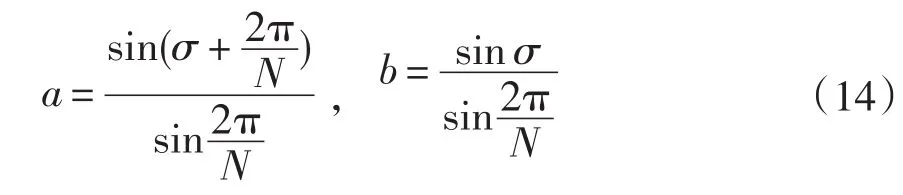
根据前述线圈和滤波器的相位差分析，需要补偿的相位可预先估计，在采样频率一定的情况下，可离线计算书系数a、b，iσ(t)即可以改写为：

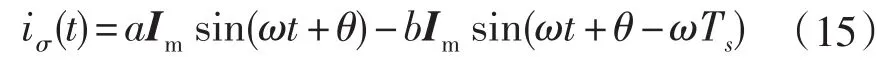
于是转为采样值计算可得到算式：

由式（16）可通过相邻两个i(t)的采样值获得超前i(t)相位σ的电流采样值，实现超前运算。

本文设计采用高速FPGA，移相运算延时极小，可不计其引起的相位误差。通过代入实际需要的移相角度，可实现准确移相。

最后对设计整机进行测试，通过小电流多次穿过线圈来等效大电流，电流输出设备用计算机继电保护控制测试仪产生，可调节电流信号频率。设定等效电流200 A，调节电流频率从48～1000 Hz，相差结果如表1所示。

由表1可知，在48～1000 Hz范围内，相差变化很小，在标准要求之内，说明移相算法对工频和其他谐波信号仍有较好的补偿作用。

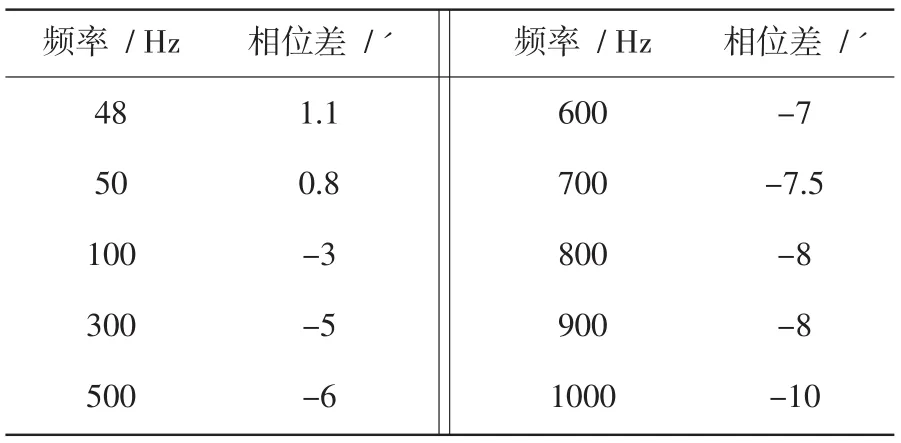
表1 相差试验结果

6 结论

通过对电子式电流互感器传感头和处理电路的分析，明确了其相差产生的原因，并对相位差提出了较为有效的补偿方法。经过推算、仿真和试验测试，结果表明了该方法的有效性，对谐波的测量精度也满足标准要求。

［1］罗苏南，田朝勃，赵希才.空心线圈电流互感器性能分析［J］.中国电机工程学报，2004，24（3）：108-113.

［2］高广玲.电子式电流互感器传变特性及适应性保护原理研究［D］.济南：山东大学，2006.

［3］张冈，王程远，陈幼平.PCB空心线圈电流传感器的暂态特性［J］.电工技术学报，2010，25（11）：85-89.

［4］王程远.PCB空心线圈电子式电流互感器的理论建模及设计实现［D］.武汉：华中科技大学，2008.

［5］周均德.电子式电流互感器Rogowski线圈传感头的研究与设计［D］.长沙：湖南大学，2006.

［6］刘延冰，李红斌，等.电子式电流互感器原理、技术及应用［M］.北京：科学出版社，2009.

［7］李维波.基于Rogowski线圈的大电流测量传感理论研究与实践［D］.武汉：华中科技大学，2005.

［8］张可畏，王宁，段雄英，等.用于电子式电流互感器的数字积分器［J］.中国电机工程学报，2004，24（12）：104-107.

［9］李维波，毛承雄，陆继明，等.分布电容对Rogowski线圈动态特性影响研究［J］.电工技术学报，2004，19（6）：12-17.

［10］Q.Chen， H.B.Li， M.M Zhang， et al.Design and Characteristics of Two Rogowski Coils Based on Printed Circuit Board ［J］.IEEE Transaction on Instrumentation and Measurement，2006，55（3）：939-943.

［11］GB/T 20840.8-2007.互感器——第8部分：电子式电流互感器［S］.