融合混沌和捕食搜索的混合粒子群算法

王 涛，刘冬华

(暨南大学信息科学技术学院，广州510632)

粒子群优化算法(简称PSO)是由Kennedy J和Eberhart R·C于1995年提出的一种优化算法[1]，粒子群算法源于对鸟群和鱼群群体运动行为的研究.粒子群优化算法由于其算法的简单，易于实现，参数少，收敛速度快，所以发展十分迅速，且在其他领域得到很好的应用.与其他智能算法类似，粒子群算法也存在易陷入早熟收敛和局部寻优能力差等缺点.目前解决这些问题的主要方法是增加种群的多样性以及和其他算法融合等[2－4].文献[5]引用了捕食搜索策略，巧妙地平衡局域搜索和全局搜索的矛盾，利用较少的粒子数解决高维规划问题，搜索速度较快且能避免陷入局部最优.

本文提出了一种用复制函数优化的融合混沌与捕食搜索的混合粒子群算法(简称CPSPSO)，该算法首先利用混沌的遍历性产生初始种群，以克服种群初始化的盲目性和随机性;其次结合了捕食搜索策略通过限制的调节，控制粒子群搜索空间的增大和减小，从而平衡搜索能力和开发能力.测试结果表明，CPSPSO用于复制多峰函数优化时表现出良好的全局寻优能力，可提高优化计算效率.

1 标准粒子群算法

设一个由m个无重量和体积的粒子组成的群体在n维搜索空间中以一定的速度飞行.第i个粒子的位置表示为:

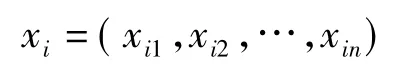
第i个粒子的速度表示为:

vi=(vi1，vi2，…，vin)

第i个粒子经历过的历史最优点表示为:

pi=(pi1，pi2，…，pin)

群体内(或邻域内)所有粒子经历过的最优点表示为:

pbest=(pbest，1，pbest，2，…，pbest，n)

则粒子的位置和速度根据以下的方程进行变化:

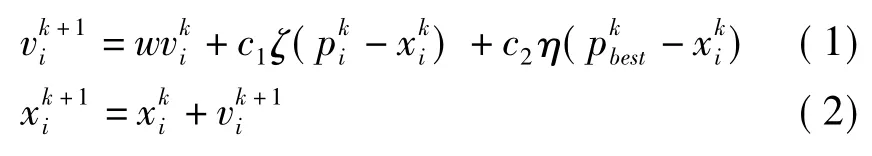
其中:c1和c2为学习因子，一般为正常数.ζ，η∈U[0，1]，是在[0，1]区间内的均匀分布的伪随机数.w为惯性权重，一般取在0和1之间.

2 捕食策略的基本原理

捕食搜索(PS)算法是由巴西学者Alexandre Linhares[6－7]在 1988 年提出的一种用于解决组合优化问题的模拟动物捕食行为的搜索策略.捕食搜索策略基本思想:在没有发现猎物和猎物的迹象时在整个捕食空间沿着一定的方向以很快的速度寻找猎物;一旦发现猎物或者发现有猎物的迹象，它们就立即改变自己的运动方式，减速速度，不停地巡回，在发现猎物或者有猎物迹象的附近区域进行集中地区域搜索，持续不断地接近猎物.在搜寻一段时间没有找到猎物后，捕食动物将放弃这种集中地区域，而继续在整个捕食空间寻找猎物[8].

3 混合算法的描述及数值实验

3.1 混沌分散的群体初始化

标准粒子群算法的初始值是随机产生的，容易陷入早熟，我们利用混沌的遍历性进行搜索跳出局部最优，将会有助于求解效率的提高与解得质量的改善.比较有名的混沌模型是一维Logistic映射，其迭代公式为

其中:k为迭代次数;μ为控制系统混沌行为的的参数，当 μ 值确定后，又任意初始值 x0∈[0，1]，可迭代出一个确定的时间序列 x1，x2，…，xk.已经证明，当μ=4时，系统没有稳定解，是[0，1]区间的满映射，式(3)完全处于混沌状态.

3.2 基于捕食策略的粒子群算法的基本思想

粒子群算法有着收敛速度快、全局寻优能力强、计算简单和鲁棒性好等优点，但其缺点是易陷入局部极优，搜索精度不高.为避免陷入局部最优，并且实现局部搜索与全局搜索的平衡，将捕食搜索策略引入到标准的粒子群算法当中.

为了把捕食搜索策略引入标准粒子群算法，本文将限制定义为每个粒子在解空间中的搜索速度，并在解空间中设置级限制，则在限制L上速度为v=vL/Numlevel.在最小限制L上初始化粒子群，使用标准粒子群算法更新式(1)与(2)搜索，试图找到较优解.若在Cthreshold次内不能找到较优解，则在限制L+1上混沌初始化，再次用式(1)与(2)进行搜索.若找到更好解，则替代较优解，并且重新计算限制，重复.通过限制级别调节，从而平衡探索能力与开发能力.其中:Numlevel为总限制级别，Cthreshold为增大限制等级的阈值，Lthreshold为放弃局部搜索的阈值，L为限制等级.

3.3 算法流程

步骤1:初始化粒子群中的粒子的位置和速度，对粒子位置用式(3)和式(4)混沌初始化，随机选择初始解 gbest，c=0，L=0;

步骤2:根据式(1)，(2)更新粒子的位置和速度，迭代n次，得到一个历史最优解;

步骤3:如果 p ＜ gbest，gbest=p，转步骤 2;否则，c=c+1，转步骤 4;

步骤4:如果c＜cthreshold，转步骤2;否则，L=L+1，转步骤5;

步骤5:如果L＜Lthreshold，初始化粒子种群，转步骤2;否则L=Numlevel－L，转步骤2.

3.4 数值仿真实验

3.4.1 测试函数

为了测试CPSPSO的性能，使用了3个常用Benchmarks多变量测试函数(表1)来进行试验，并且将实验结果与标准粒子群算法(PSO)，一般混沌粒子群算法(CPSO)的测试结果进行比较

表1 常用Benchmarks多变量测试函数

3.4.2 参数设置

在CPSPSO中，由于全局搜索能力和局部搜索能力的平衡主要是靠限制L来实现的，而学习因子和惯性权重作用于内循环当中，对全局搜索能力和局部搜索能力并没有太大的影响，所以，本文采用了固定学习因子和惯性权重，即c1=c2=2，ω=0.9－0.5t/incircul.另外，根据反复试验，本文同时调整以下3个参数，可以取得最优解:

Numlevel=粒子维数+1=9

Cthreshold=粒子维数=8

Lthreshold=2

incircul(内循环次数)=400 outcircul(外循环次数)=50

在作为对比的标准粒子群算法中，本文采用了时变惯性权重ω=0.9－0.5t/tmax，和异变学习因子c1=2t/tmax+0.5，c2= －2t/tmax+2.

在PSO 与CPSO 中 c1+c2=2.0，ω =0.8最大迭代次数为2 000.

CPSPSO，CPSO，PSO 种群的规模 N=100，维数是每个函数D表达中n的值.

3.4.3 实验结果及分析

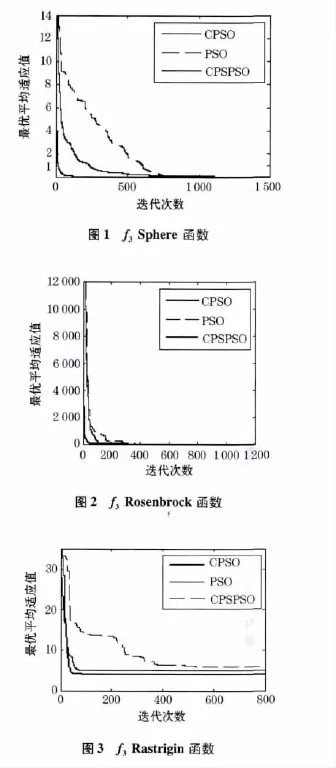
函数测试数据是利用Matlab编程实现，每个算法运行30次，取其平均值，实验结果如下表2所示.以上述3个Benchmarks函数为测试函数，最大迭代次数为2 000，每个算法运行30次，计算最优解平均值，实验结果如表3所示.图1～3是上述3个Benchmarks函数运行30次后求得的平均最优解的收敛曲线图.从表2、3中可以看出CPSPSO不仅优于PSO而且优于CPSO.

表2 迭代次数结果比较

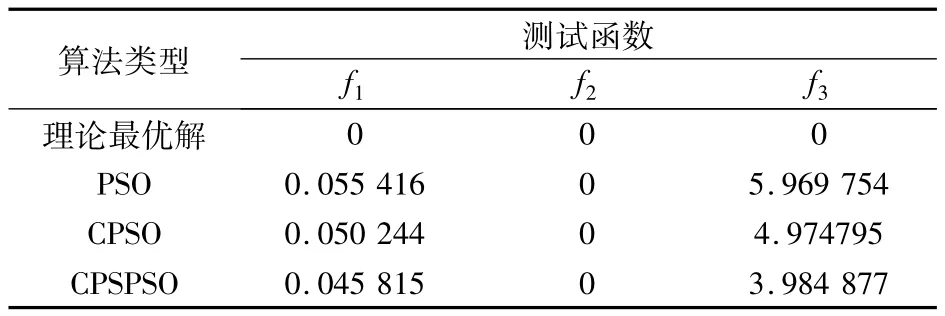
表3 最优结果比较

4 结语

本文提出了一种用于复杂函数优化的融合混沌和捕食搜索的混合粒子群算法.该算法利用混沌的遍历性初始种群，以克服种群初始化时的随机性.在搜索过程中运用了捕食策略，通过限制的调节，控制粒子群搜索空间的增大和减小，从而平衡搜索能力和开发能力.克服了标准粒子群易陷入局部最优的缺点.算法测试结果表明，CPSPSO具有较好的优化搜索性能，可提高计算的效率，在高维复杂函数优化方面有一定的实用价值.

[1] KENNEDY J，EBERHART R C.Partial Swarm Optimization[C]//Proc.IEEE International Conference on Neural Networks，Piscataway，NJ:IEEE Service Center，1995，1942 －1948.

[2] 刘瑞芳，王希云.一种混沌权重的简化粒子群算法[J].计算机工程与应用，2011，47(21):58 －60.

[3] 贾松卫，高岳林.融合模拟退火和混沌的混合粒子群算法[J].计算机工程与应用，2009，45(7):52 －55.

[4] 曾宇容，王 林，富庆亮.基于DE和PSO的混合智能算法及其在模糊EOQ模型中的应用[J].计算机应用研究，2012，29(2):438－441.

[5] 符 杨，孟令合，罗萍萍，等.索策略的粒子群算法在输电网络扩展规划中的应用[J].电力建设，2009，30(3):1－4.

[6] 乔 烨.基于捕食搜索策略粒子群算法的车辆路径问题研究[D].西安:长安大学，2008.

[7] LINHARES A.Preying on optima:A predatory search strategy for combinatorial problems[C]//Proc.IEEE Int.Conf.Systems，Man and Cybernetics，Piscataway NJ:IEEE Service Center，1998:2974 －2978.

[8] 徐耀群，王长举.一种万有引力优化算法及其收敛性分析[J].哈尔滨商业大学学报:自然科学版，2013，29(1):63－67.