基于FFT分形滤波的地球化学异常信息提取

熊 超，葛良全，王 卓，谷 懿，罗耀耀，刘 端

(成都理工大学，四川成都 610059)

0 前言

选择适当方法从表面杂乱随机的地球化学数据中提取异常信息是地球化学数据处理的核心任务。傅里叶变换作为信号处理的重要方法被广泛应用于地球物理领域，而地球化学领域的研究却相对较少，其主要原因是磁、电和地震等地球物理数据的连续性好于地球化学数据。实际上，地球化学数据虽然从表面上跳跃性很大，似乎完全是随机的，但长期地质统计学的研究表明，可以反映地球化学数据性质的区域化变量包含着结构性与随机性，只不过随机性往往掩盖了结构性。以往研究中傅里叶滤波的截止频率往往通过观察频谱或功率谱确定，由于地球化学数据本身跳跃性大，功率谱特征并不明显，且观察结果容易受到人为因素影响。为解决这一问题，本文使用多重分形方法解析傅里叶变换后的功率谱，以确定区域背景和局域背景的截止频率，并使用此频率对原始数据做低通滤波提取地球化学异常信息。

1 快速傅里叶变换(FFT)原理

对于数组X［n］，可利用傅里叶级数展开表示为:

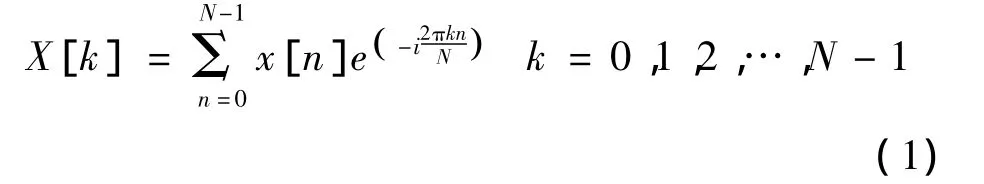
这一将信号从时域表示变换到频域表示的过程叫做离散傅里叶变换(DFT)。将这一方法迁移至地球化学领域，地球化学数据可以认为是由这些不同强度和频率的频谱成分排列叠加而成，X［n］为测点元素含量值，其反变换为:

式(1)中可知，若要计算一组地球化学数据(即整个频谱中N个离散傅里叶变换)，需要做N2次复数乘法和N(N－1)次复数加法，而面对N动辄几千多达几十万的海量地球化学数据时，计算量将迅速增长。为避免冗余计算，下面采用基于Danielson-Lanczos引理的FFT算法，即如果数据点N的总数是2的整数幂，此时的DFT可以重新记作两个DFT的和:

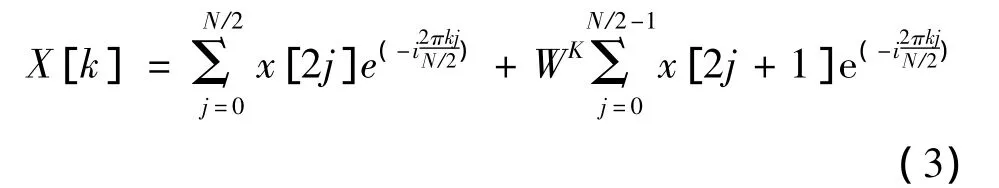
2 多重分形方法

分形理论是研究自然界和社会活动中广泛存在的无序而具有内部自相似性的系统的理论，近年来一些专家学者注意到地质学中的自相似现象，并将分形理论引入地球科学之中，这种自相似性有助于分解不同的地质过程与地质体，提取出确定性、规律性的参量，揭示复杂事物中新的深刻而定量的规律，它从新的角度研究元素分布与富集的意义。地球化学景观的形成经历了复杂地质历史的演化，元素曾发生过不同尺度的迁移和富集，如果把地球化学景观的整个地质地球化学作用过程视为随机过程，刻画这过程的不同尺度的地质地球化学作用是等概率发生的，那么地球化学景观可能具有自相似特征。

分形模型:

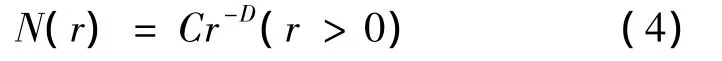
式(1)中，r为特征尺度;C＞0为比例常数，D＞0为一般分维数;N(r)=N(≥r)为尺度大于等于r的和数。

设地球化学元素做FFT变换后某一含量的频率为{fi}，i=1，2，…，N，记:

(5)代入(4)，两边分别取对数，得到一元线性回归模型:

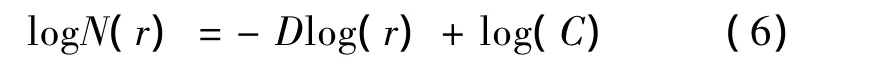
用最小二乘法求出斜率D的估计量，即为分维数;其散点大致分布在几段直线上，采用分段拟合分别求出线性方程。

3 方法实验

此次选取新疆西天山某测区1∶50000土壤X荧光化探样品中Sr元素局部测量数据为例，试图采用上述方法提取异常信息，并与传统异常计算方法做比较。元素含量测试由成都理工大学自主研发的IED-2000P手提式多元素X荧光分析仪完成，元素检出限小于100μg/g，符合 DZ/T0011 －91《1∶50000地球化学普查规范》中的检出限要求。测量时间设定为500s。图1(a)为Sr元素含量测量值。

按式(3)对Sr元素含量数据做快速傅里叶变换后的功率频谱如图2所示(注:测区样品数为432个，不足2的整数幂部分以0补齐)。从地球化学角度看，频谱图中高频部分代表数据中的噪声;低频部分代表背景;而低频的背景部分又可以根据其对应的周期大小分为区域背景和局域背景(即异常下限)，并可继续细分。图2中仅凭观察无法确定高低频率间的界限，而以往研究中大都根据经验区分高频与低频，存在较大的主观因素和盲目性，为克服这一缺陷，这里采用多重分形方法确定滤波的截止频率。

图1 Sr元素元素含量图Fig.1 Sr content chart

图2 Sr元素功率频谱图Fig.2 Sr Power spectrum chart

具体步骤为:(1)按一定间隔设置Sr元素频率尺度r，求出大于r的所有样本频率之和N(r);(2)将［f，N(r)］数据集取对数后制作散点图;(3)将图中数据分为三段，利用剩余平方和最小原则进行最小二乘拟合，拟合直线的交点f1、f2即为区域背景和局域背景的截止频率。拟合结果如图3。

图3 Sr元素功率谱分形拟合图Fig.3 Sr fractal fitting chart of power spectrum

拟合方程如下:

联立(7)、(8)、(9)解得:

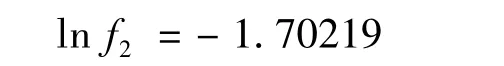
将ln f1、ln f2求真数得:

使用f1、f2作为截止频率分别对原始数据做低通滤波变换，结果如图1(b)、1(c)。从图1(b)中可看出，测区内元素分布呈现东西部高于中部的趋势，这一现象与测区自东向西跨越含钙质砂岩、浆屑凝灰岩等不同岩性的地质背景相吻合，说明傅里叶低通滤波不仅能去除地球化学数据的噪声，还能起到还原地球化学场结构的作用。而图1(c)对比1(a)可知原始数据中高频率噪声已基本被剔除，这一过程与传统异常下限计算过程中迭代剔除特高值的过程颇为相似，滤波后得到的结果即为各点的异常下限值。以下使用不同方法对经f1、f2快速傅里叶滤波后的数据进行异常提取，并与传统统计方法做比较。

(1)传统统计方法

传统统计方法是假设测区数据服从正态或对数正态分布，当测量数据不符合正态分布时，要对原始数据进行极异常点(特高值、特低值)做连续迭代处理，一般采用平均值(X)±3×均方差(S)为上下限迭代剔除，直至无离群点数值可剔除为止，即所有数据全部分布在X－3S与X+3S之间，即形成背景数据，再以背景值加2倍均方差(X+2S)计算异常下限并成图如4(a)。

(2)区域背景异常提取

经f1滤波后的数据可以看作是结合地球化学场结构的“动态”背景值，此时对滤波后的数据求平均值(X')和均方差(S')，并类似于(1)中(X'+2S')计算“动态”异常下限成图如4(b)。

图4 (a)传统统计方法、(b)区域背景异常、(c)局域背景异常Fig.4 (a)Traditional statistics method;(b)anomalies of regional background;(c)anomalies of local background

(3)局域背景异常提取

f2低通滤波后的数据作为测区的局域背景值，即异常下限值，与(2)中相似，每点的异常下限各不相同，但这里的异常下限不需要再经过任何处理，直接成图后结果如4(c)。

4 结果与讨论

三种方法中，传统统计方法所圈定的异常范围最大，原因是此方法前期对原始数据进行了迭代剔除，确定的异常下限值并非由全部数据，而只是由背景数据决定，此方法只对度量一般值效果较好，且同一测区不同岩性上采集的样品数据均使用相同的异常下限，忽略了地球化学场对元素分布的控制，地质背景差异的趋势由于取平均值而弱化，故在高背景值区域容易呈现假异常，而同时低背景值区会忽略弱异常;由区域背景提取的异常由于背景值是动态的，已将不同地质背景导致的差异包含于数据中，所以对比图4(a)，4(b)在测区东部高背景值区的条带状异常面积有减少，而中部和底部异常区域内也出现了多个浓集中心，说明传统方法在低背景区域漏掉的弱异常已被成功提取出来;局域背景提取异常有别于前两种方法之处在于不需要对滤波后的数据进行任何的额外处理便可直接使用，异常下限值仅由原始数据质量本身决定，此方法可以在完整保留原始数据信息的前提下圈定异常，图4(c)中测区东部的异常由于高背景的压制几乎消失，且前述中部和底部两处异常浓集趋势与范围均有明显降低，由此看出局域背景提取异常法对地球化学异常的敏感度不及前两种方法，建议在进一步异常查证过程中采用此方法以增加查证的精确性。

Changjiang Li，Tuhua Ma，Xingsheng Zhu，Guowu Wang.2002.Principle of mineral deposit size forecasting implication for gold resource potential evaluation in China［J］.Acta Geoscientia Sinica(English E-dition)，76(3):378

Cheng Qiu-ming.2001.Spatial self-similarity and geophysical and geochemical anomaly decomposition［J］.Chinese Journal Geophysics，16(2):8－17(in Chinese with English abstract)

Cheng Q，Agterberg F P，Ballantyne S B.1994.The separation of geochemical anomalies from back ground by fractal methods［J］.Journal of Geochemical Exploration，51:109

Dai Hui-min，Gong Chuan-dong，Bao Qing-zhong，Sun Zhong-ren，You Hong-liang，Jin Xin，Gao Fei.2010.A comparison of several threshold determination methods in geochemical data processing:A case study of stream sediments in chabaqi area of innermongolia［J］.Geophysical and geochemical exploration，34(6):782 －786(in Chinese with English abstract)

Ding Shi-jiang，Zhai Yu-sheng，Deng Jun.1998.Fractal Analysis of gold deposit distribution in China［J］.Geological Review，44(2):188(in Chinese with English abstract)

Hou Gui-ting.1998.Fractal simulation and classification of folds［J］.Acta Geoscientia Sinica(English Edition)，72(2):217

Journel A G，Huijbregts C.1978.Mining geostatistics［M］.Academic Press:1－303

Mark Owen.2008.Practical signal Processing，1stedition［M］.Cambridge University Press:1－228

Ouyang Li-sheng.2010.Application of fractal filtering in unusual decomposition of geophysical data［J］.South china journal of seismology，30(4):70－75(in Chinese with English abstract)

Pei Tao，Bao Zheng-yu.1999.The experiment of fourier transform to the geochemical data processing［J］.Journal of Changchun University of Science and Technology，1(1):88 －92(in Chinese with English abstract)

Shen Wei.2002.Chaos fractal and mineral prediction［M］.Beijing:Geological Publishing House:8－18(in Chinese with English abstract)

Shen Wei，Sun Fang-yong.2003.Fractal distribution and its application to large-sized mineral deposits［J］.Acta Geoscientia Sinica，24(supp):263(in Chinese with English abstract)

Shi Jun-fa.2000.Fractal distribution of the reserves of gold deposits in Jiaodong and its geological implication［J］.Geological Review，46(Supp):293(in Chinese with English abstract)

Zhou Jian-ping.2007.Practical course of Origin(7.5 Edition)［M］.Xi'an:Xi'an Jiaotong University Press:223－227(in Chinese with English abstract)

Zhang Zhe-ru，Mao Hua-hai.2000.Fractal theory and Ore-forming［J］.Earth Science Frontiers(China University of Geosciences，Beijing)，7(1):195－204(in Chinese with English abstract)

［附中文参考文献］

成秋明.2001.空间自相似性与地球物理和地球化学场的分解方法［J］.地球物理学进展，16(2):8 －17

戴慧敏，宫传东，鲍庆中，孙中任，尤宏亮，金鑫，高飞.2010.区域化探数据处理中几种异常下限确定方法的对比－以内蒙古查巴奇地区水系沉积物为例［J］.物探与化探，34(6):782－786

丁式江，翟裕生，邓军.1998.中国金矿床分布的分形研究［J］.地质论评，44(2):188

欧阳立胜.2010.分形滤波(S-A)技术在物探数据异常分解中的应用［J］.华南地震，30(4):70－75

裴韬，鲍征宇.1999.傅立叶变换在地球化学数据处理中的应用［J］.长春科技大学学报，1:88－92

申维.2002.分形混沌与矿产预测［M］.北京:地质出版社:8－18

申维，孙方勇.2003.分形分布函数及其在大型矿床中的应用［J］.地球学报，24(增刊):263

施俊法.2000.胶东金矿床的储量分形分布及地质意义［J］.地质论评，46(增刊):293

张哲儒，毛华海.2000.分形理论与成矿作用［J］.地学前缘(中国地质大学，北京)，7(1):195－204

周剑平.2007.Origin实用教程(7.5版)［M］.西安:西安交通大学出版社:223－227