模糊识别模型解决水资源承载能力综合评价问题分析

李庆林

(江西省石城水文站，江西 赣州 342700)

水资源的承载力是指在某个特定的时间内预见区域内水资源的可开发的潜力。研究承载能力主要是在可持续开发的目标下维持如何在承载范围内进行持续开发，并保证合理利用，以此保证水资源的利用效率。目前对水资源的承载力的研究与综合性评价主要依靠的是模糊判断法、多目标决策区间法、投影寻踪法、主要成分分析法等等。不同的方法尤其特有的价值，其中模糊识别模型的方式作为模糊评判法的重要技术措施，可以在复杂的资源条件中对水资源的承载力进行综合性的评价，是一种较为普遍的水资源研究方式，下面就对称进行简要的介绍。

1 模糊识别模型下的水资源承载能力综合评价

1.1 承载能力的指标体系与标准确立

针对现有的研究成果，针对复杂的研究对象往往进行因素分层，利用单元选择大量的指标构建一个庞大的评价体系。而在实际的操作中容易形成瓶颈，即某些数据不易获取。所以在研究城市水资源承载力的综合评价时，进行了影响因素的总体划分，一方面水资源的开发与利用是社会发展的重要保障，提高水利资源的承载的状态作用，利用水资源的支撑系数描述;一方面经济发展对水资源的承载能力起到的压力效果，是降低水资源承载能力的副作用，利用水资源的压力系数表达。而水资源的承载能力的状态则是二者综合评价后的客观反应。所以在建立水资源评价体系的时候必须建立一个水资源承载能力的评价指标体系，然后按照这个指标进行综合性评价，这样既可考虑到全方位的影响因素，以反映各个方面的指标。

在模糊识别的思路下，分级条件下面最大的隶属度原则是不适用性，对于水利资源的承载能力的状态系数、支撑系数、压力系数而言综合评价的特征系数越小则模型越优化。在分析中借助正向与逆向来划分指标类型，这样可以保证评价的相对准确。对于正向系数而言，指标越大则水资源的承载力也大，对于水资源的承载压力则小，如平均水资源占有量、第三产业附加值比重等等。而逆向指标则是越大其对水资源的支撑力弱，对水资源的压力也就愈大，其承载能力状态也就高，如GDP用水比例、生态环境用水量等等。综合上述分析，可以从代表性指标入手，选择可获得性与可比性，从定性与定量的层面来对指标进行单体检验与整体检验，由此提出一些非重要指标，进而形成一个综合性的指标表。如1、2表。

水资源支撑力的系数标准的确定是参考现有的研究成果分级，结合全国水资源和社会经济发展的趋势进行了整合与调试。以万元GDP用水量的指标作为分级标准。按照我国近期公布的水资源公报数据进行参考，从全国的整体情况看，万元GDP用水量看，大于1000m3的只有两个省份，小于200m3的有13个省份和市区，其中北京、天津较低，呈现这样的差异主要是因为我国的经济发展存在明显的地区性差异，国内发达城市的万元GDP用水量明显小于全国的平均水平。所以在分析该项指标的时候必须考虑全国的平均水平，所以按照中间值进行取舍，将140和60m3作为下限与上限，而将24m3作为最优的标准，将220m3作为最差标准线，以此形成一个水资源支撑指标的核心参数，以此对其他标准进行调整，形成了下表1。

表1 水资源支撑力系数指标

关于水资源的压力指标的确定，在研究成果中对我国全社会的经济发展与水利资源的利用进行了调整与整合，利用人均GDP为指标的依据，利用这个分级来联系水资源的压力指标。按照我国现有的发展趋势，以三步走为基础，将经济发展的水平以温饱、初步小康、中等小康、全面小康、初步富裕、中等富裕六个阶段。进而形成一个以GDP为标准的层次，然后将水资源的压力指标与之整合，进而形成一个压力系数的指标标准值，如表2。

表2 水资源压力系数指标

2 水资源承载能力的模糊识别

综合上面的基础数据与等级划分，就可以利用模糊识别的理论进行分析，其中建立模糊集、相对差异函数、相对比例函数等形成一个完整的模糊集理论，并将其用于水资源的承载力分析。假设水资源承载力识别的有n个样本集合如:

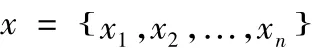
其中j个样本的特性被描述为m个值如下:

这样在集合中m×n阶就可形成一个特征指标矩阵如下:

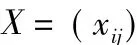
公式中xij是样本j指标i的基本特征值;i值为(1，2，3…，m);j值为(1，2，3，…，n)，按照这个样本集合中 c个级别，并对其进行辨识，则有m×c阶指标，并形成矩阵如下:

公式中yih级别h就是在j特征指标下的参考数据。

按照指标标准形成的矩阵和有待病假的典型城市的实际情况，就可形成一个水资源承载能力的可变i和，使之形成吸引域矩阵和范围域矩阵:

按照水资源承载能力的等级c来确定上面的吸引域中的相对差异度形成一个相关与Mih的矩阵:

根据上面的公式进行真理，将其特征值进行区分，利用研究文献中提出的相对差异函数定义计算向对的差异度，此时判断Mih的左右来划分，如Xij在Mih左侧，此时其相对差异函数的模型就可如下式:

当xij在Mih点右侧时，其相对差异函数模型如下式:

如果此时xij在范围之外则有公式

按照上面的分析，β是非负的指数，可以将其定义为1，即差异函数模型是线性函数。公式中的数据满足当xij=a、xij=b时，DA(xij)h=0;当 xij=Mih 时，DA(xij)h=1;如 xij=c、xij=d时，DA(xij)h=-1。符合相对差异函数定义。根据相对隶属度公式计算指标对h级的相对隶属度形成矩阵如下:

利用上述计算可以形成一个模糊评价模型:

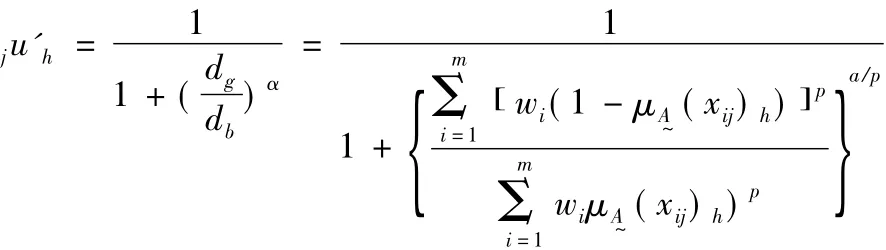
公式中利用非归一化的综合对象隶属度;优化准则参数其值为1或者2;权重度、识别指标、距离参数，这样上面的公式就可以进行转变，成为模糊识别模型。通常情况下，模型式(16)中a与p可有4种搭配:

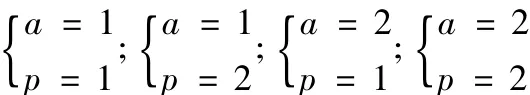
由式模糊模型可得到非归一化的综合相对隶属度矩阵:

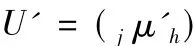
按照四种搭配，归一化处理得到综合相对隶属度矩阵:

按照模糊的概念在分级的过程中，最大的隶属度原则将被弃用，应用的级别将以下式为标准:

按照这样的样本分析与级别评价，H则可以最终确定为评价等级，如果将c确定为5，则形成下表3，说明了各个等级对应的级别变量所产生的取值范围。

表3 级别判定标准范围

3 结束语

水资源危机是当前经济发展所必须面对的问题，水资源对经济发展的制约已经十分明显，所以对水资源的承载能力的研究从来都没有停止过。上述利用的是一种可变模糊识别模型，从定量与定性两个层面对城市水资源承载力识别，利用标准系统建立，从而实现了城市水资源综合性评价。