基于遗传算法的线性二次型最优控制器设计及仿真
2013-08-16宋召青于华国
童 新 宋召青 于华国
1. 海军驻北京航天一院军事代表室,北京 100076 2. 海军航空工程学院七系,烟台 264001 3. 中国人民解放军92154部队,烟台 264001
基于遗传算法的线性二次型最优控制器设计及仿真
童 新1宋召青2于华国3
1. 海军驻北京航天一院军事代表室,北京 100076 2. 海军航空工程学院七系,烟台 264001 3. 中国人民解放军92154部队,烟台 264001

针对一类线性二次型最优控制问题,提出了一种基于遗传算法的线性二次型最优控制器设计方法,把多个不同的设计要求转换为不等式约束,并且将加权阵的选取问题表示为一个多目标优化问题,采用遗传算法优化加权阵参数,找到同时满足频域和时域性能要求的最优控制器。将该方法应用于倒立摆最优控制器设计中,结果满足给定性能要求。 关键词 最优控制;遗传算法;多目标优化;仿真
线性二次型(LQ)最优控制问题工程易于实现、使用方便,是许多方法的理论基础,很多控制问题可以作为LQ最优控制问题来处理。
在LQ最优控制器的设计中,其加权阵不易确定。目前,对于加权阵的选取,还没有系统、有效的一般方法,主要是一些定性的指导性原则,更多的是依赖于设计者的经验,这一问题已受到人们的广泛关注。文献[1]首先提出了如何通过给定极点来得到权矩阵。近年来,文献[2-4 ]在文献[1]的方向上作了相当的研究工作。但问题都仅限于通过闭环极点来确定权矩阵,并未明确提出按时、频域指标要求来选取合适的权矩阵。
LQ最优控制器的设计是先确定权矩阵、后求解控制器,使系统满足给定的性能指标要求。选择不同的加权阵,系统所能满足的时、频域性能也会不同,若将权矩阵看作变量,当权矩阵变化时,系统所能满足的时、频域性能也会变化。因此当给定系统所要满足的时、频域指标后,可以将LQ设计转化为一个优化权矩阵,使设计的闭环系统满足给定性能指标要求的多目标优化问题,而此多目标优化问题通常是一个非凸的、非光滑的及各子目标函数相互冲突的优化问题,传统的优化方法难以求解。
遗传算法是一种有效的全局优化搜索算法,特别适于处理传统寻优方法难以解决的非凸寻优问题。因此,本文采用遗传算法优化加权阵参数,搜索到同时满足给定性能要求的控制器。采用该方法设计倒立摆控制器,使得闭环系统满足给定的性能指标要求。
1 LQ最优控制
考虑如下的线性被控系统:
(1)
其中x∈Rn为状态向量,u∈Rm为输入向量,x0为t0时刻状态向量的初始值,并考虑一个二次型目标函数:
其中Q∈Rn×n和R∈Rm×m分别为给定的实对称权矩阵,且Q为正半定,R为正定。
定理1[5]设线性定常被控系统为式(1),当(A,B)完全能控且(A,C)完全能观时,二次型性能指标为式(2),其中Q,R均为正定定常矩阵,u(t)无约束,则使得J为最小的最优控制存在且唯一,可表示为:
u*(t)=-R-1BTPx*(t)=-Kx*(t)
(3)
其中,定常反馈增益阵K=R-1BTP,P是Riccati代数方程:
PA+ATP-PBR-1BTP+Q=0
(4)
的正定解。由状态反馈式(3)所构成的闭环系统:
(5)
是全局渐进稳定的。
2 小生境遗传算法
小生境遗传算法[6]是一种适用于多峰函数优化的遗传算法。该算法通过借鉴生物界中小生境这一现象,能够把群体中的各个个体分散到多个峰,从而找到更多的最优解。
一种小生境遗传算法可描述如下:
1)设置进化代数计数器t=1,随机生成M个初始个体组成初始群体P(t),并求出各个个体的适应度Fi(i=1,2,…,M);
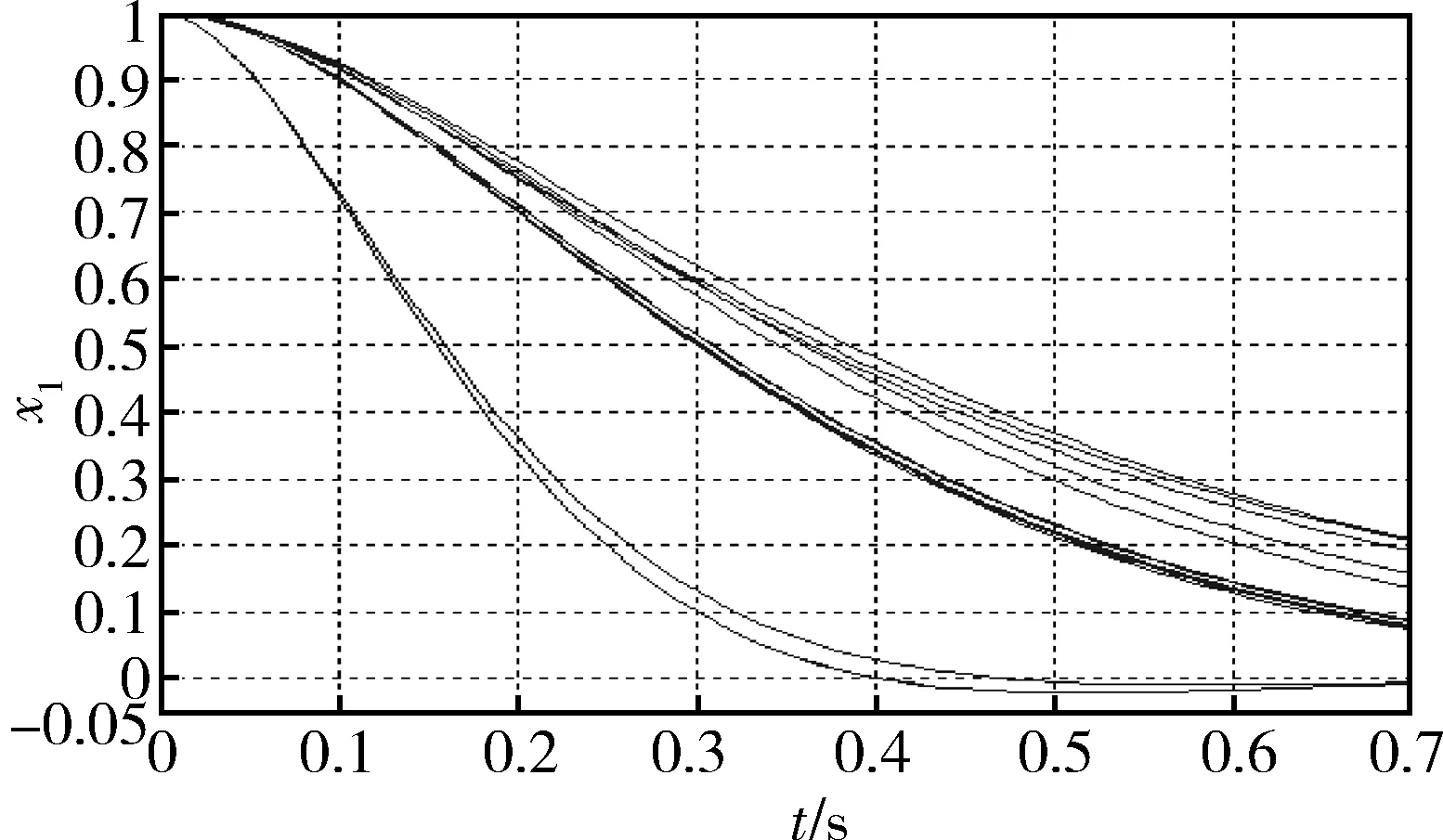
2)依据各个个体的适应度对其进行降序排序,记忆前N个个体(N 3)选择:对群体P(t)进行比例选择运算,得到P′(t); 4)交叉:对选择出的个体集合P′(t)作单点交叉运算,得到P″(t); 5)变异:对P″(t)作均匀变异运算,得到P″(t); 6)小生境淘汰:将第1)步得到的M个个体和第2)步所记忆的N个个体合并在一起,得到1个含有(M+N)个个体的新群体;对这M+N个个体,按照下式求出每2个个体X和Y之间的海明距离: (其中,i=1,2,…,M+N-1;j=i+1,…,M+N。) Fmin(Xi·Xj)=Penalty 依据这(M+N)个个体的新适应度对各个个体进行降序排序,记忆前N个个体; 7) 终止条件:若不满足终止条件,则更新进化代数计数器t=t+1,并将第6)步排序中的前M个个体作为新的下一代全体Pi(t),然后转到第3)步;若满足终止条件,输出计算结果,算法结束。 3.1 LQ控制器设计中的优化问题 LQ最优控制器的设计中,当给定系统的时、频域指标后,可以将设计转化为一个优化权矩阵,以使设计的闭环系统满足给定性能指标要求的多目标优化问题。 在多目标优化问题中,将权矩阵Q和R看成自变量,而闭环系统所需满足的性能指标可表示为一组不等式约束条件。当给定标称系统后,可按如下步骤建立多目标优化问题: 1) 确定系统所需满足的性能指标要求(包括时间响应、稳定度、鲁棒性等要求),将其转化为约束条件,即gi(Q,R)≤0,i=1,2,…,n; 2) 确定系统的子目标函数fj(Q,R),j=1,2,…,m,子目标函数可以是反映单一性能要求的函数,也可以是反映多个性能要求的函数加权和; 3) 经过步骤1)和2)后,优化问题可表示如下: s.t.(Q,R)∈Ω, Ω={(Q,R)|gi(Q,R)≤0,i=1,2,…,n} (6) 其中,gi≤0是一组反映时间响应(如上升时间、超调量、稳定时间等)和鲁棒性等要求的不等式约束;f为要求最小化的性能指标函数。 通过上述步骤建立的多目标优化问题,有时会出现Ω为空集的情况,将导致无解;而有时则会解集过大,求解速度等不能满足要求。因此为了克服这些问题,有效的方法是放松或严化不等式约束条件,此时不等式条件应改写为: gi-αiκ≤0,i=1,2,…,n (7) 这里主要是引入了αiκ项,其中κ≥0是实变量,而αi,i=1,2,…,n是可能为正、为负或为0的数值,分别对应于约束条件放松、严化或不变动的情况。通过变量κ的调整,有望得到可接受的解。 上述优化问题通常是一个非凸的、非光滑的及各子目标函数相互冲突的多目标优化问题,传统的优化方法难以求解,因此,可以采用有效的数值搜索算法—基于小生境的遗传算法来求解上述优化问题。 3.2 参数结构和编码 对于多变量系统,权矩阵一般都采用对角矩阵形式,则Q,R可用如下方式表示 Q=diag(q1,q2,...,qm) (8) R=diag(r1,r2,...,rn) (9) 其中qi∈[ki1,ki2],ki2>ki1≥0,i=1,2,…,m,ri∈[li1,li2],li2>li1≥0,i=1,2,…,n。 因此,通过上述方式确定了变量Q,R的参数结构,可将Q,R合成一个参数变量即(q1,q2,...,qm,r1,r2,...,rn),以便于遗传算法的操作。 采用二进制编码方法对上述参数进行编码,将每一个参数变量中的每一个分量转化为二进制表示,根据求解精度和分量的变化区间([ki1,ki2],[li1,li2]),确定每一个分量的二进制位数,对应分量的二进制表示如下: qi=(biki…bi1bi0),i=1,2,…,m (10) ri=(b(m+i)k(m+i)…b(m+i)1b(m+i)0),i=1,2,…,n (11) 其中,ki,(i=1,2,…,m+n)是对应的分量的二进制位数。 在遗传算法的操作中,需将上述各分量的二进制串合成为一个二进制串,构成一个染色体X: X=(b1k1…b10b2k2…b20…b(m+n)k(m+n)…b(m+n)0) (12) 通过上述方式确定算法中的个体,同时,在算法中,一旦个体给定,也可以通过相反的方式,将每一个体中对应分量的二进制串解码成相应的分量,构成权矩阵Q,R。 3.3 遗传算法运行参数 遗传算法中需要选择的运行参数主要有个体编码串长度l、群体大小M、交叉概率Pc、变异概率Pm和终止代数T等。这些参数对遗传算法的运行性能影响较大,需要认真选取。 3.4 初始群体生成 根据编码原则可知,算法中的染色体二进制串位数为k1+k2+…+km+km+1+…+km+n,则生成每一个初始个体时,个体中的每一位都在0,1之间随机选择一个数,按这样的方式随机生成M个个体。 3.5 目标函数和适应度函数 针对每一个个体X,按(Q,R)组成的参数中的分量对应于个体相应二进制的位置,提取各个分量,即 q1=(b1k1…b11b10),q2=(b2k2…b21b20),… (13) r1=(b(m+1)k(m+1)…b(m+1)1b(m+1)0)…, rn=(b(m+n)k(m+n)…b(m+n)1b(m+n)0) (14) 由此可得权矩阵Q和R。 得到Q和R后,采用基于Riccati方程的方法,求解LQ控制器K,得到闭环控制系统,计算各性能指标fi(i=1,2,…,m)和不等式约束条件gi(i=1,2,…,n)。 采用距离函数法,将多目标函数组合成一个基于需求水平向量y的目标函数: (15) 其中,y=(y1,y2,…,ym+n)。 得到了目标函数值后,按一定的转换规则将其变换为个体的适应度,并对个体适应度作尺度变换以提高遗传算法的效率。 3.6LQ控制器加权阵优化 LQ最优控制器的加权阵选取,是一个非凸的、非光滑的及各子目标函数相互冲突的多目标优化问题,采用基于小生境的遗传算法进行优化,其算法如下: 1) 给定标称对象G(s),设计不等式约束gj(j=1,...,n)、子目标函数fi(i=1,2,...,m)和需求水平向量y; 2) 确定权矩阵的参数表示方法及各分量的搜索空间([ki1,ki2],[lj1,lj2]),其中i=1,2,…,m;j=1,2,…,m; 3) 进入遗传算法搜索过程: ① 选取遗传算法的各个控制参数,如群体规模M、选择概率、交叉概率及变异概率; ② 按 3.4节中的方法产生初始群体; ③ 按 3.5节中算法给每个个体分配适应度值; ④ 依据各个个体的适应度对其进行降序排序,记忆前N个个体(N ⑤ 选择:采用同时保留最佳个体的锦标赛选择方法进行选择; ⑥ 交叉:将选择后的个体两两随机匹配,再进行交叉繁殖; ⑦ 变异:以小的概率随机改变个体的一些串位的值; ⑧ 小生境淘汰:将M个个体和步骤④中记忆的N个个体合并在一起,得到1个含有(M+N)个个体的新群体;对这(M+N)个个体,求出每2个个体X和Y之间的海明距离: (i=1,2,…,M+N-1; j=i+1,…,M+N) Fmin(Xi·Xj)=Penalty 依据这(M+N)个个体的新适应度对各个个体进行降序排序,记忆前N个个体。 ⑨针对新产生群体的每1个个体,按3.5节中算法计算目标函数值,如果满足算法终止条件(如超过给定的最大代次T),则结束算法;否则,按3.5节中算法给每个个体分配适应度值,重复3.4节。 上述算法的特点保证了在1个函数峰内只存在1个较优的个体,这样每1个函数峰就是1个小生境。通过上述算法的计算,可以得到一系列的最优解,因此在得到满意的加权阵,设计满足要求的LQ控制器的同时,也可以对这些加权阵进行选择,考虑其它方面有较好性能的权矩阵。 以倒立摆为例,倒立摆系统的模型如下[7]: (16) 其中x1表示摆与垂直线的偏角,x2表示角速度。g=9.8m/s2是重力加速度,m=2kg是摆的质量,2l=1m是摆的长度,a=1/(m+M),M=8kg是小车的质量,u是应用于小车的作用力。 在点(0,0)线性化,得到线性化模型: (17) 1) 算法中的编码和控制参数的选取 由于Q为半正定阵,R为正定阵,同时,一般在多变量系统设计中,Q和R取对角阵,因此针对倒立摆模型,取 (18) 其中q1∈[1,500000],q2∈[1,500000],r1=[1,100]。 取群体规模N=31,交叉概率pc=0.80,变异概率pm=0.001,终止代次D=71,小生境距离L=100,惩罚项Penalty=1000; 2)性能指标和目标函数 3) 遗传算法优化结果 采用3.7节中算法优化LQ控制器设计中的加权阵Q和R,得到加权阵后,采用基于Riccati方程的方法计算最优控制器。 图1显示了算法中每一代次相对应的闭环系统时间响应曲线。 图1 每代次对应的闭环系统时间响应曲线 搜索到的加权阵为: (19) 相应的最优控制器为 K=[-617.4927, -83.8396]。 4) 性能评价 最优控制器对应闭环控制系统性能指标为:系统过渡时间小于1s,超调小于1%。采用提出的方法取得了满意的设计结果,达到了给定的设计目标要求。 本文提出了一种基于遗传算法的LQ控制器设计方法,把多个不同的设计要求转换为不等式约束,并且将加权阵的选取表示为一个多目标优化问题,采用遗传算法优化加权阵参数,可以找到同时满足频域和时域性能要求的最优控制器。这种设计方法将加权阵的选取过程规范化、自动化,简单、直观,具有一定的应用价值。同时该方法不仅适用于LQ控制器设计,也能方便地应用于LQG和H2控制中的加权阵的选取。此方法应用于倒立摆控制中,得到了满足给定性能要求的控制器。 [1] Kalman R E. When is a Linear Control System Optimal?[J]. Trans. ASME(D), 1964, 86(1): 51-60. [2] Wang Yaoqing. The Determination of Weighting Matrices in LQ Optimal Control Systems[J].ACTA Automatica Sinica,1992,18(2):213-217. [3] Wang Yaoqing.An Analytical Solution to the LQ Inverse Problem for SISO System[J].Control Theory & Application,1996,13(1):115-118. [4] Wang Yaoqing.A Numerical Algorithm for the Weighting Matrix Q of LQ Optimal Control Systems[J].Control and Decision,2000,15(5):513-517. [5] 王德进.H2和H∞优化控制理论[M].哈尔滨:哈尔滨工业大学出版社,2001. [6] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999. [7] 孙增祈.智能控制理论与技术[M].北京:清华大学出版社,1997. 更 正 2013年第4期“基于粒子滤波的红外弱小多运动目标检测”一文的作者单位更正为:国防科学技术大学。 The Simulation and LQ Optimal Controller Design Based on Genetic Algorithm TONG Xin1SONG Zhaoqing2YU Huaguo3 1. Navy Representatives Office in the CALT, Beijing 100076, China 2. Naval Aeronautical and Astronautical University, Yantai 264001, China AkindofLQoptimalcontrollerdesignmethodbasedongeneticalgorithmispresentedaimingatsolvingakindofLQoptimalcontrolproblem.Multipledifferentdesignrequirementsareconvertedintoaninequalityrestriction,andthechoiceproblemoftheweightedmatrixisexpressedtoaproblemofmulti-objectoptimization.Theparametersoftheweightedmatrixareoptimizedbygeneticalgorithm,andthentheoptimalcontrollersatisfyingthecharacteristicrequirementsinfrequency-domainandtime-domainisfoundedatthesametime.Thismethodisappliedtothedesignofoptimalcontrollerforsingleinvertedpendulum,andthesimulationresultvalidatesthatthedesignedcontrollersatisfiesthegivencharacteristicrequirements. Optimalcontrol;Geneticalgorithm;Multi-objectoptimization;Simulation 2013-05-13 童 新(1973-),男,武汉人,工程师,工程硕士,主要研究方向为自动控制、仿真和导弹测发控;宋召青(1969-),男,山东荣成人,教授,博士,主要研究方向为智能控制理论及应用、系统辨识;于华国(1986-),男,山东荣成人,助理工程师,本科,主要研究方向为测试与故障诊断。 TP273.3 A 1006-3242(2013)05-0008-05
3 基于遗传算法的LQ控制器加权阵优化

4 仿真算例
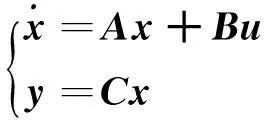
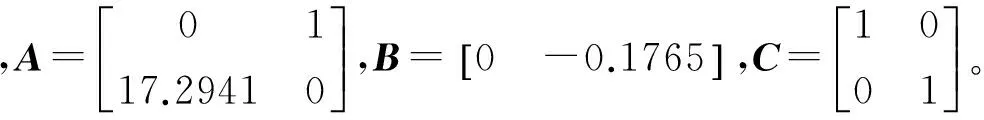
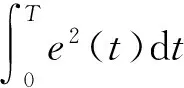
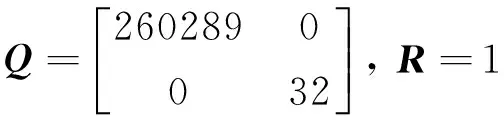
5 小结
3. The 92154thUnit of PLA,Yantai 264001,China
