一种球面点投影关系的推理方法
2013-08-16欧阳继红
欧阳继红,马 玲
(1.吉林大学 计算机科学与技术学院,长春 130012;2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012)
空间推理可以应用到地理信息系统,机器人导航等许多领域。目前,多数模型都是针对二维或三维空间关系的研究[1]。由于实际应用中有时需要直接处理球面上的空间信息[2],如全球变暖的气象分析,全球疾病传播的研究,而二维或三维的空间关系模型以及在此基础上得到的改进模型[3]无法直接应用到球面上,因此,将已有研究推广到球面上建立球面模型,日益受到关注。2005年,Egenhofer[4]将描述拓扑关系的传统9交集模型扩展到球面上。然而,单一的拓扑关系无法较详细地描述空间关系,因此,2006年和2010年Clementini构建了可以同时描述拓扑和方向关系的平面投影关系模型[5],并给出基于此模型的推理系统[6]。2008年,Clementini在此基础上将球面上的空间物体抽象成点,建立了球面点投影关系模型[7](Projective relations among points on the sphere),简称为 PRPS 模型。但是,Clementini只给出了模型的形式表示,未给出推理算法。
为了完善PRPS模型,本文给出了基于PRPS模型的推理算法,通过此推理算法可以由给出的球面投影关系得到未知的球面投影关系。
1 球面属性与PRPS模型
球面异于平面的特性有很多,例如球面上没有直线,可以用大圈来代替,大圈是球面被经过球心的平面截得的圆。对跖点是指两个大圈的交点,有无数个大圈经过。球面上除对跖点外,其他任意两点可以唯一确定一个大圈。
定义1 三元关系指物体A关于物体B和C的关系,用r(A,B,C)来表示。其中B、C为参考物体,A为目标物体,B、C在关系表示中的位置有严格的顺序限制[5]。
定义2 已知三个物体A、B和C经过任意次投影后仍保持共线,则称此三个物体具有共线性[5]。
定义3 投影关系是一种三元空间关系,其中三个物体具有共线性[5]。
投影关系可以描述成“右面”、“之间”、“包围”等。例如,“某城市在北京与上海之间”,“某湖被众山包围”,“某车在交通灯的右边”等。投影关系是一种可以同时描述拓扑与方向关系的空间关系[5]。
1.1 平面点投影关系表达及推理模型
Clementini构建的平面点投影关系模型根据参考点P2、P3的位置关系,将模型分为两种情况:P2、P3是相同点时,将平面分成inside与outside两部分;P2、P3是不同点时,将平面分为rightside,leftside,before,after,between五部分,如图1所示。
Clementini针对平面投影关系模型建立了一个推理系统,类似二元空间关系的逆与复合运算,将其用于构建服务于空间查询的推理系统。因此平面投影关系研究逆、翻转、复合3种运算,具体定义如下[6]:

图1 平面投影关系模型Fig.1 Projective relations model on the plane
定义4 令r(P1,P2,P3)为P1关于P2、P3的投影关系,r1(P1,P3,P2)为P1关于P3、P2的投影关系,称r1(P1,P3,P2)为r(P1,P2,P3)的逆关系,简称为“逆”,记作r︶(P1,P3,P2)。
定义5 令r(P1,P2,P3)为P1关于P2、P3的投影关系,r1(P3,P1,P2)为P3关于P1、P2的投影关系,称r1(P3,P1,P2)为r(P1,P2,P3)的翻转关系,简称为“翻转”,记作r︵(P3,P1,P2)。
定义6 令r1(P1,P2,P3)为P1关于P2、P3的投影关系,r2(P2,P3,P4)为P2关于P3、P4的投影关系,r0(P1,P3,P4)为P1关于P3、P4的投影关系,称r0为r1和r2的复合关系,记作r1◦r2(P1,P3,P4)。
投影关系r的逆关系与翻转关系合称为r的置换关系。
1.2 PRPS模型
Clementini提出的PRPS模型的定义如下[7]:
(1)P2,P3是同一点时
球面被分成两部分,即:点P2(用in(inside)表示)与球面上除点P2的所有范围(用out(outside)表示)。如图2(a)所示。
(2)P2,P3是对跖点时
球面被分成两部分,即:点P2、P3(用in_a(in_antipodal)表示)与球面上除了点P2、P3的所有范围(用out_a(out_antipodal)表示)。如图2(b)所示。
(3)P2,P3是不同点且不为对跖点时
球面被P2、P3所确定的大圈分成两个半球面,将P2P3所在的较短的弧规定为向量P—2P→3,较长弧为 P—3P→2、沿着 P—2P→3上半球面为ls(leftside),下半球面为rs(rightside),所示的弧以及P2和P3两点为bt(between),所示的弧称为notbt(notbetween),如图2(c)所示。
PRPS模型包含8种投影关系:bt,notbt,rs,ls,in,out,in_a,out_a,此关系集合是互斥完备的。
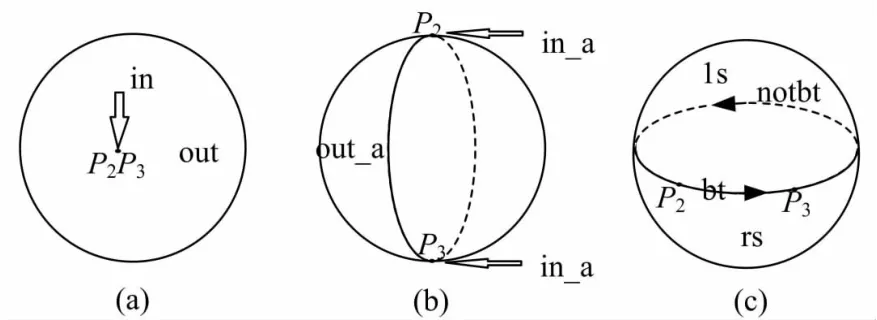
图2 PRPS模型Fig.2 PRPS model
2 基于PRPS模型的推理算法
根据Clementini构建的球面投影关系模型,下面给出基于此模型的推理算法,用于实现由球面物体间已知的投影关系推理出未知的投影关系。
2.1 球面推理与平面推理的异同
与平面推理[6]一样,球面推理也是将对象点用坐标来表示,平面点采用二维坐标(x,y)表示,球面点采用三维坐标(x,y,z)表示。同样根据参考点的连线来划分平面或球面区域,考虑目标点的坐标在某个划分后的区域来确定三点之间的投影关系。
由于球面是一个封闭的面,球面点的投影关系较平面点的投影关系复杂,所以,球面推理与平面推理不同,具有一定的特殊性:
(1)球面上存在对跖点,所以模型需包含参考点为对跖点的情况,推理方法也需考虑此种情况。
(2)当参考点是不同点时,平面所划分的区域除bt外,其他4个区域均为开放区域,而球面所划分的区域都是彼此相连接的,即bt、notbt在同一个大圈上,ls、rs则由一个大圈来连接且区分。
2.2 球面推理算法
推理可以理解成从已有的判断与事实得到新的判断。本文的球面推理过程可以表示为如下过程:

其中P1、P2、P3和P4为球面点,存在的投影关系为r1(P1,P2,P3)与r2(P2,P3,P4);CONVERSE算法、ROTATE算法和COMPOSE算法为推理算法,分别用于求解球面点投影关系的逆关系、翻转关系和复合关系。经过推理算法可以得到P1关于P3、P2的投影关系,P3关于P1、P2的投影关系,以及P1关于P3、P4的投影关系等未知的投影关系。
推理算法的共用子算法为CPRP(Computing the projective relations between points),功能为计算球面三点间投影关系。
下面给出推理算法的主要思想及ADL语言描述。首先作如下说明:球面坐标原点为球心O,球半径为R。球心O、P2、P3确定平面m:z=f(x,y),m 与球面的交线为大圈s:x2+y2+f2(x,y)=R2。point[n]元素为随机球面点。
CPRP算法的主要思想为:
①确定P2、P3的位置关系,查看属于PRPS模型的哪种情况,用type标识。
②根据type的值不同,分别计算P1与P2、P3的球面投影关系,用r来记录。
CPRP算法的ADL语言描述:
CPRP(P1,P2,P3.r)/*P1,P2,P3为球面上三点,r为它们的投影关系*/
C1[确定P2,P3的位置关系]
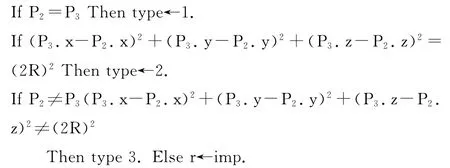
C2[计算P1与P2,P3的球面投影关系r]

CONVERSE算法的主要思想为:
①计算投影关系ri(P1,P2,P3)和ri0(P1,P3,P2)。
②将投影关系ri0记作投影关系ri的逆关系。
CONVERSE算法的ADL语言描述:
CONVERSE(r.r︶)/*r为球面点投影关系,r︶为r的逆关系*/

ROTATE算法的主要思想及具体实现过程与CONVERSE算法类似。
COMPOSE算法的主要思想为:
① 计 算 ri1(P1,P2,P3),ri2(P2,P3,P4),ri0(P1,P3,P4)。
②将ri0记作ri1和ri2的复合关系。
COMPOSE算法的ADL语言描述:

2.3 推理结果
通过CONVERSE算法和ROTATE算法,得到球面点的投影关系r(P1,P2,P3)的逆关系与翻转关系,其置换关系如表1所示。

表1 r的置换关系Table 1 Permutation table for projective relations
下面举一个具体例子来说明表1。
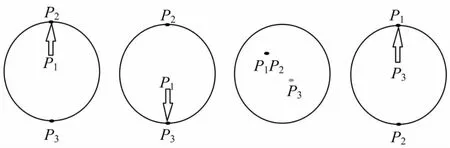
图3 in_a(P1,P2,P3)的逆关系及翻转关系Fig.3 Converse and rotation of in_a(P1,P2,P3)
通过 COMPOSE 算法,得到r1(P1,P2,P3)和r2(P2,P3,P4)的复合关系r1◦r2(P1,P3,P4),如表2所示。

表2 r1和r2的复合关系Table 2 Composition table for projective relations between points
表2中的某些项为imp,是指不存在r1和r2复合的结果,以out(P1,P2,P3)◦notbt(P2,P3,P4)为例,由前者可知P2等于P3,由后者可知P2在P3、P4较长的弧上,P2一定不等于P3,得到矛盾结果,因此这种复合结果一定不存在。
下面举一个例子来说明表2。
例2 r1=ls,r2=rs,其复合的结果是{rs,ls,notbt}(P1,P3,P4)。这是因为P2在P3、P4的rs方向,P1在P2、P3的ls方向,当P1处在球面上不同的位置(例如在的上半球面上,且在的下半球面上,在的上半球面且在的上半球面上,在P3、P4所在的弧上)时,P1相对P3、P4的位置关系则不同。因此,P1关于P3、P4的投影关系或是rs或是ls,或是notbt,如图4所示。

图4 ls和rs的复合结果Fig.4 The composition of ls and rs
2.4 推理性质
对推理算法得到的两个表格进行分析与归纳,可得到如下3个定理。
定理1 {in,in},{out,out},{in_a,in_a},{out_a,out_a},{bt,bt},{notbt,notbt},{ls,rs}为7组互逆关系。
证明 由PRPS模型的定义与球面的对称性可以得到。
定理2 已知投影关系r1(P1,P2,P3),通过置换运算,可得到P1,P2,P3中任意一点关于其他两点的投影关系。
证明 若已知r1(P1,P2,P3),那么r2(P1,P3,P2)即为r1的逆关系,r3(P3,P1,P2)为r1的翻转关系,r4(P3,P2,P1)为r3的逆关系,r5(P2,P3,P1)为r3的翻转关系,r6(P2,P1,P3)为r2的翻转关系,因此经过置换运算,由r1(P1,P2,P3)可推出P1,P2,P3之间所有投影关系,即可推理出-1个投影关系。
定理3 已知投影关系r1,r2和r1◦r2,其中r1◦r2为r1,r2的复合结果,则r1◦r2所属的模型情况与r2的情况相同。
证明 r1表示P1关于P2、P3的投影关系,所属的模型根据P2、P3确定;r2表示P2关于P3、P4的投影关系,所属的模型根据P3、P4确定;r1◦r2表示P1关于P3、P4的投影关系,所属的模型根据P3、P4确定。因此r1◦r2所属的模型情况与r2的情况相同。
由定理1、2和3分别可得到如下3个推理性质。
推理性质1 PRPS模型中投影关系集合{bt,notbt,rs,ls,in,out,in_a,out_a}中存在互逆关系。
推理性质2 置换运算可推理出三点间的任意投影关系。
推理性质3 复合结果具有传递性。
给出投影关系r1(P1,P2,P3)和r2(P2,P3,P4),经过复合运算,可以得到其复合关系r1◦r2(P1,P3,P4),即得到P1关于P3、P4的投影关系,从而将P1、P3和P4间的投影关系联系起来,因此复合推理起到传递的作用,复合结果具有一定的规律可循。
由以上性质可以得出如下结论:PRPS模型中的投影关系集合元素之间存在一定的互逆关系;仅通过置换与复合这两个运算,就能够推理出球面点间的全部投影关系;由于复合具有规律性,根据推理算法得到的结果符合规律,即可知推理结果正确。
2.5 推理应用
PRPS模型可以表达球面对象投影关系,但在某些实际应用的情况下,不能提供进一步指导分析或是推论。例如,在航线部署、灾害预报中经常需要根据一组或两组目标关系,推断出更多对象间的复杂关系,用以指导人类活动,本文的推理算法可以辅助相关部门进行计划部署。
本文推理算法还可以应用到数据库的查询中。类似于二元拓扑关系查询来说,通常已知物体A与B的关系,通过推理算法可以得知物体B与A的关系,而不用再次通过计算获得两者关系。而针对三元物体关系的查询来说,应用本文的推理算法,通过推理性质2和3,得到三者间或更多的物体间的任意投影关系,避免了重复计算。这遵循了建立数据库原则:不用计算物体间的所有完备关系,只需设定一些必要的关系作为主要属性,剩余的关系可以由这些主要属性推导得到,从而节省空间与计算时间。因此,通过前文推理性质及定理可以发现,构建投影关系推理算法是指导实践的重要基础。
3 结束语
针对Clementini建立的PRPS模型仅有表示却无法推理的问题,本文给出了PRPS的推理算法,在理论上使该模型得到完善,在实际应用中可以为进行数据库查询、处理全球气候变化以及为数字地球、飞机导航等做基础理论。推理算法主要有3个,其中CONVERSE算法和ROTATE算法可以计算出球面任意点的投影关系的置换关系,得到置换表。已知一点关于其他两点的投影关系,通过查置换表,可知三点间所有(共6种)投影关系;用COMPOSE算法可以计算出球面点的复合关系,得到8×8项的复合表,通过查表可以由已知的球面投影关系推导出未知的投影关系。并以数据库查询为例,说明了推理算法为此模型在实际问题中的应用奠定了基础。本文的主要工作是将球面上物体抽象成点并进行推理。下一步拟将球面上物体抽象成区域对象,添加形状信息,给出针对区域的球面投影关系的推理算法。
[1]欧阳继红,孙伟,刘大有,等.方向关系矩阵的复合[J].吉林大学学报:工学版,2010,40(4):1048-1053.Ouyang Ji-hong,Sun Wei,Liu Da-you,et al.Com-position of direction relation matrix[J].Journal of Jilin University(Engineering and Technology Edition),2010,40(4):1048-1053.
[2]Tobler W.Global spatial analysis[J].Computers,Environment,and Urban Systems,2002,26:493-500.
[3]欧阳继红,霍林林,刘大有,等.能表达带洞区域拓扑关系的扩展9-交集模型[J].吉林大学学报:工学版,2009,39(6):1595-1600.Ouyang Ji-hong,Huo Lin-lin,Liu Da-you,et al.Extended 9-intersection model for description of topological relations between regions with holes[J].Journal of Jilin University(Engineering and Technology Edition),2009,39(6):1595-1600.
[4]Egenhofer M J.Spherical topological relations[J].Journal on Data Semantics III,2005,2:25-49.
[5]Clementini Eliseoc,Billen Roland.Modeling and computing ternary projective relations between regions[J].IEEE Transactions on Knowledge and Data Engineering,2006,18(6):799-814.
[6]Clementini Eliseo,Skiadopoulos Spiros,Roland Billen,et al.A reasoning system of ternary projective relations[J].IEEE Transactions on Knowledge and Data Engineering,2010,22(2):161-178.
[7]Clementini Eliseo.Projective relations on the sphere[C]∥Proc Second Int'1Workshop Semantic and Conceptual Issues in GIS(SeCoGIS'08).Berlin Heidelberg:Springer-Verlag,2008.
