基于混合整数规划的机场滑行道优化研究

杨守剑

（江苏省交通技师学院，江苏镇江212006）

航班滑行规划是一个存在多种因素制约的复杂问题，受到预计推出时间、滑行道的布局、起飞间隔、出航间隔等因素的影响。近年来, 滑行过程中的不确定性对进离场航班延误的影响日益凸显。一些学者对此进行了一些研究， 他们主要根据给定的飞机滑行路径, 确定飞机经过滑行路径上各点的最佳时间来保证规划期内的机场航班的延误总和最小[1]。但是，所建立的模型没有全面考虑进场航班与离场航班同时运行时滑行道的优化分配方式。

针对上述不足之处，本文在文献[2]的研究基础上，考虑因飞机滑行路线冲突而产生的延误， 同时对其它诸如排序等条件进行综合分析，在基于改进的约束条件的基础上，提出一种进离场航班相互作用的混合整数规划方法。

1 航班滑行优化模型

首先定义以下：

E：两节点之间的有向边集，（vi，vj）∈Ei，i，j＝1，2，…，n；

P：航班集合，D 为离场航班集合，A 为进场航班集合，D∪A＝P；

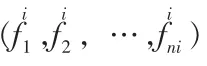
k 为第k 个节点；

PBTi：离场航班i 的推出时间；

SSTi：进场航班i 到达停机位时间；

SATi：进场航班i 计划到达时间；

SDTi：离场航班i 计划起飞时间；

luv：节点u、v 之间的距离；

tiu：航班i 到达节点u 的时刻；

当航班i 先于航班j 到达节点u 时，二元变量ziju=1，否则为0；

我们目的是滑行时间最短，目标函数为：

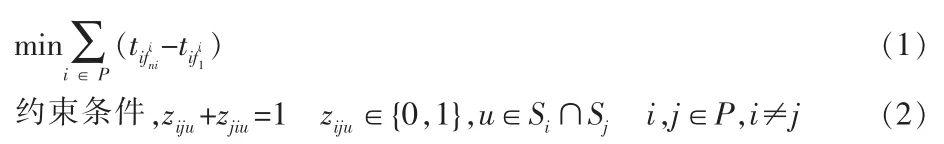
式（2）对航班的顺序进行约束，当航班i 与航班j 的滑行路径同时使用节点u 时，确保任何时刻只有一架航班到达节点u：

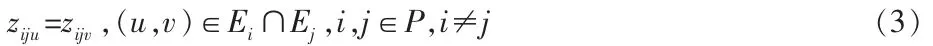
式（3）限制了滑行中航班之间的超越，当航班i 与航班j 同时使用路径（u，v）时，顺序不能改变：

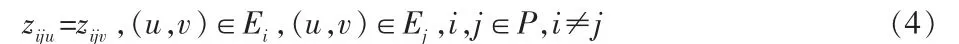
式（4）为交叉限制，当航班i 经过节点u 后到达节点v，航班j 经过节点v 后到达节点u，航班滑行路径不能交叉：

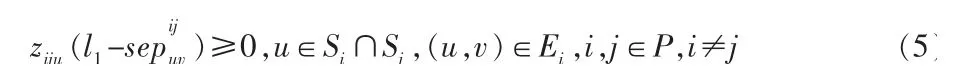
式（5）限制滑行路径中交叉点的最小安全间隔。

设离场航班尾流间隔为Tij，则：

同时考虑最小安全间隔，得到

式（7）、（8）分别限制滑行的起点和终点。

式（9）对滑行速度进行限制。

2 算例验证

为验证优化模型的有效性，使用MATLAB[2]工具对模型进行验证，仿真结果和使用先到先服务算法FCFS 进行了对比。 假设机场跑道长度3800 米，设定25 架航班（13 架重型，12 架中型）在30 分钟内起飞，滑行速度8 米/秒，起飞间隔按照中国民航规定，航班的推出时间间隔由T＝[0，T]进行设置，机场跑道拥挤情况可以由设置T 的大小进行实现。 设置T＝（0，5，10，15，20，25），则两种算法航班平均滑行时间分别为（20，18.1，15.9，14，12.1，9.9）；（13.2，11.3，9.1，7.2，5.4，4.8）。 从上得知，改进的优化模型在不同机场跑道拥挤程度下的平均滑行时间相对于FCFS 算法均实现了减少，且减少的比例都在30%以上。 由此可见，该模型能够有效地节约滑行时间，提高机场的运行效率。

3 结论

本文从机场实际操作的角度出发, 对机场滑行道进行了优化分配。 通过混合整数规划建立了滑行道容量数学模型并使用MATLAB工具对模型进行了验证计算， 在与FCFS 方法得出的结果对比后可知，在同等情况下这种模型的滑行时间得到了减少，效率得到了提高，证明了其优越性和实际可行性。

［1］张莹,胡明华,王艳军.航空器机场地面滑行时刻优化模型研究[J].中国民航飞行学院学报,自然杂志,2006,17(5):3-5.

［2］朱衡君.MATLAB 语言及实践教程[M].北京:清华大学出版社,北京交通大学出版社,2004.