基于数值分析推算船舶航行轨迹算法的实现
2013-08-16肖帅帅
肖帅帅
(上海海事大学商船学院,中国上海201306)
0 引言
船舶航行的轨迹是船东监测船舶营运的重要指标。船舶偏离计划轨迹可能给船舶航行带来危险,然而船舶在海上航行受海浪、海风及海流等环境扰动的影响力作用较大,所以如何对给定的一段航行轨迹有所偏差,在不能及时发觉时,可能会使船舶偏离船舶航行的轨迹。
插值法是一种古老的数学方法,它来自于生产实践。 早在一千多年前,我国数学家在研究历法上就应用了线性插值与二次插值,但它的基本理论和结果却是在微积分产生之后才逐步完善的,其应用也日益增多,特别是在电子计算机广泛使用以后,由于航空、造船、航海等实际问题的需要,使插值法在实践上或理论上显得更为重要,并得到进一步发展,更获得了广泛的应用[1]。船舶AIS 数据大量且长时间保存AIS 信息需要很大的储存空间,这使实时监测航行的轨迹带来很大不便。当只知道船舶航行的几个点后,用插值法推算航行的航迹,船东可以随时观察船舶是否按规定的轨迹航行。监测船舶航迹目的是了解和掌握某个水域内的船舶交通状况和船舶行为规律,通过返回的若干离散的船舶航行轨迹点来绘制船舶航行曲线。 针对此,通过数值分析方法来处理船舶航行返回的离散数据。
针对船舶航行情况,本文在数值分析的基础上,提出一种基于拉格朗日和牛顿差值推算船舶航行的轨迹,仿真实验证明该方法能有效地推算船舶航行中的轨迹。
1 理论分析
1.1 获取船舶位置的AIS 信息
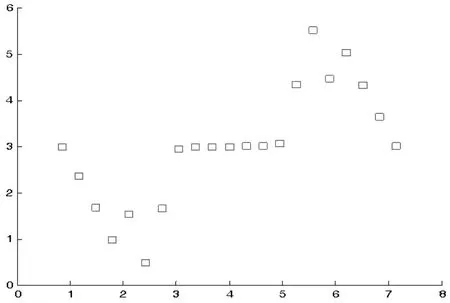
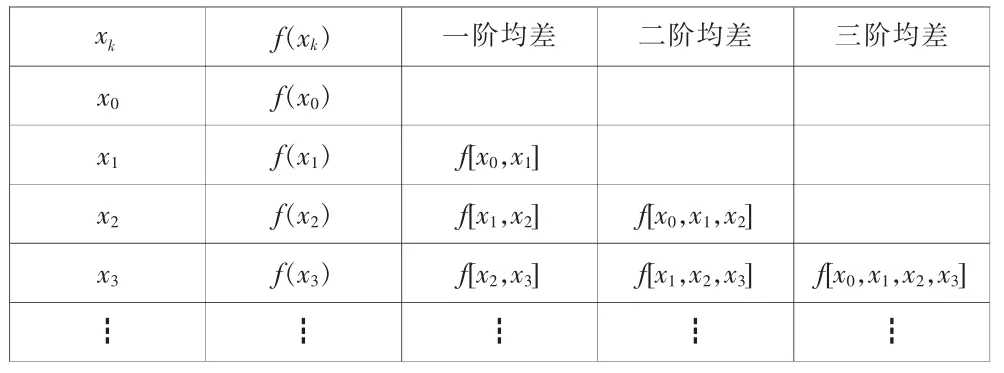
图1 水域中船舶航行轨迹点
AIS 的信息包括静态信息、动态信息、与航次有关的信息、与安全有关的短电文、AIS 船舶报告。主要使用静态信息和动态信息。动态信息包括船位及其精度标示和完好性状态;协调世界时UTC 标记的定位时间、船舶的对地航向(COG)、对地航速、航行状态和旋回速率。 其中包括交通流量、速度和占有率。 主要包括海上移动通信业务标识(mmsi)、航速(speed,单位“kn”)、经度(lon,单位“′”)、纬度(lat,单位“′”)、艏向(heading,单位“(°)”)、船长(length,单位“m”)、船宽(width,单位“m”)[7]。
显然,船舶的航行曲线是一条连续不间断的航线。 因此在给定的一个区域内船舶航迹虽只给出一些离散点(如图1 所示),我们仍可通过数值分析中的插值法来推算完整的航迹。
图1 为船舶在水域返回的若干航行轨迹点,对此数据下面我们引入拉格朗日插值法来处理。
1.2 拉格朗日插值简介
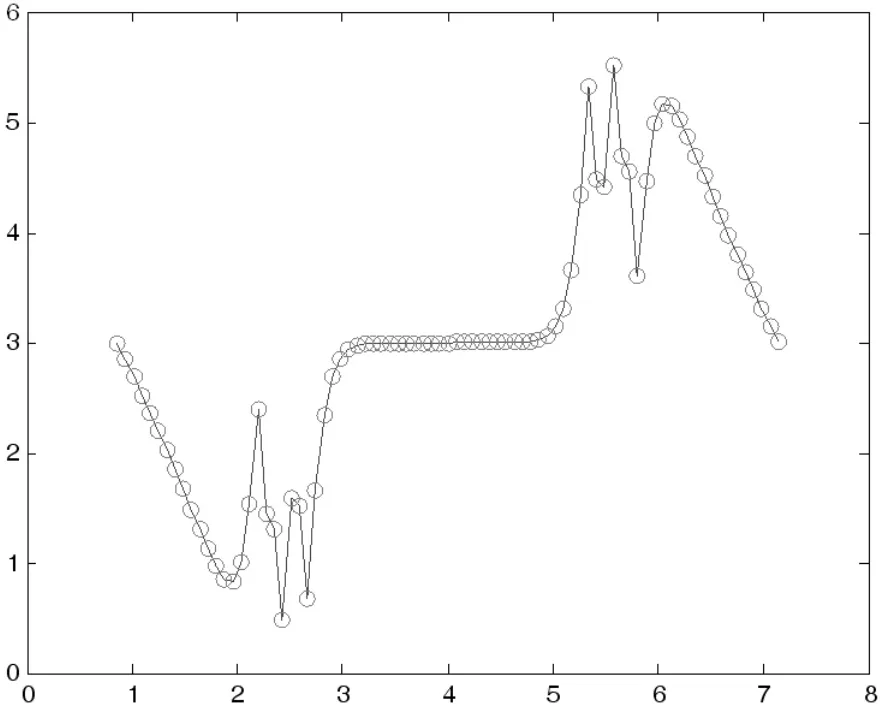
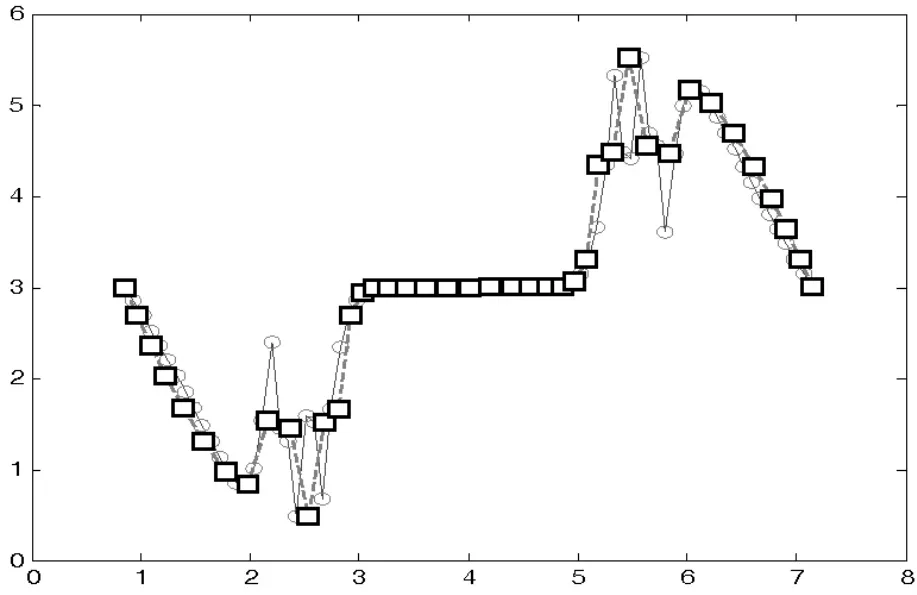
设函数y=f(x)在区间[a,b]上有定义,且已知在点a≤x0<x1<… 成立,就称P(xi)为f(x)的插值函数,点x0,x1,…,xn称为插值节点,求插值函数P(xi)的方法称为插值法。 若P(xi)是次数不超过n 的代数多项式,即 就称P(xi)为插值多项式。 图2 水域中船舶航行轨迹线 从几何上看,插值法就是求曲线y=P(xi)使其通过给定的n+1 个点(xi,yi),i=0,1,…,n,并用它近似已知曲线y=f(x)。 下面给出拉格朗日插值公式: 其中 ωn+1(x)=(x-x0)(x-x1)…(x-xn) 利用已知的船舶航行数据节点,根据拉格朗日插值法可绘制出如图2 曲线[5]。 考虑在一个固定的区域内插值去逼近船舶的航行路线,显然拉格朗日插值中使用的点越多,插值多项式的次数就越高。 而并不是因此绘制出的航迹就越准确,同时随着插值节点的增多,需要记录存储的船舶航迹点就越多。 下面是Runge 给出的一个例子。 考虑在区间-1≤x≤1 上的函数: 构造等距节点上的拉格朗日插值多项式。当插值节点的个数增加时,插值多项式的次数随之而增加。 在Matlab 上运行程序可发现当插值节点增多时,实验结果并非越来越好,这一现象如今已得到越来越多人的关注。 值得提出的是,随着船舶返回的节点的增加,又得重新进行拉格朗日插值工作,计算量可想增大。 因此在拉格朗日插值的基础上引入牛顿插值来解决这一缺憾。 利用插值基函数很容易得到拉格朗日插值多项式,担当插值节点增加时全部插值基函数均要随之变化,整个公式也将发生变化,这在实际计算中很不方便,为了克服这一点,可把插值多项式表示如下便于计算的形式: 其中a0,a1,…,an为待定系数,可有插值条件确定。 表1 均差表 根据均差定义,把x 看成[a,b]上的一点,可推得牛顿均差公式为[4]: Nn(x)=f(x0)+f[x0,x1](x-x0)+…f[x0,…,xn](x-x0)…(x-xn-1) 图3 水域中船舶航行轨迹线 它比拉格朗日差值计算量省,且便于程序设计。 对于船舶航行提供的若干点可以方便的绘制出船舶航行曲线, 同时当节点增加时,前面的工作可以为后面的计算提供帮助,大大节省了计算量。 而对于插值结果,它们两个所得到的船舶航行轨迹线是是相同的,如图3 所示。 检测精度的计算公式:中误差按下列公式计算。 式中:M检——中误差 n——检测点数 △——平面较差 选取实际部分点与插值生成后的点数据误差比较如表2: 表2 误差统计表 由此可以看出牛顿插值可以用来较好的推算船舶运行航迹。 实际船舶航行的曲线与经过牛顿插值推算后的曲线比较如图4。 图4 航行轨迹与推算航迹 本文对船舶航迹推算所涉及到的数值分析方法进行了分析和论证,设计了基于插值法对船舶航行轨迹推算算法。 理论分析了插值法解决这一问题的关键点及误差分析,并给出了相关公式,对相关理论进行了Matlab 仿真,通过分析得到以下结论:拉格朗日插值法在处理船舶航行节点时有简单之处,但随着节点数的增加,计算量也大大增加。 运用牛顿插值推算船舶航迹相比拉格朗日差值计算量大大减小,而且有较高的精度,得出了数值分析推算船舶航行轨迹的可行性。 可以推算船舶航行过的航迹,船东可以根据少量的数据点,清晰地了解船舶在海上运动的连续轨迹,并且也可以根据它推算出船舶在继续航行的前方是否存在危险,对事故的鉴定与预防有很重大的意义。 用此方法推算船舶航行轨迹有重大的参考意义。 [1]李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2007. [2]吴兆麟.海上交通工程[M].大连:大连海事大学出版社,2004. [3]白峰杉.数值计算引论[M].北京:高等教育出版社,2004. [4]李庆扬,关治,白峰杉.数值计算原理[M].北京:清华大学出版社,2000. [5]刘卫国.MATLAB 程序设计与应用[M].北京:高等教育出版社,2006. [6]李庆扬,关治,白峰杉.数值计算原理[M].北京:清华大学出版社,2000. [7]林袆珣.数据挖掘技术在海上交通特征分析中的应用研究[D].集美大学,2011,6.


1.3 误差估计
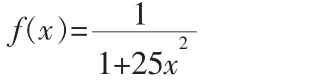
2 牛顿插值
2.1 均差
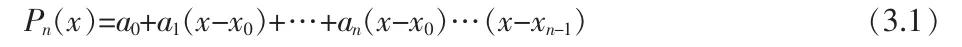
2.2 牛顿插值公式
2.3 精度检验


3 结论
