开关状态函数化及其在多电平逆变器分析中的应用

刘汉阳 黄松清

（安徽工业大学电气信息学院，安徽 马鞍山 243002）

电力电子技术是21世纪最有潜力、应用最为广泛新兴技术之一[1]。但是电力电子装置应用到的开关器件均工作在非线性状态，使得对其分析一直停留在定性的阶段，这也成为电力电子技术应用的瓶颈。常规的开关模型没有完整描述电力电子装置的能力，在分析上多采用仿真结合实验的对比和推演分析，并不能全面揭示出装置内部的工作规律，总有管中窥豹之感。在这种分析方法下，大量数学工具无法得到应用，给控制算法的优化研究带来了很大困难，同时也造成了电力电子装置的设计和改进多依靠经验。

PWM 控制方法目前为止是众多电力电子装置对开关器件的控制方法。在仔细分析众多的PWM控制算法后，能够发现它们仍存在一些共同的问题：

1）控制算法繁多，有些算法大同小异，研究上有一定的盲目性。

2）各种算法直接存在内在联系，但目前并没有人在数学层面上对其进行完整的揭示，致使算法研究存在重复性。

3）对各种优化算法优劣的评判标准主要靠仿真和实验验证，缺少系统的量化分析。

缺少一种统一的分析工具是导致这些问题的重要原因，本文提出一种将开关状态函数化的分析方法，巧妙地将数学分析工具引入到电力电子技术的分析过程中。找出了函数化后的电力电子装置定义域，将输出定义为所需要的 PWM信号。因此，可以将已有的 PWM控制算法用开关状态函数的形式统一的表达，并以此产生输出信号；也可以根据装置输出指标要求得到控制所需的 PWM信号。可见此方法可对各种 PWM控制算法进行统一分析，简化研究的复杂度。最后将这种全新的分析方法应用到多电平逆变器的分析之中。

1 开关状态函数

将电力电子装置中的一个或几个开关器件在某一时刻整体的开通关断状态定义为电力电子装置的开关状态S。无论电力电子装置采用何种电路拓扑结构，在某一时刻经开关器件变换输出的电压都至少对应一种开关状态，而某一时刻每个开关状态只对应一种输出电压。由此可见开关状态是时间的函数，而装置的输出电压是开关状态和时间的函数

在这种情况下去推导输出电压的解析式并不容易，因为即使开关状态一定，电压依然是时间的函数，可能会随时间变化。但当变换装置的电源为稳定直流时，装置只能靠不同开关组合产生有限种输出电压，此时输出电压是幅值离散的连续信号，一种开关状态只能对应一种输出电压。在实际应用中控制系统多为数字系统，在每个控制周期里装置输出为一组电压序列，第n个控制周期的输出电压可表达为

式中，Ts为系统控制周期，m是开关状态的数量，AnS是开关状态S在第n个控制周期里的作用区间，可通过计算机或者微控制器离线或在线计算得到。

利用式（2）可得出在连续时间上输出电压的表达式

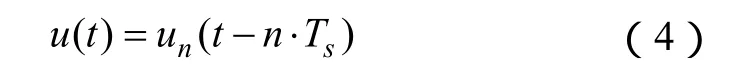
式（2）和式（4）即为变换装置输出电压的开关状态函数表达式，可见开关状态函数相当于一种基函数，任意波形的输出电压均可以由开关状态函数的组合来表达。不同的控制算法的区别仅仅在于AnS的计算方法不同，所以可以基于开关状态函数对各种控制算法进行统一地分析并得出开关器件的控制信号，这就是开关状态函数的分析方法。可见开关状态函数特别适用于分析那些对直流电源进行变换的电力电子装置。

对得到电压序列表达式的过程进行逆向思考，可知能够在已知电压序列的情况下得到与之对应的开关状态分布情况，由此在实际设计中我们就可以根据装置期望的输出要求得到开关器件的控制信号。装置的一种电压输出可能对应了多种开关状态，所以设电压Um对应的开关状态集合为Sm。定义函数为

通过式（5）即可由装置的输出电压得到相应的开关状态的集合，进一步要根据系统要求的控制目标来合理地选择开关状态，此过程即为上面开关状态函数化表达的逆过程。至此通过开关状态函数建立了装置的输出电压和开关状态之间较为完整的关系，二者的互逆关系给系统的分析和设计带来了很大方便。

下面利用开关状态函数的分析方法对图1所示电路做简要分析。此电路即为基本的Buck变换电路，电路有两种开关状态，可定义S的定义域为{0, 1}，0表示开关导通1表示开关关断。若控制周期为0.002s，占空比为0.5，输出电压为

由开关状态函数得到系统输出电压的准确表达式，则负载电流可充分利用系统分析的方法来求解。

图1 Buck变换电路

基于基尔霍夫回路方程，可得电路微分方程为

易求电流的冲击响应h(t)，则系统的零状态响应为激励函数u(t)与h(t)的卷积

将系统离散化，则式（7）改写为差分方程的形式有

x(nT)是输出电压u(t)的采样序列，y(nT)是负载电流序列。

同样有式（8）的离散形式

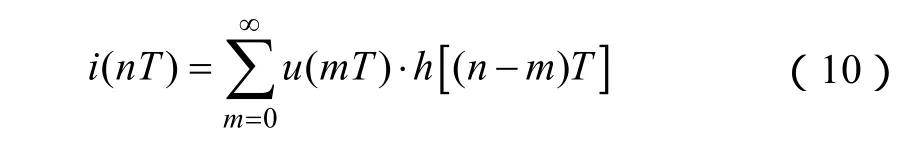
减小样值时间T，利用计算机可以较为精确的求解式（9）和式（10）。

可见利用开关状态函数得到电力电子装置输出电压表达式后，可以较为方便的引入传统系统分析方法对输出进行分析。将表达式离散化后，可以方便的利用计算机对各表达式进行数值求解，也可进一步对信号进行变换和分析，方法的通用性较强。

2 开关状态函数在多电平逆变器分析中的应用

多电平逆变器具有输出电压电流谐波小、降低器件的电压应力和耐压等级要求等优点，因而在高压调速、静止无功补偿等多个领域得到应用[5-7]。多电平逆变器的 PWM控制技术一直是多电平逆变技术的研究重点之一，但长期以来并没有一种分析方法能够对现存的方法进行统一的分析和比较。这导致了在实际应用中控制算法选择和实现的困难，同时也造成了PWM算法研究的重复性和盲目性。文献[3]利用开关状态函数对三电平逆变电路进行了分析，但所提方法不能简单有效的分析更多电平的电路。下面提出一种更有效的开关状态函数的分析方法，对多电平逆变器进行分析并提出一种根据输出要求得到三电平开关序列排布的简易方法和一种逆变器输出谐波的计算方法。

2.1 多电平逆变器的开关状态函数

设逆变器直流母线电压为UDC，由图2可得对于一个m电平逆变器，每一级电平值为

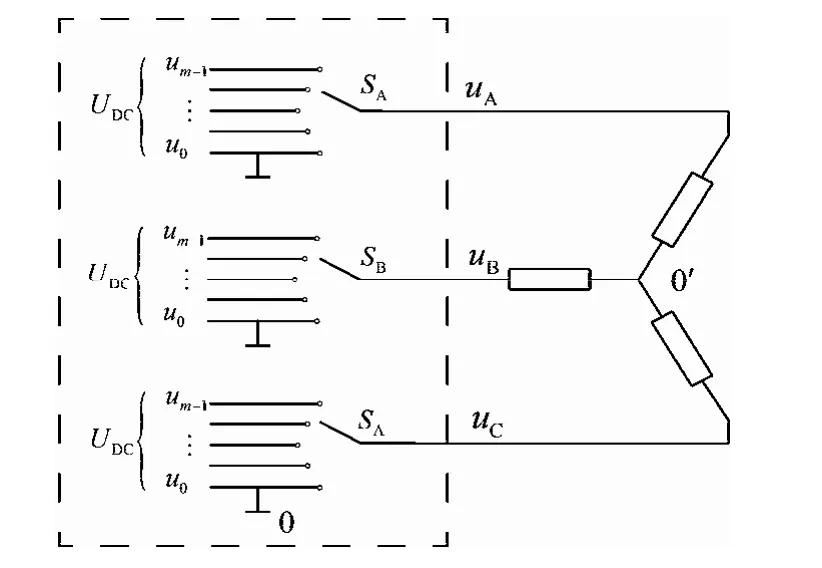
图2 多电平逆变器开关模型

则每一相可以输出的电平为0，E，2E，…，(m-1)E。定义逆变器输出电压的最低电位为参考零点0，0′为三相对称负载的中点，三相开关状态为Sa，Sb，Sc，则逆变器三相输出电压为

在三相负载平衡的情况下负载的相电压之和为0，将式（14）各项相加得

将式（15）代回式（14）中，可得

将式（11）带入式（12）和式（16）中并将其改写成矩阵形式可得逆变器输出相电压和负载相电压关于开关状态的函数

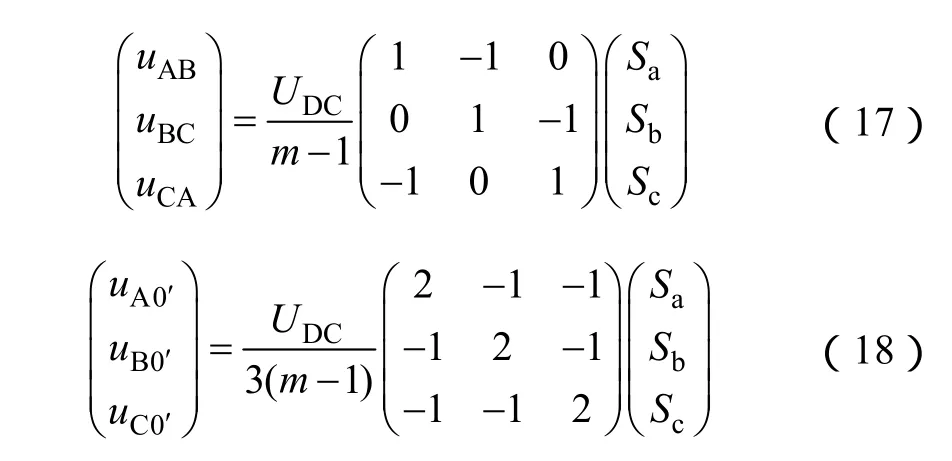
开关状态与电压空间矢量之间也有着密切关系。定义m电平电压空间矢量关于开关状态的函数为

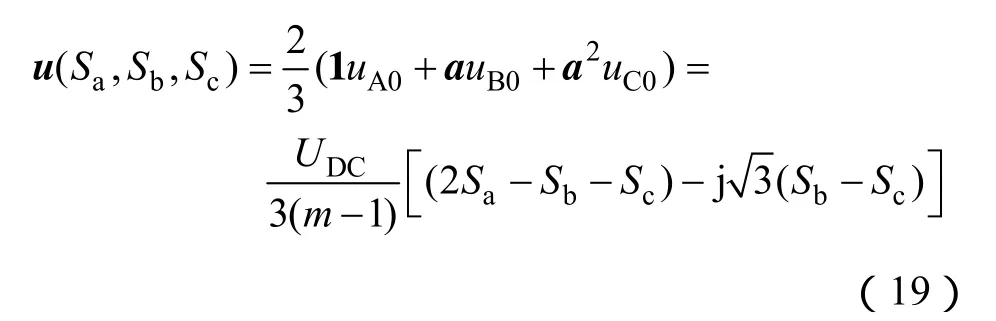
图3 三电平逆变器的电压空间矢量与开关状态

式中，1=ej0°、a=ej120°、a2=ej240°分别为A相、B相和C相电压的单位空间矢量。由此定义可得到多电平逆变器输出电压的空间矢量图。如图3所示空间电压矢量图中的每一个顶点都是一种独立的电压空间矢量，总数为3m(m - 1)+1。而逆变器的开关状态共有m3种，除了最外侧的空间矢量外，其它空间矢量都对应了多种开关状态，此即开关状态的冗余。进一步分析可知开关状态的冗余的本质是叠加在线电压上的共模电压，冗余状态间有如下关系，即

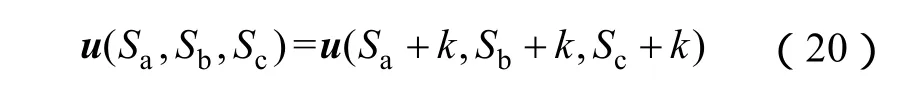
式中，k为开关状态冗余系数。

由以上分析可以得多电平逆变器的开关状态与逆变器输出电压以及空间电压矢量有着简单的线性映射关系，因此开关状态函数可以作为多电平逆变器的有力分析工具。事实上在数字系统中，载波调制法多采用对称规则采样，在每个采样周期里逆变器三相输出电压都是关于Ts/2对称的电压序列。在上面的分析中指出，在这种调制方法下各种PWM控制方法的差异仅仅是电压序列中各个电压（也即开关状态）的作用时间的计算方法不同，这就为用统一的分析方法去分析不同的控制方法提供了可能性。

2.2 一种三电平开关序列排布的简易方法

多电平逆变器的 PWM控制法主要可分为载波调制法，消除特定谐波法（开关点预置 PWM法）和空间电压矢量调制法。基于这三种 PWM控制算法，针对不同的电路结构和要求，又可以派生出许多具体优化的多电平PWM控制法[6-9]。这些算法实际上是逆变器输出电压序列排布方法有所不同，也即开关序列排布方法不同。

将开关状态函数化后可以揭示出一些普通分析方法较难发现的控制规律。下面提出一种根据输出要求得到三电平开关序列排布的简易方法。

设图3中由电压矢量000、100、110的顶点围成的三角形为ΔABC，以参考矢量Uref位于ΔABC区域里的情况为例。此时根据NTV法则（Nearest Triangle Vectors）需利用UA、UB、UC三个电压矢量根据秒伏平衡的原理来合成Uref。开关状态的排布要满足两个基本原则：每个采样周期内开关状态序列应历遍三种电压矢量；每次开关状态切换时只能有一位改变且只变化一级。这保证了每次切换只有一个桥臂上的开关动作从而降低开关频率，同时杜绝了电源正负极直通的情况。将含有“0”的开关状态排在最底层，在式（20）中令k从零开始增加依次向上排列出其他的冗余状态，则三个电压矢量的开关状态排列成图4的形式。此时只要选择一个开关状态作为起点沿图4中所示路径按一个方向变化即可快速查找出所有满足以上两个基本原则的开关序列，进一步可根据不同的控制目标对开关序列进行选择。此方法适用于任意电平逆变器的分析，尤其当电平数增加时开关状态冗余进一步增多，用此方法来排布开关状态可大大降低工作量。

图4 开关序列排布方式

以三电平二极管钳位电路的中点电压作为附加控制目标说明此方法的应用。按照电压矢量的幅值一般可将三电平电压空间矢量分为4类：零矢量、短矢量、中矢量、长矢量。电路输出零矢量和长矢量时电容上没有电流流过，所以二者对中点电压没有影响。中矢量的开关状态没有冗余，但中矢量自身对中点电压偏移有平衡作用。每个短矢量对应两个开关状态，且这两个开关状态对中点电压的影响是相反的。因此通过在一个开关序列周期里排布两个对中点电压起相反作用的短矢量开关状态可达到修正中点电压偏移和抑制中点电压波动的目的[10-11]。仍以上述ΔABC区域为例，若采用七段式矢量合成方案，则一个开关序列周期里要包含UB或UC的两个开关状态。利用图4可得出4种可选方案。

1）选择100为起点：

100—110—111—211—111—110—100

2）选择211为起点：

211—111—110—100—110—111—211

3）选择110为起点：

110—111—211—221—211—111—110

4）选择221为起点：

221—211—111—110—111—211—221

对于方案1）来说，结合中点电压和中点电流的方向合理分配开关状态100与211的作用时间即可达到对中点电压平衡控制的目的，其他方案同理。有关各矢量作用时间计算以及分配的问题国内外学者已提出了多种方法，这里不再赘述[10-14]。

2.3 开关状态函数化方法应用—逆变器输出谐波分析

以三电平逆变器为例，为减小开关损耗令uA0、uB0、uC0在一个采样周期里一般最多跳变两次。

则A相在一个采样周期里输出电压序列为

根据式（21）可知一个完整的2π电角度周期内，逆变器输出电压表达式为

对u(t)做周期拖延后得到的周期函数显然满足Dirichlet条件，则可对输出电压进行Fourier级数展开

根据式（18）可推得A相负载相电压的n次谐波的幅值为

利用式（23）、（24）、（25），借助计算机可以比较简单准确的计算出逆变器输出电压序列的各阶谐波幅值。

3 仿真结果

Simulink RTW（Real-TimeWorkshop，新版Simulink中称为 Simulink Coder）可以从Simulink模块、Matlab函数搭建的仿真模型生成目标芯片的可执行代码，并在Simulink与目标芯片间建立通信路径从而实现在Simulink平台上结合外部实物系统进行包括半实物实时仿真等多种仿真功能，这大大提高了验证算法可行性的速度，缩短了系统开发的周期。为方便用户使用RTW生成TI DSP C2000系列芯片的可执行代码，TI公司与Mathworks公司联合开发了Target Support Package TC2软件包并DSP C2000系列芯片中的各个部分抽象封装成Simulink模块形式。

本系统运用Simulink搭建了三相钳位式三电平逆变器，依据上文所提方法编写了基于C语言的S-function实现了一种带有中点点位平衡功能的三电平SVM 算法和谐波计算算法，并利用Simulink RTW和Target Support PackageTC2实现了仿真与DSP芯片间的耦合，令仿真更具现实意义。仿真参数如下：直流电源电压600V，钳位电容470μF，调制度0.8，输出电压频率50Hz，仿真采样时间1×10-6s，控制周期2×10-4s，三相对称RL负载：R=10Ω，L=0.1H。图5（a）、（b）、（c）、（d）分别为逆变器输出的线电压、负载相电压、负载电流和中点电压的仿真波形。可见负载相电压在任何时刻没有发生超过两个电压阶梯的跃变，负载电流较接近正弦波，中点电压的波动幅度控制在5V以内。表1为计算得到的负载相电压奇次谐波的幅值。可见算法较好的实现了三电平SVM算法且具有平衡中点电压的能力。系统设计采用ICETEK-F2812-A评估板实现控制部分，评估板硬件结构如图6所示。DSP2812包含两个独立的EV模块，每个模块可输出三路两两互补的 PWM波形。程序设计中对两个EV模块进行统一配置，使12路PWM信号同步工作，对电路中12个开关器件进行控制，达到了充分利用DSP片上资源的效果。

图5 仿真波形

表1 负载相电压谐波幅值

图6 ICETEK-F2812-A评估板硬件结构

4 结论

本文通过分析总结传统电力电子分析方法的弊端，提出了一种开关状态函数的分析方法，巧妙地将数学分析工具引入到电力电子技术的分析过程中，力图从数学上做到对电力电子装置较为完整且统一的分析。因此，可以根据传统的 PWM技术，得到多电平PWM控制信号；也可以根据逆变器输出要求得到控制需要的 PWM信号。通过利用此方法对多电平逆变器的分析以及仿真实现验证了方法的可行性和有效性。开关状态函数的分析方法提供了一种运用数学手段完整描述电力电子装置的途径，为将更多的数学工具引入分析和优化工作中奠定了基础。

[1]陈坚.电力电子学—电力电子变换和控制技术[M].2版.北京:高等教育出版社，2004.12.

[2]黄松清.电压型变频器—三相交流异步电动机传动系统的稳定性[J].控制理论与应用,2005,22(2):223-228.

[3]赵圣宝,黄松清,胡寅峰.基于开关状态函数化的三电平逆变器分析及仿真研究[J].电气技术, 2010(6).

[4]孙长冬，黄松清，刘绪良，等.一种改进的七电平逆变器对比仿真研究[J].电气技术, 2010(1).

[5]NABAEA,TAKAHASHII,AKAGIH.A new neutral-point clamped PWM inverter [J]. IEEE Trans.Ind. Applicat., 1981, IA-17(5): 518-523.

[6]LAI J S, PENG F Z. Multilevel inverters: A new breed of power converters[J]. IEEE Transaction on Industry Application, 1996, 32(3): 509-517.

[7]刘凤君.多电平逆变技术及其应用[M].北京:机械工业出版社, 2007.4.

[8]姜卫东,王京群,陈权.一种完全基于两电平空间矢量调制的三电平空间矢量调制算法[J].电工技术学报, 2009, 24(1): 108-114.

[9]HOU X, LI Y D, LIU Y H. A novel general space vector modulation algorithm for multilevel inverter based on imaginary coordination[C]. PEDS’03 Record,2003: 201-207.

[10]宋文祥,陈国呈,武慧,等.一种具有中点电位平衡功能的三电平空间矢量调制方法及其实现[J].中国电机工程学报, 2006, 26(12): 95-100.

[11]SHEN J, STEFAN S, ROBERT R. A comprehensive study of neutral-point self-balancing effect in neutral-point-clamped three-level inverters[J]. IEEE Transactions on Industry Applications, 2011, 26(11):3084-3095.

[12]窦真兰,张同庄,凌禹.三电平NPC 整流器空间矢量脉宽调制及中点电位平衡控制[J].电力自动化设备, 2008, 28(2): 65-69.

[13]宋强,刘文华.基于零序电压注入的三电平 NPC逆变器中点电位平衡控制方法[J].中国电机工程学报,2004, 24(5): 58-62.

[14]宋文祥,陈国呈,束满堂,等.中点钳位式三电平逆变器空间矢量调制及其中点控制研究[J].中国电机工程学报, 2006, 26 (5): 105-109.