中长期电力负荷的灰色残差修正组合预测

卢建昌 裴乐萍

（华北电力大学经济管理系，河北 保定 071003）

电力负荷预测作为电力系统规划的基础，提供着电力增长、负荷曲线以及电力分布的各方面信息。它是电力系统规划和运行中的重要工作之一[1]。而随着我国市场经济的完善和发展，电力市场由垄断变为竞争，对负荷预测的精度产生了更高的要求。如何根据负荷实时变化规律实现负荷的实时预测是负荷预测工作的核心与难点。根据负荷的实时变化规律进行预测就要从负荷本身的走向趋势出发，根据曲线的走向将负荷曲线分为不同的阶段，根据不同的阶段分别建立模型，然后组合预测。

针对中长期电力负荷预测样本少，贫信息和不确定性，基于灰色理论的预测更具有适用性。但是，由于灰色模型的预测本身不适用于S型曲线，而中长期电力负荷趋势大都呈S型。本文根据曲线特点分为两个不同的阶段，第一阶段在饱和阶段建立模型，在不能达到后验差检验的一级精度要求后，采用残差修正的灰色模型预测，第二阶段建模已经达到了一级精度要求，直接采用灰色模型预测。两个阶段根据事中检验精度比例分配不同的权重，按照精度分配权重能够充分保证预测的准确性。整个过程进行组合预测，对不符合精度要求的阶段进行改进，实例证明的此组合方法提高整体的预测精度。

1 灰色预测理论

1.1 灰色GM(1,1)预测建模

灰色系统理论最早由我国学者邓聚龙教授于1982年提出[2]。GM(1,1)模型是最常用的一种灰色模型，它是由只包含单变量的一阶微分方程所构成的模型，是GM(1,n)模型的特例[3]。

设有X（0）为原始序列

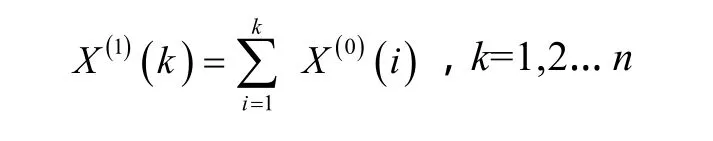
则称｛X（1）｝为｛X（0）｝ 的累加数列，数据处理后，即可建立一阶微分方程：

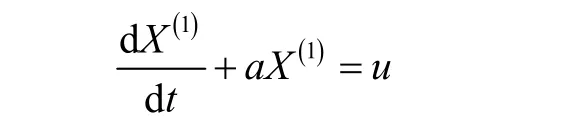
式中，a为发展系数；u为灰作用度。可根据最小二乘法求得模型参数：

将此式累减生成还原，则可得到关于原始数据序列的灰色预测模型：

1.2 后验差检验

灰色模型的建模优劣精度通常用后验差检验方法进行。它根据残差ε绝对值的大小，考察残差较小的点出现的概率，以及与预测误差方差有关指标的大小[4]。

记k时刻实际值与预测值之差为ε（k），成为k时刻的残差：

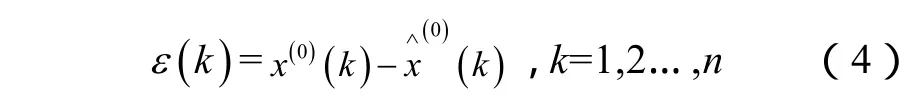
其中，指标C越小越好，指标P越大越好。按C和P两个指标，可以综合评定预测模型的精度。

1.3 残差修正GM(1,1)模型

当后验差检验不符合要求时，此时就不能用灰色GM(1,1)预测模型进行预测，这就造成了灰色GM(1,1)预测模型的局限性。为了克服这种局限性，扩大灰色预测模型预测的范围，本文采用残差修正的方式修正残差[5-6]，并将残差与原来的灰色GM(1,1)预测模型相结合，构造出新的预测模型。残差修正GM(1,1)预测模型为

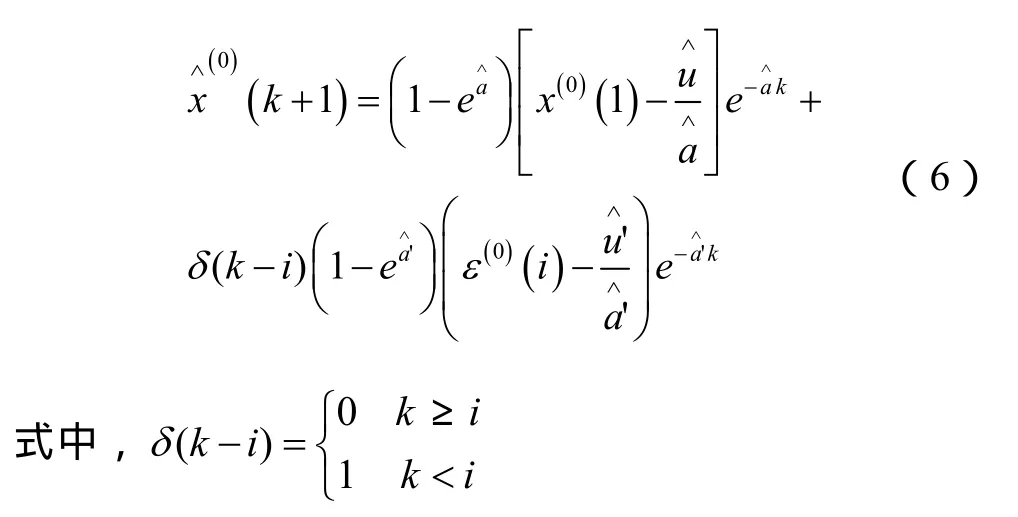
若不满足，则重新选择残差序列，继续修正。

2 灰色残差修正组合预测

2.1 分阶段建模

灰色预测应用到中长期电力负荷预测时，会出现增长率过快的问题，因此需要对灰色GM(1,1)预测模型进行改进，目前，对灰色GM(1,1)预测模型的改进主要基于两方面，一是对于原始数据的预处理，二是对于模型本身进行改造[7]。但是这两方面都没有考虑负荷数据本身的发展趋势，没有根据具体的负荷数据走向特点进行预测。本文的组合预测一方面针对负荷数据走向特点进行分阶段建模，另一方面对模型本身进行改造，避免了传统模型进行中长期负荷预测的缺陷，同时也对具体负荷数据特点的考虑。从负荷走向的固有规律出发，对一条曲线的负荷预测可以分阶段预测[8]，每个阶段采取适合于该阶段的预测模型，然后组合成新的预测模型。

2.2 组合预测

阶段划分之后就要考虑不同阶段的权重分配问题。组合预测[9-10]是基于不同阶段的模型的基础进行预测。组合预测的关键是关于权重的确定。权重有不同的确定方法[11]。为了更好的提高预测精度，本文权重的确定依据模型事中检验精度的比例进行分配。根据不同阶段模型的平均精度，进而求得不同阶段模型的权重。具体实现过程如下：

记α(k)为残差相对值，有

式中，i代表第i个模型，n为模型个数。本题划分为两个阶段预测，则最终组合预测模型为

3 算例应用

为了验证残值修正组合预测的可行性和适用性，现有唐山市农村实际用电量数据见表1。

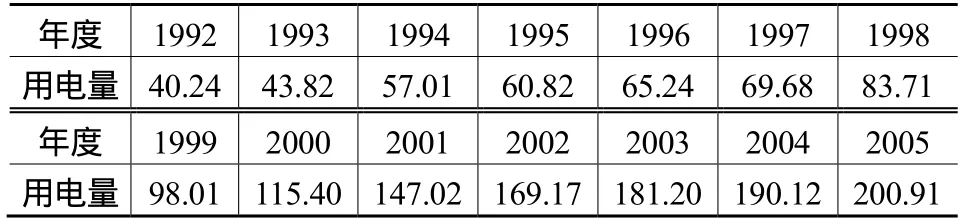
表1 唐山市1992－2005年农村用电量单位：亿kW·h

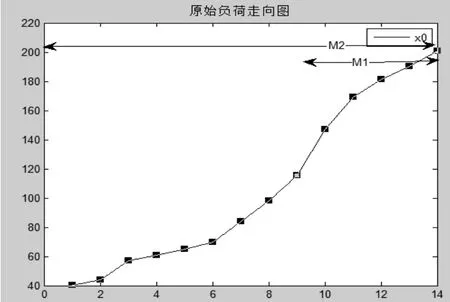
图1 原始负荷走向图

如图1所示，首先根据图形的特点划分为不同的阶段。根据负荷曲线特点，负荷从开始进入饱和状态为一个转折点，因此可将负荷曲线划分为两阶段M1和M2，如图1所示。首先要分别用GM(1,1)模型对M1和M2阶段进行初步的负荷预测，进而进行后验差检验。预测结果显示M2预测阶段C2=0.17，P2=1，预测精度达到一级，因此用GM(1,1)模型对M2阶段预测能够达到比较好的效果。M1阶段整体不呈现指数增长形势，而是逐渐饱和的形态，若直接采用灰色模型，C1=0.38，P1=0.83，精度为二级，不能达到一级要求。为提高M1阶段预测精度，需对传统的灰色模型进行改进，增加残差修正，从而降低预测误差。

M1和M2阶段模型平均精度p1=0.926，平均精度p2=0.9779，则w1=0.49，w2=0.51。最终得到使用于本数据变化特点的组合预测模型如下：

表2 实际值与预测值比较

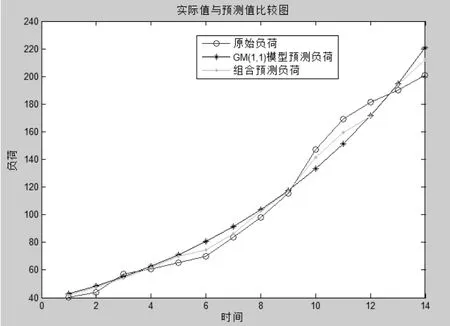
图2 实际值与预测值比较图

组合预测后的相对误差明显比组合预测前的相对误差降低，预测精度明显提高。由图2可以看到，组合预测负荷拟合曲线能更好的反应原始负荷曲线的走向和趋势，能够随着原始负荷的走向变动而变动。而传统的GM(1,1)预测拟合曲线只能粗略的反应负荷曲线的大体方向，而负荷的波动变化未能较好的拟合。结果表明残差修正组合预测能够较好提高预测精度。

4 结论

灰色预测方法作为电力系统负荷预测的方法虽然已经很成熟，但是由于其有应用的局限性，限制了它在电力负荷预测中的应用范围。一般来说，原始负荷数据若不满足指数增长规律，采用灰色预测方法预测误差会大大增加，预测结果也不能反映负荷变化趋势。而从负荷数据本身的曲线所反映的特点出发，根据曲线特点划分为不同阶段，进而分配权重进行组合预测，能够避免负荷数据因指数增长造成的误差。

[1]牛东晓,曹树华,赵磊.电力负荷预测技术及其应用[M].北京：中国电力出版社,1998.

[2]邓聚龙.灰色预测与决策[M].武汉:华中理工大学出版社,1992.

[3]张俊芳,吴伊昂.基于灰色理论负荷预测的应用研究[J].电力自动化设备,2004(5).

[4]卢建昌,牛东晓.电力企业管理[M].北京:中国电力出版社,2007:301.

[5]牛勇,王震宇,王红军,等.改进灰色模型在中长期电力负荷预测中的应用[J].东北电力大学学报,2009, 29(2):64-68.

[6]范鹰,郭建伟.灰色模型在电力负荷预测中的应用与改进[J].电力需求侧管理,2006,8(2).

[7]俞明生,冯桂宏,杨祥.组合优化灰色模型在中长期电力负荷预测中的应用[J].沈阳工业大学学报, 2007,29(2):153-156.

[8]张志明,金敏.基于灰关联分段优选组合模型的短期电力负荷预测研究[J].电工技术学报,2009,24(6):115-120.

[9]李建伟,赵法起,刘凤玲.中长期电力负荷的组合预测法.电力系统及其自动化学报,2011,23(4):133-136.

[10]徐聪颖,廖峰,陈震海.灰色组合模型在中长期电力负荷预测中的应用[J].电力需求侧管理,2011,13(2).

[11]黄元生,张惠娟.灰色关联度组合权在电力负荷预测中的应用[J].华东电力,2009,37(2).