《淮南子》中的“量天尺”

王永礼

（淮南师范学院 物理与电子信息系，安徽 淮南 232038）

一、引言

《淮南子》是由西汉淮南王刘安及其宾客编著的，成书年代大约在汉景帝、武帝之间。刘安是一位多才多艺的人，他既是诸侯王，又是文学家、思想家、科学家，也是神仙道家，他甚至是发明豆腐的美食家①陈丽华：《〈淮南子〉研究初探》,《蓝台世界》2007年10月下半月，第45－46页。。

与《淮南子》关系最密切的是淮南国与淮南王刘安。没有淮南国就没有淮南王,没有淮南王刘安就没有《淮南子》。汉高帝四年,刘邦把九江大郡(此郡统辖江淮之地和长江以南大部分地区)改制为淮南国,并封九江王英布为淮南王,辖九江、庐江、衡山、豫章四郡。这也是历史上“淮南”一词第一次被用于行政地域名称。辖区涉及现今皖、赣、豫、鄂、湘五省。汉文帝时又将淮南国分为庐江、衡山、淮南三个小国。汉武帝元狩初年,因刘安谋反获罪，淮南国被废,恢复九江郡,至此淮南国的历史结束，共有81年。淮南国的国都、九江郡的首府都在寿春(现在安徽省的寿县)②方川：《〈淮南子〉与“淮南学”》,《淮南师范学院学报》2007年第 6期，第 14－16页。。

《淮南子》是汉代学者对汉朝以前古代文化最大规模的汇集与融合,内容十分丰富,书中大量吸收和发展了先秦、秦汉时期道家、法家等学说,内容涉及哲学、社会科学、自然科学等各个领域。

二、《淮南子》的宇宙观

对于宇宙的形成，《淮南子》认为：“道始于虚廓,虚廓生宇宙,宇宙生元气,元气有涯垠,清阳者薄靡而为天,重浊者凝滞而为地,清妙之合专易,重浊之凝竭难,故天先成而地后定。”（《淮南子·天文训》）这种对宇宙起源的看法，与现今最流行的大爆炸理论也有些相似之处，并可与毕达哥拉斯的宇宙观念相媲美③李晓林：《〈淮南子〉中的宇宙起源思想》,《陕西教育学院学报》1997年第2期，第56页。。

《淮南子》对宇宙万物演化生息的自然图景表现出了浓厚兴趣，还穷究天地剖判万物生化的自然奥秘。而且，它还吸收了当时天文学发展的最新成就，以阴阳五行思想，构筑了一幅完整的宇宙形成、结构及衍化总图景，而这一宇宙总间架成为其后两千多年宇宙演化生成论的最权威“蓝本”④唐劭廉，吕锡琛：《〈淮南子〉自然观：继承和超越》,《船山学刊》2003年第4期，第114－117页。。

《淮南子》的自然观念中体现了自然的创造性，崇尚道法自然，在其思想体系中,视天地为生养自然万物之父母,包括人类①章晓丹：《〈淮南子〉的自然价值观》,《华中科技大学学报》（社会科学版）2007年第6期，第84－87页。。《淮南·天文训》对于宇宙的形成、组织、结构等有着深入的论述,尤其对三光特别关注。三光又称三辰,即日、月、星②陶磊：《〈淮南子〉与古代数术》,《徐州师范大学学报》(哲学社会科学版)2005年第2期，第73－77页。。并且它还根据三光的测量，对于天有多高,地有多大进行了详细的论述和计算，对后世有着深远的影响。

三、天高的测量

《淮南子》对于天地的认识为：“天道曰圆,地道曰方；方者主幽,圆者主明。”即天圆地方说。它认为大地是平直的，天在大地上方，日在天穹上，因而可以通过测量日的高度来确定天的高度。其测量时所使用的长度单位有里、丈、尺、寸。“十寸而为尺,十尺而为丈。”（《淮南子·天文训》）

《淮南子》提出测量天高的方法为：

“欲知天之高,树表高一丈,正南北相去千里,同日度其阴。北表一尺,南表尺九寸,是南千里阴短寸。南二万里则无景,是直日下也。阴二尺而得高一丈者,南一而高五也,则置从此南至日下里数,因而五之,为十万里,则天高也。若使景与表等,则高与远等也。 ”（《淮南子·天文训》）

在这一段叙述中，《淮南子》总共提供了三种测量天高的方法。

（一）三角函数法测量天高

《淮南子》提出测量天高的第一种方法：“欲知天之高,树表高一丈,正南北相去千里,同日度其阴。北表一尺,南表尺九寸,是南千里阴短寸。”

据此叙述可绘出测量图如图1，图中AB为高为一丈的表尺竖直设立在B处，CD也是高为一丈的表尺竖直设立在D处，D处在B处的正南方一千里。在正午时同时进行测量，若AB表尺的阴影长A'B为一尺，而CD表尺的阴影长C'D为9寸。据此就可算出天高RO的数值H。

在直角三角形A'AB和直角三角形A'RO中：

在直角三角形C'CD和直角三角形C‘RO中：

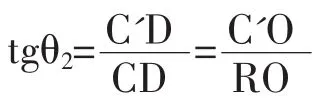
因为：AB=CD=h，RO=H

代入数据：S0=1000里，h=10尺，A'B=1尺，C'D=0.9 尺

可得：H=1000×10/(1－0.9)(里)

=100000(里)

=10万里

即日高为10万里。

（二）相似三角形法测量天高

《淮南子》给出的第二种测量天高的方法：“南二万里则无景,是直日下也。阴二尺而得高一丈者,南一而高五也,则置从此南至日下里数,因而五之,为十万里,则天高也。”

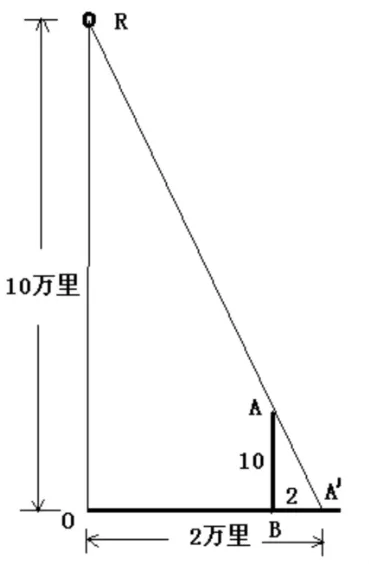
图2 《淮南子》测量天高的方法（二）示意图

据此叙述可绘出测量图如图2，图中高一丈的表尺AB，其阴影A'B长为二尺，若表尺AB正南方二万里处竖直表无阴影，此处即为太阳的正下方O点，由于表高是阴影的5倍，因此日高也是距离A'O的5倍，即10万里。这里就是使用了两个相似三角形的对应边成比例的数学关系。

因为：ΔA'BA与ΔA'OR相似

即此方法测量的日高为10万里。

（三）等腰三角形法测量天高

《淮南子》提出的第三种测量天高的方法为：“若使景与表等,则高与远等也。”

图3 《淮南子》测量天高的方法（三）示意图

据此叙述可以绘出图3。图中AB是竖直放置的表尺，A'B是其阴影，若A'B与AB等长为h，则三角形A'BA就是等腰直角三角形。再利用相似三角形法，若O点是太阳的正下方，则三角形A'OR也是等腰直角三角形，于是：

因此只需要测量标尺的这种放置点B，与其正南方表尺无阴影的放置点O之间的距离，就可得到太阳的高度了。

四、讨论

由于当时的人们还没有认识到大地是一个球面，而把大地看成是无限平直的，这是一个错误的观点，在这个错误的基础之上的计算，其结果可想而知都是错误的。但是《淮南子》给出的测量天高的方法，从数学方面看是完全正确的。它不仅显示了当时人们已经掌握了高深的数学知识，而且这些知识在实际的生产实践中也可得以应用。比如测量高大建筑物的高度，或者测量高大树木的高度等，都可以使用上述方法。