四象限非对称风场对风暴潮的改进研究

傅赐福，于福江，2，刘秋兴，李涛

（1.国家海洋环境预报中心，北京 100081；2.国家海洋局海洋灾害预报技术研究重点实验室，北京 100081）

台风风暴潮是我国频发的重大海洋灾害，其造成的经济损失从20世纪90年代后已有明显增加的趋势，风暴潮的预报及研究是海洋防灾减灾的重要研究课题。经过国内外众多学者几十年的研究揭示了风暴潮发生的主要机制和一般规律，总的而言，风暴潮是气象因素占主导、多种海洋要素综合作用的结果，包括风、气压、天文潮、近岸海浪、河口径流等，风暴潮与海洋各要素的耦合作用在近海尤为复杂。

风场作为引发风暴潮的主要因子，对风暴潮预报和研究起到关键作用。到目前为止，人们只能利用有限的手段去研究台风风压场，归纳起来，主要有三大类：第一类是圆对称风场模型（高桥，1939；藤田，1952；Jelesnianski，1965；Holland，1980）；第二类为改进的非对称风场模型，如非对称结构风场模型（章家彬等，1986），椭圆形对称的风压模型（陈孔沫，1994），特征等压线风场模型（朱首贤等，2003）；第三类为气象数值预报模型，如MM5，WRF。这三类风场模型对台风风压场的刻画各有优劣：第一类模型便于描述计算，但未能客观反映不同类型台风的风压场结构特征；第二类模型则要考虑天气形势、时空变化，较难去定其经验参数；气象数值预报模式对初始场资料要求较高，且空间分辨率较低，台风路径和强度预报也有待进一步提高。

随着风暴潮预报往精细化发展，更准确风场的获得成为了一个重要研究方向，本文将引入一个基于Holland模型风场改进的四象限非对称模型风场，并参考美国NOAA热带气旋实时产品提供的7级、10级、12级风圈资料，利用ADCIRC模型建立的高分辨率风暴潮模式对1117号热带气旋“纳沙”引起的强风暴潮进行数值模拟，对比四象限风场和Holland风场对风暴潮改进效果并分析结果。

1 四象限模型风场

1.1 Holland模型风场

Holland模型风场是较常用的台风模型风场（Holland et al，1980），台风气压场分布见公式（1）：

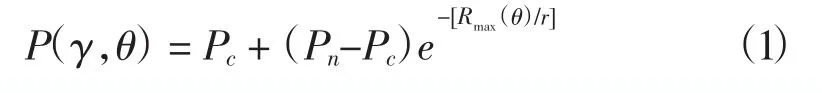
其中，P（γ，θ）是距台风中心γ处的海表面气压值，为径向距离γ、方位角θ的函数；Pc为台风中心气压，Pn为台风以外不受干扰的背景气压，取为1 012百帕；Rmax是台风最大风速半径，为方位θ角的函数。

在Holland台风风场的计算中，假设梯度风平衡，即气压梯度力、离心力与科氏力的平衡所得到切向风速，见公式（2）。

其中，V（γ）为距离台风中心的切向风速，ρa为空气密度，f为科氏参数；B是台风轮廓参数，表征台风眼区直径和切向速度梯度，一般取值1.0～2.5。该模型计算得到的风场是轴对称的，在台风移动方向的右半圆科氏力作用使得切向风速加强，左半圆切向风速减弱。

1.2 四象限非对称风场模型

而实际上，大部分的热带气旋风场结构是非对称的，这样的热带气旋在靠近或者登陆时会对风暴潮预报带来较大误差。而如果能将所观测较精确的风场资料分为四个象限使我们构造出来的风场更接近观测，就能进一步减少预报误差。Xie等（2006）提出了四象限非对称风场模型，具体的风场构造及计算如下：

假设已知1117号强台风“纳沙”实况见表1。为了易于求解，将Rmax写成方位角θ的多项式函数，见公式（3）。

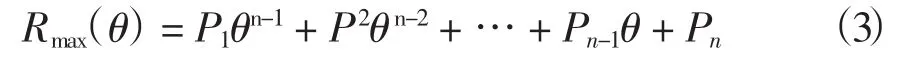
对于公式（2）中，已知实况点的信息，在Vmax=V(γ=Rmax)的情况下（Vmax是最大风速），可得：

对于某个象限的风力（例如7级）的风圈半径是已知的，利用公式（2）即可求解得到Rmax。通过每个象限算出的Rmax（共4个）代入公式（3）中，其中n=5，通过多项式拟合即可求解出P1、P2、P3、P4、P5，这样就可以求得距离台风中心任意位置点的风速。由于每个象限某个风力风圈半径不尽相同，因此所计算的风场分布是非对称的。

表1 1117号热带气旋“纳沙”某一时刻的风场特征信息

2 风暴潮模式及数据来源

2.1 ADCIRC风暴潮模式

ADCIRC模式是基于有限元方法的跨尺度（大洋、近岸、河口）水动力计算模型，采用非结构三角形网格（Westerink et al，2006）。通过基于垂直平均的原始连续方程和运动方程来求解自由表面起伏、二维流速等3个变量，在球坐标系下，连续方程和运动方程可表示为：初始条件为：ζ=u=v=0；海岸边界条件为：边界的法向速度为0；

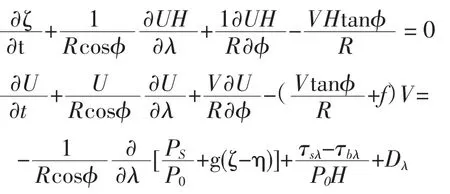
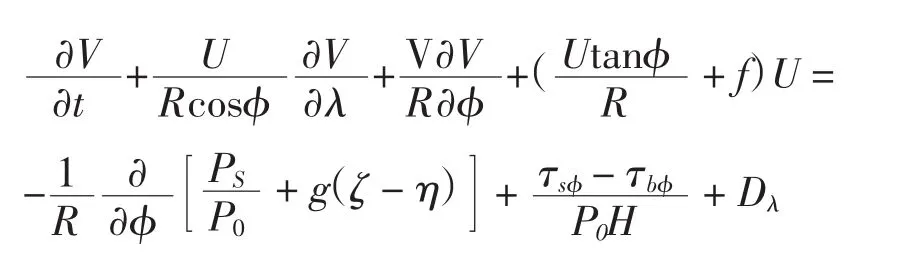
开边界条件：静压边界；

模式中求解所需物理变量的过程中，空间采用有限元法离散，时间采用有限差分法。将连续方程和运动方程通过引入空间变量数值加权参数进行结合求解，提高了计算结果的稳定性，时间步长取为20 s；

底摩擦力与深度平均流呈二次平方律关系，底摩擦系数采用线性与二次律混合形式；海面风应力与风速呈二次平方律关系，风拖曳系数采用Garratt公式，Cd=0.001×（0.75+0.667）×W，（2‰≤Cd≤3‰）。

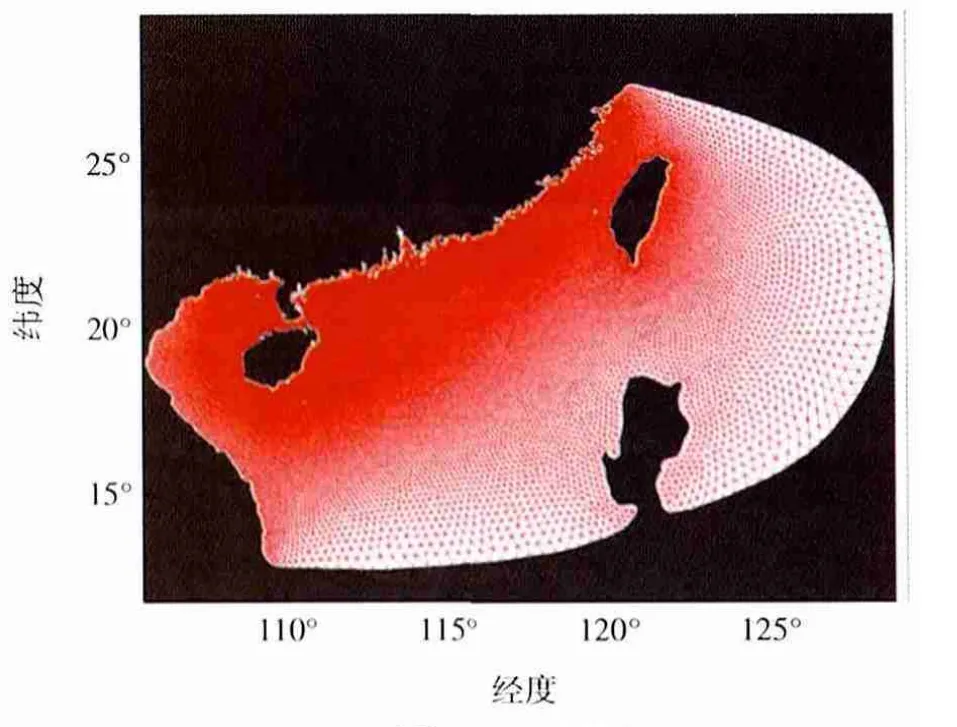
图1 计算区域网格划分

模型的计算区域及网格分布见图1所示，计算区域包括了东海南部和大部分南海，开边界网格分辨率为20～30 km，除粤西的近海网格分辨率为1～4 km，粤西近海网格分辨率为0.4～0.8 km，整个计算区域包括121 880个计算格点，236 554个计算单元。

2.2 台风数据来源

文中四象限台风资料采用美国国家飓风中心（NHC）的热带气旋最佳路径资料，该资料同化了被动微波传感器资料（Special Sensor Microwave Imager，简称SSM/I）、快速遥感主动散射计数据（Quick Scatterometer，简称SCAT）、微波探测风场数据（Advanced Microwave Sounding Unit，简称AMSU）等海面观测风场资料（Mueller et al，2006）。目前，NHC所提供的热带气旋最佳路径资料（包含四象限风圈半径预报信息）已被美国海洋与大气管理局（NOAA）业务化使用。

文中的另一个风场Holland模型的资料也是取自NHC的热带气旋最佳路径资料。这样可以客观地比较两种不同模型风场对风暴潮的影响。

3 1117“纳沙”风暴潮模拟分析

3.1 1117“纳沙”概况

2011第17号强台风“纳沙”（NESAT）于2011年9月24日上午在西北太平洋洋面上生成，9月26日夜间和29日7时两度加强成为强台风，并以强台风的强度于29日14时30分前后在海南文昌市登陆，29日21时前后在广东徐闻再次登陆，是2011年登陆我国强度最强的台风。受其影响，9月28日至30日，从广东省、海南省、广西省沿海先后出现了一次强风暴潮过程，广东三灶、闸坡、湛江、南渡、海南秀英潮位站均出现了超过当地警戒潮位的高潮位，以上三省直接经济损失超过30亿元。图2为9月29日-30日上午的台风路径、验潮站和浮标分布及关心区域水深分布。

3.2 风暴潮模拟

利用已建立的风暴潮模式，分别用原Holland模型风场和四象限非对称模型风场驱动计算风暴潮进行对比分析。

图3和图4分别为珠海、台山、海安、秀英、水东、硇洲、湛江、南渡等8个潮位站模拟与实测的对比图，表1为各站模拟最大风暴增水与实测的对比及误差。从图和表中可以看出，位于雷州半岛东岸的水东、硇洲、湛江、南渡潮位站在两种风场的驱动下模拟风暴潮曲线、最大风暴增水数值均相差不大，与实测值接近；而位于珠江口东岸和琼州海峡的潮位站在四象限风场的驱动下模拟效果明显优于原Holland风场驱动，更接近实测值，原Holland风场驱动的最大风暴增水平均相对误差为23.3%，而四象限风场驱动的最大风暴增水平均相对误差仅为5.4%。

3.3 风暴潮模拟差异分析

图2 关心区域水深、“纳沙”路径（紫）及所涉及验潮站、浮标（红）示意

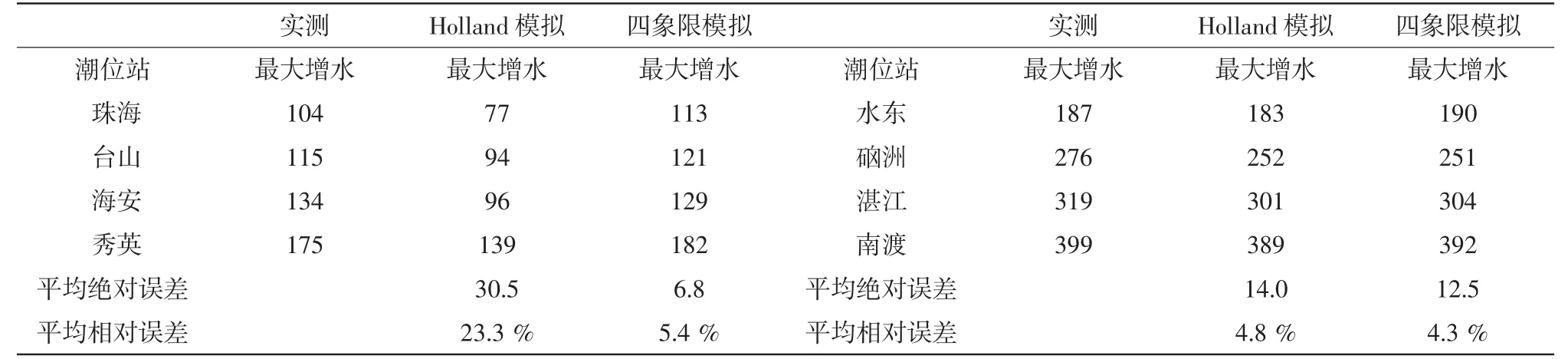
表2 各站最大风暴增水模拟与实测对比（单位：cm）

“纳沙”是较典型的西北路径影响粤西的热带气旋，在500 hpa高空图天气形势是副高稳定地位于热带气旋的北侧，反映在地面天气图上是热带气旋的北侧为高压控制，因此此路径下热带气旋东北和西北象限的风力及风圈往往要比东南和西南大。

为了考察风暴潮差异的原因，本文选取了广东近海3个浮标的风资料进行对比，这3个浮标均位于“纳沙”路径的北侧（详见图2），图5为其在两个风场模型输出风速、风向与实测的对比。从图中可以看出，通过同化更多风场资料的四象限风场参数所构造的风场在“纳沙”路径的北侧得到了加强，无论风速还是风向均比Holland模型构造得到的风场更加接近实测值。

此外，为了全面考察两种风场模型构造风场对风暴潮的差异，本文选取了最大风暴增水出现时段、即恰好也是台风登陆前和登陆后陆后的两个时次（29日14时和29日18时），考察上述两种风场模型构造的台风风场差异及对风暴潮引起的差异。

图6为29日14时和29日18时两个时次两种模型构造的风场、风暴潮差值（四象限-Holland）。从图6a、图6b和图6c、图6d来看，四象限模型所构造的风场在西北和东北象限的风圈明显大于Holland模型且呈现出明显的非对称性，即西北和东北象限比西南和东南象限的风力和风圈明显要大。从图6e和图6f来看（四象限-Holland的风暴潮差值，在这段落简称“风暴潮差值”），在“纳沙”登陆前（29日14时），在珠江口到珠江口以西、海南省东北部沿海风暴潮差值为0.2～0.4 m；在“纳沙”登陆后（29日18时），在珠江口到珠江口以西沿海的风暴潮差值减小为0.1～0.3 m，在琼州海峡附近沿海的风暴潮差值增加为0.3～0.5 m；而在粤西到雷州半岛东岸沿海的风暴潮差值几乎为0。这些变化反应在潮位站的时间序列上正如图3和图4所示。

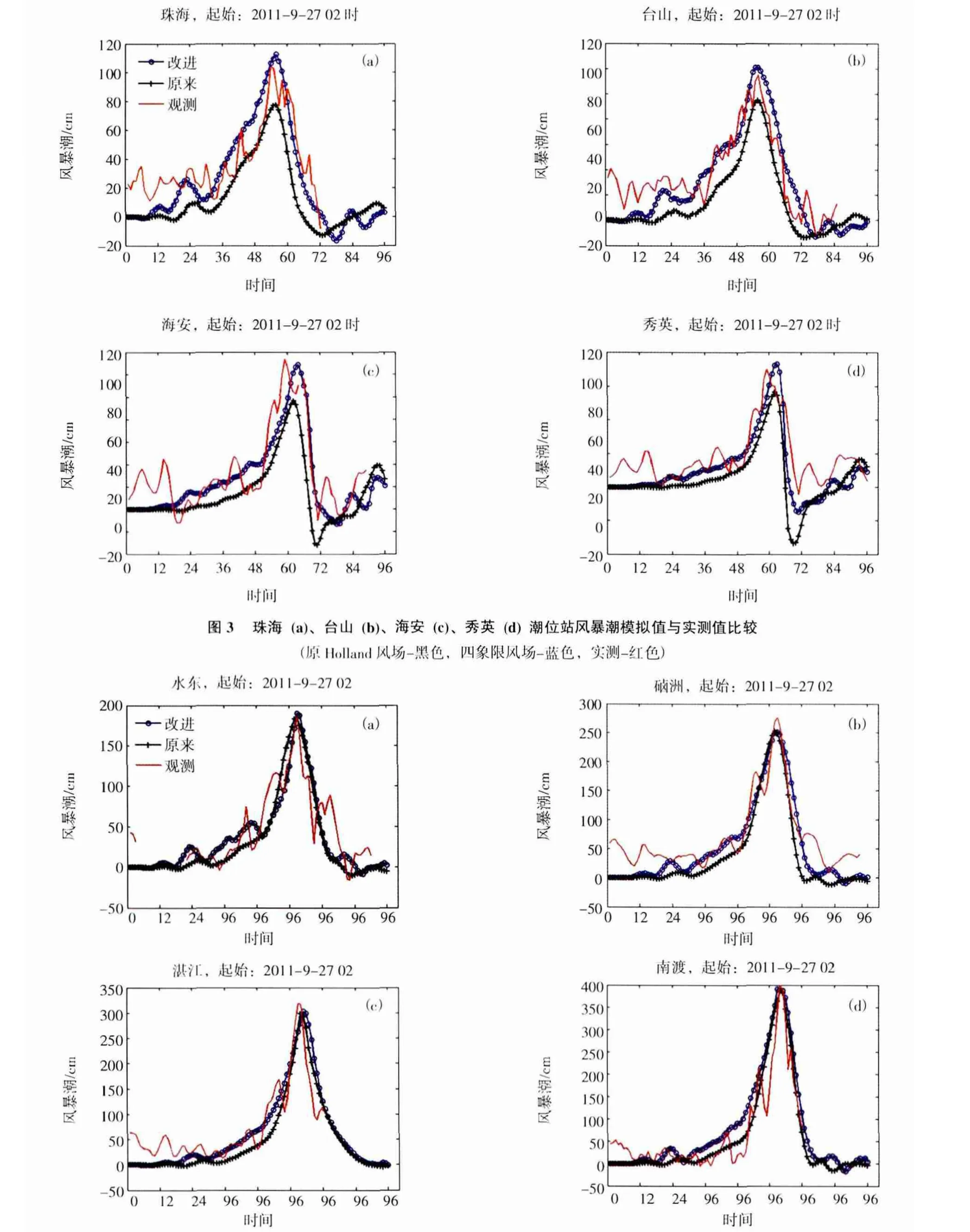
图4 水东（a）、硇洲（b）、湛江（c）、南渡（d）潮位站风暴潮模拟值与实测值比较（原Holland风场-黑色，四象限风场-蓝色，实测-红色）

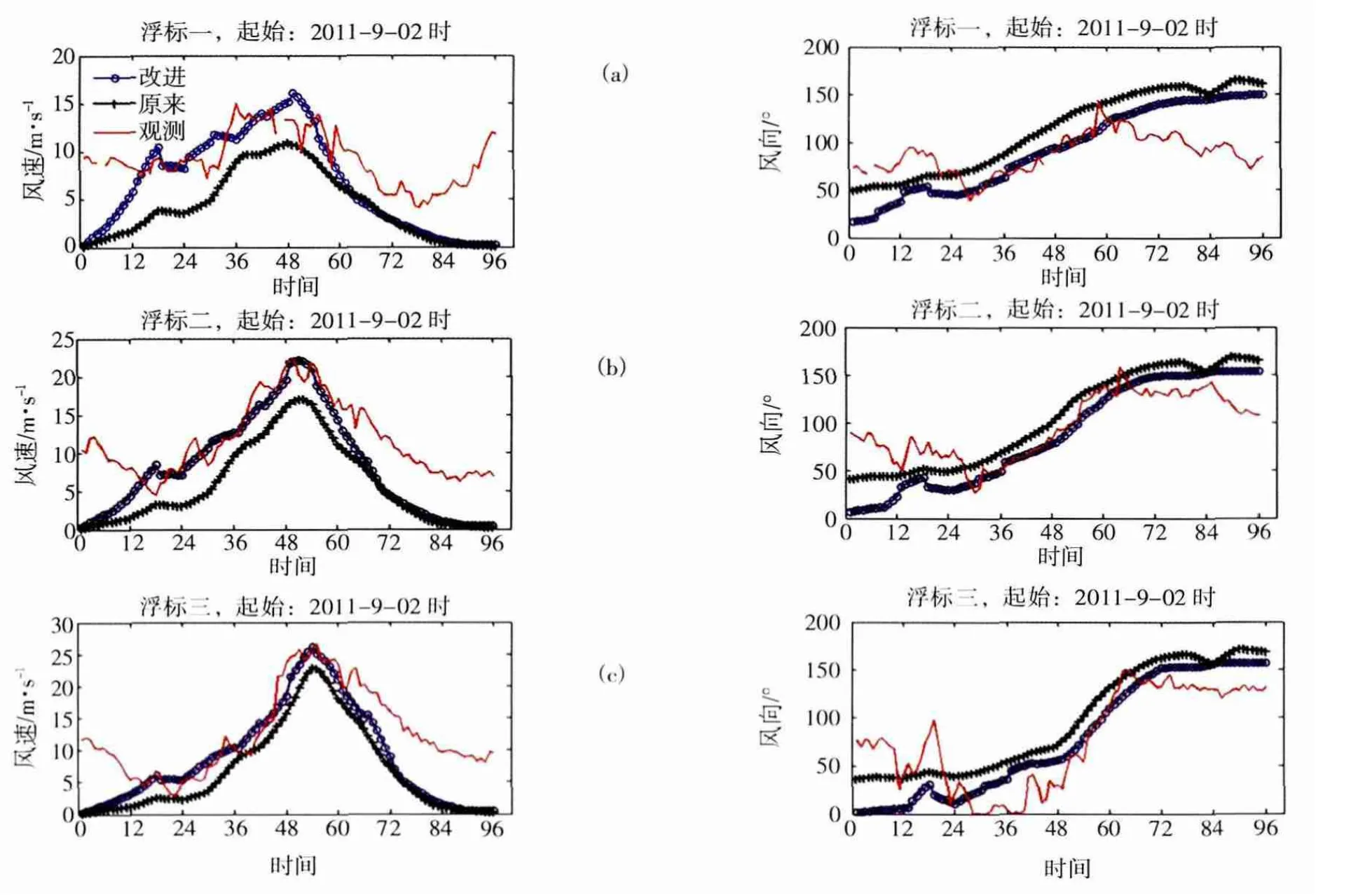
图5 近海浮标一（a）、浮标二（b）、浮标三（c）的风速风向两个模型计算值与实测值比较（原Holland风场-黑色，四象限风场-蓝色，实测-红色）

究其原因：Holland模型在台风实况已知的情况下只能通过改变来调整风圈大小，容易造成热带气旋各象限风场的顾此失彼，而四象限模型可调整风场参数较多，因而四象限模型能够比Holland模型更好地刻画“纳沙”台风风场的非对称性。

4 结论

（1）本文介绍了Holland模型风场和四象限非对称模型风场的求解思路，并分析了两者所构造风场的差异和适用性。

图6 29日14时和29日18时两种模型构造的风场、风暴潮差值

（2）利用ADCIRC模型建立了适合华南沿海的高分辨率风暴潮模式，将上述两种模型风场作为强迫场模拟1117号强台风“纳沙”风暴潮过程，证明该模型是可信的。

（3）通过风暴潮模拟结果可知：在雷州半岛东岸沿海潮位站模拟最大增水平均相对误差基本一致的情况下，珠江口到粤西沿海、琼州海峡附近沿海潮位站模拟最大增水平均相对误差由23.3%降低到5.4%，能够全面地刻画整个受影响岸段的风暴潮发生发展情况。究其原因：四象限模型相比Holland模型更灵活、能够更好刻画“纳沙”台风非对称风场。

Holland G J，1980.An analytic model of the wind and pressure profiles in hurricanes.Mon Wea Rev，108：1212-1218.

Mueller K J， DeMaria M， Knaff J， 2006.Objective Estimation of Tropical Cyclone Wind Structure from Infrared Satellite Data.Weather And Forecasting，21：990-1005.

Westerink，Joannes J，Coauthors，2008：A basin to channel scale unstructured grid hurricane storm surge model applied to Southern Louisiana.Mon Wea Rev，136：833-863.

Xie L，Bao S W，Leonard J，2006.A real-time hurricane surface wind forecasting model： formulation and verification.Mon Wea Rev，134，1355-1370.

陈孔沫，1994.一种计算台风风场的方法，热带海洋，13（2）：41-48.

朱首贤，沙文钰，丁平兴，等，2002.近岸非对称台风场模型.华东师范大学学报（自然科学版），3：66-71.