南京市暴雨地表产流模型研究
2013-08-13陈扬
陈 扬
(南京交通职业技术学院建筑工程系,江苏南京211188)
20世纪80年代以来,中国城市化从起始阶段向加速阶段转变。随着城市化的发展,树木、农作物、草地等面积逐步减小,工业区、商业区和居民区规模、面积不断增大。城市化过程使相当部分的流域为不透水表面所覆盖,减少了蓄水洼地。由于不透水地表的入渗量几乎为零,使径流总量增大;不透水地表的高径流系数使得雨水汇流速度提高,从而使洪峰出现时间提前[1]。这使得城市区域比城郊或乡村地区更容易受到洪涝灾害的侵扰。
为了解暴雨过程中城市地表产汇流过程和机理,进行了本项研究。目前,对于城市地表产流过程,一般采用经典的水文学方法或通过由实验数据拟合成经验公式进行计算的方法进行研究。水文学中的产流模型一般有蓄满产流、超渗产流和蓄满超渗产流等。但这些方法的精度有待提高。本文选择适当的暴雨时程分析方法,依据恰当的暴雨扣损方法,试图建立新的城市地表产流模型,得到城市地表净雨过程线。
1 城市地表产流模型
城市流域的产流过程也就是暴雨扣损过程。当降雨量满足截留和填洼且雨强超过下渗强度时,地面开始积水,并形成地表径流。影响降雨损失过程的因素很多,情况比较复杂,目前在估算或选定损失参数时,主要采用经验方法。城市流域的径流损失主要包括植物截留、洼地填蓄、下渗、蒸发等部分。由于一次降雨中的蒸发损失不大,故一般不单独考虑。
目前,我国的城市暴雨公式的一般形式为:
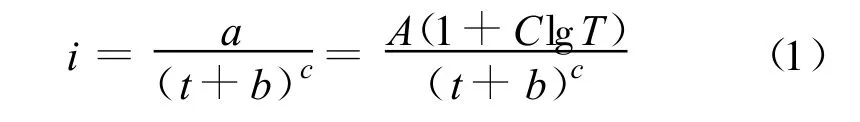
式中:i为降雨强度,a=A(1+1gT);T为重现期;t为降雨历时 ;A、C 、b、c为参数。
从式(1)可以看出,降雨过程中雨强的最大值发生在降雨的初始时刻,显然暴雨公式对于降雨的时程分配模拟得并不符合实际情况[2],所以,需要利用比较恰当的雨型对暴雨公式做比较符合实际的时程分配。本文采用Keifer和Chu雨型。其基本公式为:
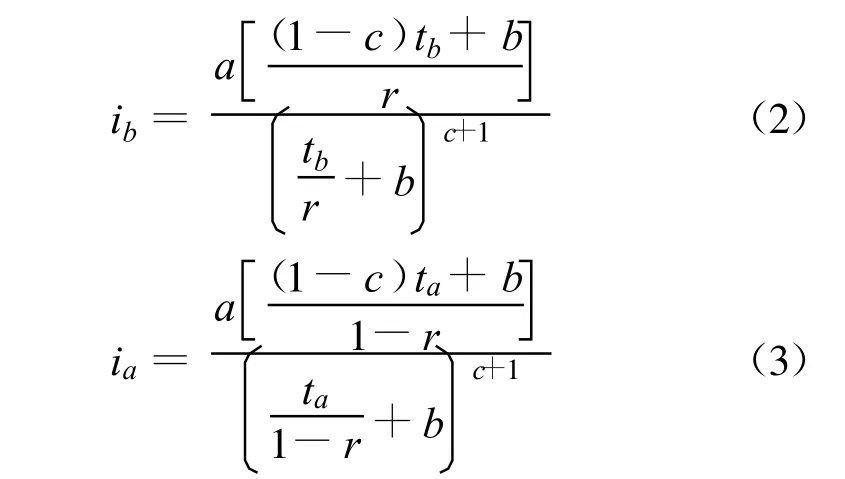
式中:a、b、c与式(1)中意义相同;r为雨峰出现时刻;ib为峰前雨强;ia为峰后雨强;tb为峰前降雨历时;ta为峰后降雨历时。
为了避免时段取得过大,影响转换后瞬时雨量过程线的精度,在编写程序时,取1秒为时段进行计算。同时,为了做进一步研究,引入了两个假设:①由于城市小区的面积较小,所以假设降雨是空间均匀的,即不考虑降雨的空间变化;②假设降雨是时段均匀的,例如取5 min为一个时段,假设降雨强度在每个5 min内相同,而在各个5 min之间不同。对于假设②,具体的处理方法是将瞬时雨量过程线(以1秒为时段)以5 min为时段进行分割,取各5 min时段瞬时雨强的平均值作为5 min时段的雨强。
2 产流计算
岑国平等人在对城市地面产流过程进行系统研究并经过实验验证的基础上,发现不透水面积比例与位置对城市地表产流过程的影响很大。所以在其提出的城市暴雨径流计算模型中,将城市汇流小区分为三类:透水区、直接不透水区和间接不透水区。在本文建立的城市地表产流模型中,借鉴岑国平的分类方法,将城市地表分为三类:不透水区、透水区和混合区。其中混合区指不透水区位于透水区上游的小区域,将它们合在一起叫做混合区。
2.1 不透水区产流计算
本文采用Linsley公式并结合径流系数 ψe通过分步递推的方法来计算城市地表不透水区的产流过程。
不透水区的降雨损失主要有洼蓄、植物截留、缝隙下渗等[3]。本文采用林斯利公式进行不透水区的产流计算。其中洼蓄量 Vd(包括植物截留)按指数曲线逐渐满足,缝隙下渗等损失用径流系数 ψe表示。林斯利公式为:
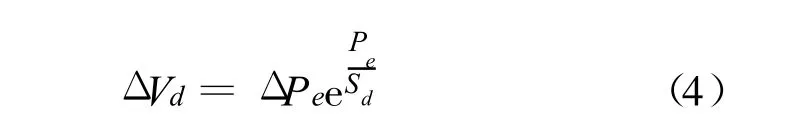
式中:Sd为流域最大洼蓄量(mm);Pe为降雨扣除缝隙下渗的量(mm)。
考虑到实际降雨过程中满足一定基本初损后才有径流出现,经有关研究,将洼蓄总量的1/3作为初损值是比较合理的。因此上式变为:

其中洼蓄总量根据地表坡度、平整程度等确定,一般取2 mm~5 mm。
各时段的洼地蓄水增量为:
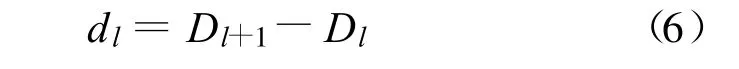
产流开始后各时段的地表净雨深为:

2.2 透水区产流计算
透水区的降雨损失有洼蓄、植物截留和下渗等。其中洼蓄(包括植物截留)的计算方法与不透水区相同,但洼蓄量比不透水区大,一般取3 mm~10 mm。仍取透水区最大洼蓄量的1/3作为基本初损,但与不透水区产流起始时间计算不同的是,透水区的下渗能力较强,需要一段时间的降雨来先满足初始下渗损失,再满足初损,然后按指数形式满足洼蓄且按霍顿公式满足下渗。所以,其产流开始时间由下式计算:
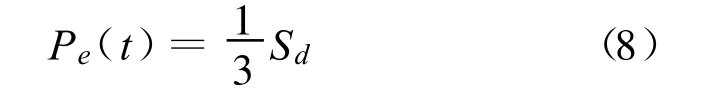
式中:Pe表示降雨扣除下渗损失的量。
下渗采用霍顿公式计算,霍顿公式为:

式中:f为入渗率;fc为稳定入渗率;f0为初始入渗率;t为时间(min);k为与土壤特性有关的经验系数。
产流开始后第i+1时段的洼地蓄水量与不透水区洼蓄计算公式类似。
由此可得,透水区产流开始后第 i时段的净雨为:
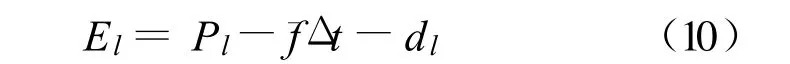
2.3 混合区产流计算
对于混合区来说,不透水面积首先产流,并流入透水面积,使透水面积的产流提前。因此,考虑将混合区中上游不透水区的产流作为输入,使之与下游透水区的雨强叠加,再用透水区的扣损方法进行透水区的产流计算,最后得到整个混合区的产流(见图1)。
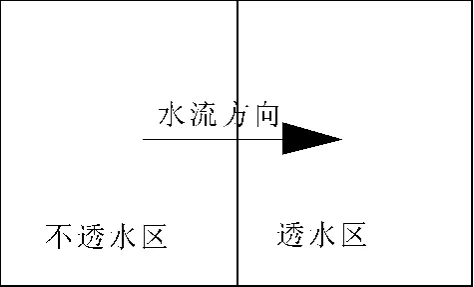
图1 混合区形式
设T为降雨历时,则透水区雨强与不透水区产流的叠加可表示为:
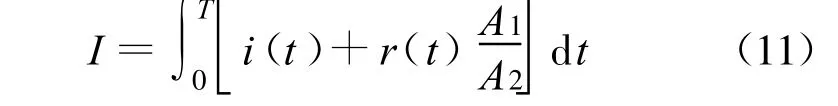
3 计算实例
南京市的暴雨公式为[4]:

转换成用雨强表示的形式为:
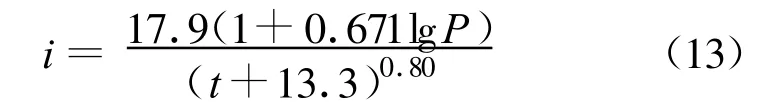
取3年重现期的120 min历时降雨[5],雨峰位置在0.4倍降雨历时处来计算,时间步长为5 min。
3.1 不透水区计算实例
取不透水区最大洼蓄量为3 mm,最终径流系数为0.85[6],进行计算。得到产流开始时间和产流过程线如图2。
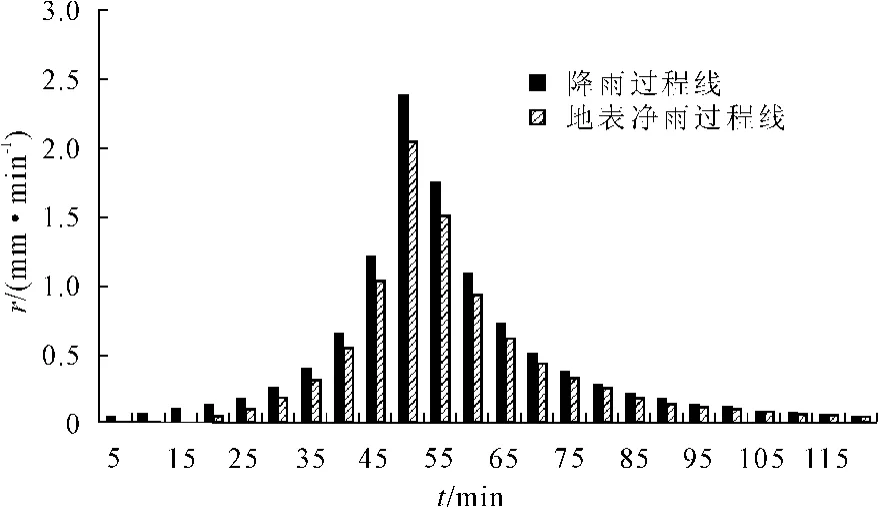
图2 不透水区各时段地表净雨图
3.2 透水区的计算实例
参照城市区域典型地面洼蓄深和城市区域内Horton方程中的下渗参数参考值[7],取透水区最小初始下渗率为1.25 mm/min,最小稳定下渗率为10 mm/min最大初始下渗率为3.5 mm/min,最大稳定下渗率为0.30 mm/min;k为0.0350 min;最大洼蓄量为5mm。得到产流开始时间和产流过程线如图3。
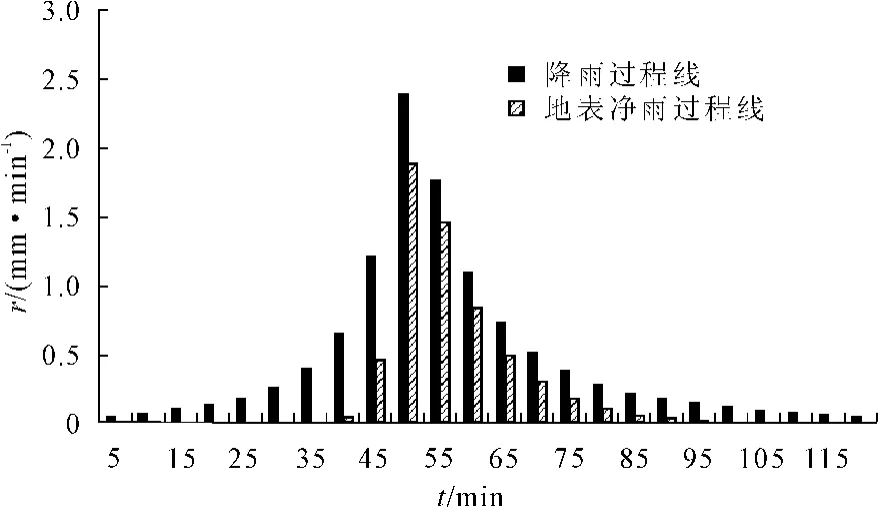
图3 透水区各时段地表净雨图
3.3 混合区的计算实例
取混合区中的不透水部分和透水部分与上述不透水区和透水区流域特性相同,不透水部分占40%,透水部分占60%。得到产流开始时间和产流过程线如图4。

图4 混合区各时段地表净雨图
4 结 论
本文基于城市水文学和水力学原理,并参考了国内外的一些城市暴雨径流模型,将城市区域划分为不透水区域、透水区域和混合区域等小流域,在霍顿下渗公式和林斯利公式的基础上,考虑截留、填洼、下渗等损失,建立了相应的城市地表产流模型,同时根据产流模型编制了相关程序。最后利用南京市的暴雨条件对模型进行了验证,计算出地表净雨产流过程线。从结果可以看出,城市地表的净雨最大值发生在0.3 T~0.5 T之间,不透水区的净雨强度大于混合区的净雨强度,混合区的净雨强度大于透水区的净雨强度,这和城市实测的降雨资料是吻合的。
[1]王建鹏,薛春芳,解以扬,等.基于内涝模型的西安市区强降水内涝成因分析[J].气象科技,2008,36(6):772-775.
[2]徐向阳,刘 俊,郝庆庆,等.城市暴雨积水过程的模拟[J].水科学进展,2003,14(2):193-196.
[3]解以扬,李大鸣,李培彦,等.城市暴雨内涝数学模型的研究与应用[J].水科学进展,2005,16(3):384-390.
[4]孙慧修.排水工程(第四版)[M].北京:中国建筑工业出版社,1999.
[5]刘金星.城市暴雨径流模型及透水式管道设计方法研究[D].杭州:浙江大学,2005:25-28.
[6]解以扬,李大鸣,沈树勤,等.“030704”南京市特大暴雨内涝灾害的仿真模拟[J].长江科学院院报,2004,21(6):73-76.
[7]张配亮.天津市区暴雨径流模拟模型的研究[D].天津:天津大学,2007:53-55.
