小波变换和形态学相结合的图像融合新算法
2013-08-13杨卫英丁友东
罗 婷,杨卫英,丁友东
(上海大学影视艺术技术学院,上海 200072)
图像融合是通过综合各种图像数据的优势,来提升图像的解译能力[1]。传统的图像融合算法没有考虑到融合图像的边缘信息,容易出现边缘模糊导致融合图像清晰度降低的问题,因此边缘信息对于融合质量有很大影响。针对这一问题,本文提出了将小波变换同数学形态学相结合的图像融合新算法,该算法同时结合了小波变换法和数学形态学的优点。图像的小波变换具有多分辨率、方向性好、无冗余、在频域和时域上同时具备良好的局部性、可以“聚焦”到图像的任意细节处等特性。数学形态学不仅能简化图像,还能在保持基本形状的基础上除去不相干结构[2]。数学形态学的边缘检测方法比其它的空域或频域的图像边缘检测方法具有明显的优势[3],其检测提取到的边缘更加光滑、完整和连续。因此,将小波变换同数学形态学相结合应用于对多聚焦模糊图像之间或者降质退化图像之间的融合具有明显的优势,融合后图像边缘轮廓及细节更清晰,融合质量进一步提高。
文献[4]提出了一种基于形态学小波的图像融合算法,融合质量得到了一定的提升,但融合后图像边缘轮廓细节处出现降质退化虚化现象。而用本文算法融合后,融合质量得到了进一步的提升,边缘轮廓及细节更清晰,效果更好。
1 小波变换和形态学结合图像融合新算法
本文算法流程如下:
1)对每一幅原始图像分别进行小波分解,分离出高频信息和低频信息。
2)对每个小波分解层上的高频信息和低频信息分别采用如下不同的融合规则进行融合。
3)对融合后得到的小波系数进行小波逆变换重构图像。
若对二维图像进行N层的小波分解,最终将有3N+1个不同频带,其中包含3 N个高频带和1个低频带[5]。设A和B为两幅原始图像,F为融合后图像,基于小波变换的图像融合原理如图1所示。
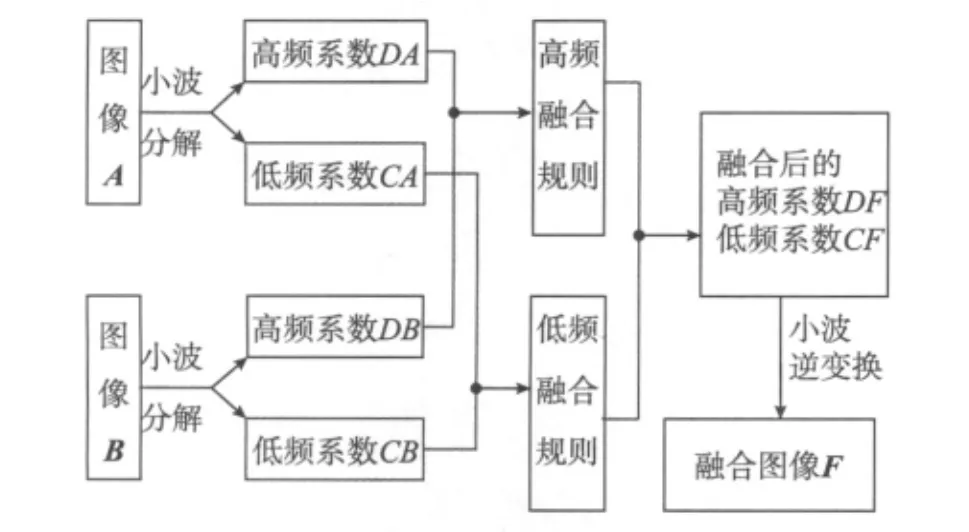
图1 基于小波变换的图像融合原理
对于高频信息和低频信息,各自的融合规则如下文所述。
1.1 高频融合规则
高频信息代表了图像的细节信息,选取绝对值较大的高频系数能更好地保留原始图像的边缘等特征。因此,本文选用绝对值取大法来融合高频系数,为了能进一步增强图像边缘细节等特征,对得到的高频系数再进行适当的增大。高频系数的融合过程如图2所示。
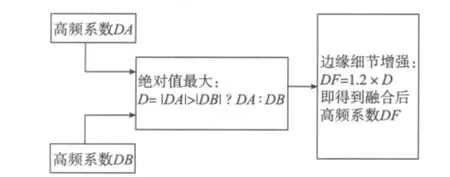
图2 高频系数的融合过程
1.2 低频融合规则
目前不少基于小波法的图像融合算法只单单选用平均法进行低频系数的融合,会降低图像的对比度,引起目标或场景的不清晰。低频系数决定着图像的轮廓,因而正确选择低频系数对提升最后的图像融合质量具有举足轻重的作用[6]。
对原始图像A和B进行小波分解后,得到低频子图像LA和LB。针对LA,区域块大小是2×2,假设P点位置是(i,j),则点 P 的区域块包含了P(i,j),P(i,j+1),P(i+1,j),P(i+1,j+1),计算点P区域块内的空间频率为该点P处的区域空间频率。同理,针对LB,操作方法和LA相同。
然后,运用数学形态学方法对LA和LB进行边缘检测,为了能够更精细且更快速地提取边缘,结构元素选用3×3的结构平面,采用形态学膨胀运算进行边缘检测,灰度膨胀边缘检测算子运算式为

式中:EA,EB表示边缘灰度图像;B表示结构元素。得到了边缘灰度图像EA和EB,之后遍历EA和EB的每一像素点的位置,如果该点像素值≥153,则该点记作边缘点,反之记作非边缘点(选153作分界点,因为灰度图像的像素值在0~255之间,像素值为0代表黑色,像素值为255代表白色,而边缘点的特征是灰度值比较大,因此分界点不能太小,至少要大于中间值128,否则很有可能会把那些非边缘点误认为边缘点,另外如果分界点过大,可能出现边缘点被误认为是非边缘点的情况,导致很多边缘点可能会被遗漏,因此分界点不能过大,也不能小于中间值128,再进一步通过多组实验后得出以153作为分界点比较合适且合理)。
当在EA和EB上相同位置处的点EA(i,j)和EB(i,j)都是非边缘点时,选用平均法融合此点位置处对应的低频系数;反之,比较之前已经计算好的像素点LA(i,j)和LB(i,j)的区域空间频率值SFA和SFB,选择区域空间频率较大的此像素点位置处所对应的低频系数作为融合后的低频系数。这是因为如果点LA(i,j)处的轮廓边缘比较模糊虚化,则此点的区域空间频率就会比较小,而如果点LB(i,j)处的轮廓边缘相对比较清晰分明,则该点的区域空间频率就会比较大,就可以用该点LB(i,j)处对应的低频系数作为融合后的低频系数,这样融合后的低频边缘信息的清晰度得到了一定的提高。
低频系数的融合过程如图3所示。
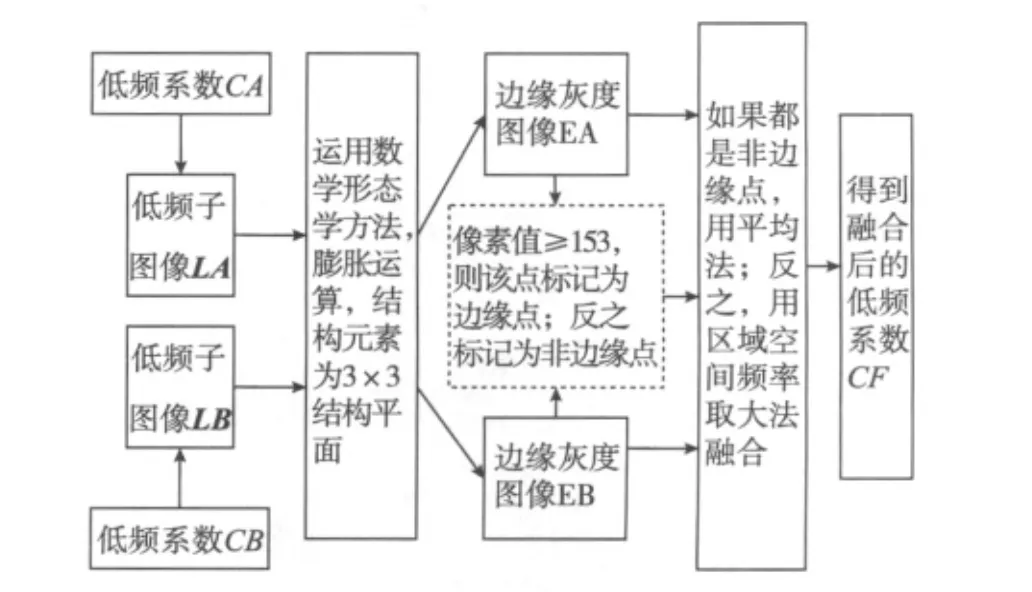
图3 低频系数的融合过程
2 实验结果与评价
2.1 图像融合评价标准
本文采用5种指标来评价图像融合效果的优劣。
1)灰度均值:反映了这幅图像的平均亮度。
2)标准差:反映了灰度值相对于图像灰度均值的离散程度。如果标准差越大,那么灰度级分布就越分散,图像的明暗对比度越大,可获得的信息就越多,图像融合效果也就越好。
3)平均梯度:用于评价图像清晰度,反映图像中纹理变换特征和微小细节反差[6]。平均梯度值越高,图像包含的细节越丰富,图像越清晰,融合效果也就越好。
4)互信息[7]:衡量融合图像从原始图像中继承信息量的多少。其值越大,融合效果就越好。
5)信息熵:代表了一幅图像含有信息的丰富程度[8]。信息熵越大,图像包含的平均信息量越多,融合效果也就越好。
2.2 实验结果与分析
为了验证本文算法的可行性和有效性,先后对2组图像进行实验。所选用的2组实验图例都是没有同时聚焦或者因降质退化而变得模糊不清。
第1组实验选用了2幅标准图像,如图4a、图4b所示。不同融合算法的效果图对比如图4c~图4i所示。不同融合算法的效果图细节处的对比如图5所示。从图5a,5c,5d,5f中可看出,像素值选大法、加权平均法、形态学算法和文献[4]算法得到的融合效果的细节处的数字10和11出现了不同程度的虚化模糊,降质退化现象明显。从图4和图5可看出,用本文算法融合后的效果图的对比度更大,颜色明暗层次更分明、更清晰化,视觉效果更好。融合算法的评价比较如表1所示,可看出,用本文算法融合后,平均梯度都远远高于其余6种融合算法,标准差、信息熵值也都达到了最大值,虽然互信息值不是最高,但是综合的质量评价指标还是最优的。因此,无论从效果图的主观评价,还是从客观评价标准指标参数分析,本文算法融合质量更优。

图4 不同融合算法的效果图对比

图5 不同融合算法的效果图细节处对比
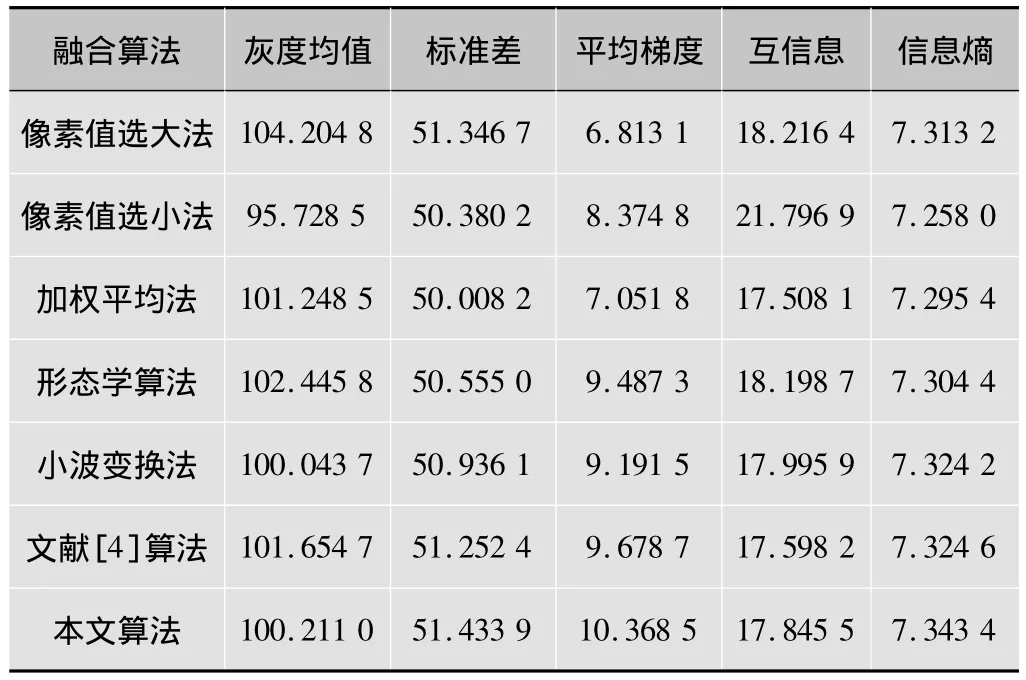
表1 不同融合算法的评价比较
第2组实验选用了2幅标准图像,如图6a,6b所示。不同融合算法效果图对比如图6c~图6i所示。不同融合算法的效果图细节处的对比如图7所示。从图7a,7c,7d,7f可看出,像素值选大法、加权平均法、形态学算法和文献[4]算法得到的融合效果图的细节处的英文和数字不清晰,降质退化现象比较严重。从图7b可看出像素值选小法融合结果细节处的英文出现了很明显的叠影。从图6和图7可看出,用本文算法融合后的结果图对比度更强,图像细节处更清晰,融合效果更好。融合算法的评价比较如表2所示,可看出,用本文算法融合后,平均梯度值和互信息都远远高于其余6种融合算法,信息熵值也达到最大,标准差也相对很大,整体综合的融合质量评价指标是最优的,因此,本文算法的融合质量更好。
3 结论


本文提出了将小波变换和数学形态学相结合的图像融合新算法。将多幅图像进行小波分解后,在融合高频系数的过程中,选用绝对值取大法,并适当增强了高频图像边缘细节。在融合低频系数的过程中,运用到了数学形态学方法对低频子图像进行边缘检测,并得到边缘灰度图像,在边缘灰度图像中,按照该点的像素值是否≥153,来标记该点是否为边缘点,之后针对该位置的点是否是边缘点,分别用区域空间频率取大法和平均法融合该点位置处对应的低频系数。通过将本文算法和传统的图像融合算法及文献[4]算法进行2组实验的效果图对比,并同时结合了5种质量评价指标比较分析,实验结果表明,本文算法的融合质量更好,图像边缘轮廓及细节更清晰,图像融合质量得到了进一步的提升,该算法是有效、可行的。
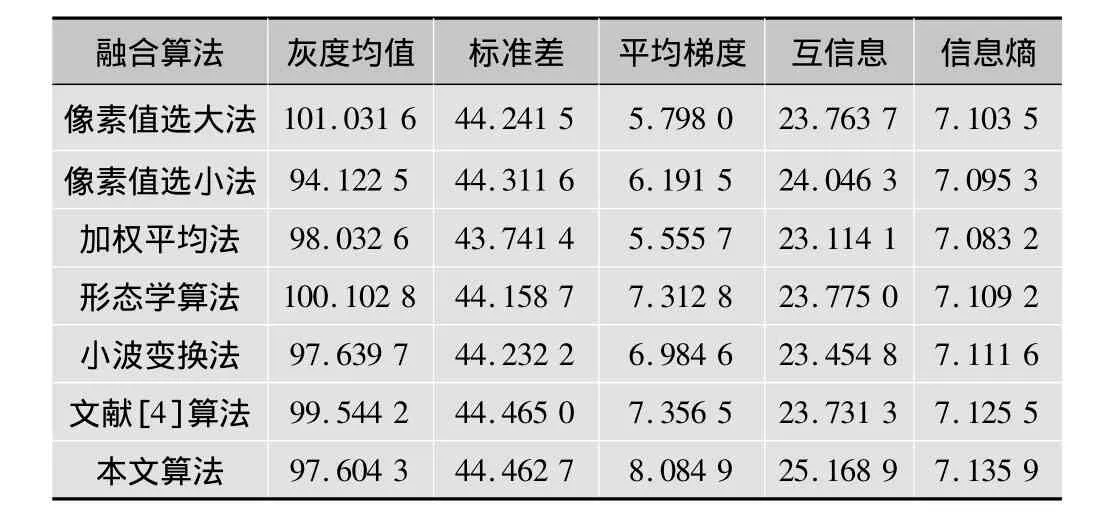
表2 融合算法的评价比较
[1]PIELLA G.A general framework for multi-resolution image fusion:from pixels to regions[J].Information Fusion,2003,68(4):259-280.
[2]王树文,闫成新,张天序,等.数学形态学在图像处理中的应用[J].计算机工程与应用,2004,32(89):89-92.
[3]陈琳.基于数学形态学的图像分割技术研究[D].昆明:昆明理工大学,2006.
[4]钱永浩,吴小俊,罗晓清.改进的基于形态学小波多聚焦图像融合方法[J].计算机工程与应用,2010,46(7):158-161.
[5]曾基兵,陈怀新,王卫星.基于改进局部梯度的小波图像融合方法[J].电视技术,2007,31(8):18-20.
[6]於时才,吕艳琼.一种基于小波变换的图像融合新算法[J].计算机应用研究,2009,26(1):390-391.
[7]范文涛.基于小波变换的图像融合技术研究[D].郑州:河南大学,2010.
[8]浦西龙.基于多分辨小波的像素级图像融合研究[D].苏州:苏州大学,2007.
