通用数字图像加密与抗剪切攻击恢复算法

卢守东

(广西财经学院信息与统计学院，广西 南宁 530003)

图像具有生动形象的特点，应用十分广泛。经过数字化而成的数字图像可由计算机高效处理，并能在网络中快速传播。为对数字图像进行有效的保护，可采用相应的加密技术。数字图像加密是目前数字图像处理领域的一个重要研究方向［1-3］，基于各种混沌系统的数字图像加密算法也已成为近年来的研究热点之一，诸多各具特点、切实可行的算法已相继出现在有关的文献中［4-8］。

通过对图像加密技术及有关算法的研究，本文以混沌系统及其产生的混沌序列为基础，提出一种通用的综合使用像素坐标置乱与像素值置换技术的数字图像加密与解密算法，同时给出一种基于邻域相邻像素特性的抗剪切攻击恢复算法。

1 混沌序列

混沌序列是混沌系统中所出现的混沌现象的运动轨迹。根据混沌系统的方程，指定不同的参数与初值，即可产生一系列非相关、类随机、确定可再生的混沌序列。混沌序列对系统的参数与初值极其敏感，且在一定的区域内具有遍历性与伪随机性，因此可用于对数字图像进行加密，而相应的系统参数与初值均可作为密钥的组成部分。

Logistic映射是目前应用得相当广泛的、典型的一维混沌系统，定义为［4］

式中:μ 为分支参数，且 μ∈［0，4］，xn∈(0，1)，n=0，1，2，…。研究表明，当3.5699456＜μ≤4时，Logistic映射所生成的混沌序列{xn，n=0，1，2，3，…}具有良好的随机分布特性与遍历性，是一种比较理想的伪随机序列，且对初值x0十分敏感。在应用Logistic映射时，μ与x0均可作为密钥使用。

Logistic映射具有良好的“雪崩效应”。为提高安全性，在使用 Logistic 混沌序列{xn，n=0，1，2，3，…}时，可适当舍弃其前面的N个数据项(一般取N≥20)。相应地，N也可作为密钥的组成部分之一。

本文在进行仿真实验时，用于生成Logistic混沌序列的密钥 key=(μ，x0，N)。

2 基于混沌序列的像素坐标置乱

像素坐标置乱是指对图像的像素坐标进行变换以使其混乱。考虑到混沌序列的固有特性，可由混沌序列决定像素坐标的变换位置，以达到理想的置乱效果。

假定图像的大小为m×n，由密钥key=(μ，x0，N)产生具有相应长度的混沌序列{x1，x2，x3，…，xm×n}，将其按升序或降序进行排序得到有序序列{xindex(1)，xindex(2)，xindex(3)，…，xindex(m×n)}，则该有序序列各数据项的下标序列{index(1)，index(2)，index(3)，…，index(m × n)}即为整数序列{1，2，3，…，m×n}的一个排列。据此，可构造一个1-1变换Φ:k→index(k)。利用此变换Φ，可将该图像的像素(i，j)(其中 i=0，1，2，…，m-1;j=0，1，2，…，n-1)按行列顺序变换到新位置(row，col)

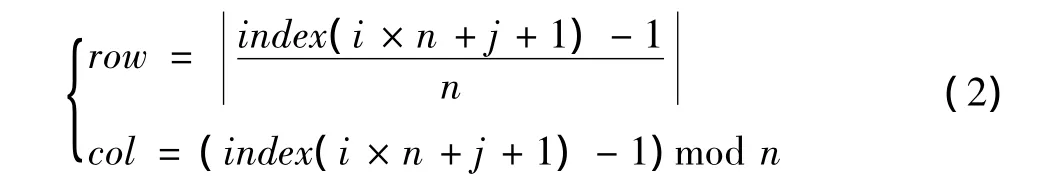
经过像素的坐标变换后，图像将变得面目全非。

3 基于混沌序列的像素值置换

像素值置换是指对图像的像素值进行变换以改变其值。考虑到混沌序列的良好特性，可由混沌序列生成相应的操作数，然后再与各像素值分别进行异或运算，从而达到理想的置换效果。

假定图像的大小为m×n，由密钥key=(μ，x0，N)产生具有相应长度的混沌序列{x1，x2，x3，…，xm×n}，将其按图像类型转换为无符号整数序列{z1，z2，z3，…，zm×n}，然后与该图像的像素值P(i，j)分别进行异或运算，即可得到置换后的像素值Pe(i，j)。

混沌序列转换为无符号整数序列的公式为

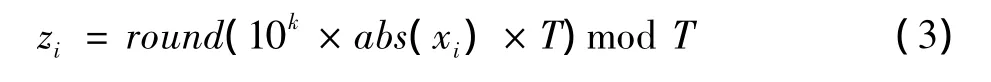
式中:i=1，2，3，…，m ×n;k=0，1，2，3，…;abs表示取绝对值;round表示取最近整数;T=2h为图像类型值，h为二值图像、灰度图像或RGB真彩图像各分量的比特深度。据此，可将k作为子密钥使用。

像素值置换的公式为

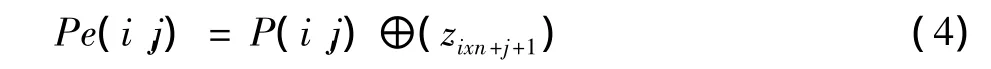
式中:i=0，1，2，…，m-1;j=0，1，2，…，n-1。

反之，像素值恢复的公式为

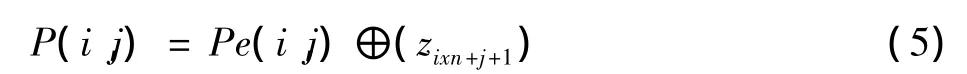
经过图像像素值的随机置换后，原图像的灰度直方图统计特性将被彻底改变。

4 加密与解密算法

在进行数字图像的加密时，同时采用基于混沌序列的像素坐标置乱与像素值置换，可有效提高加密图像的抗剪切攻击能力和抗像素特征值统计攻击能力。若在进行像素坐标置乱与像素值置换时使用的不同的混沌序列，则加密效果更佳。

为简单起见，本文加密算法基于同样的一个混沌序列进行像素坐标置乱与像素值置换，其主要步骤为:

1)读取待加密图像，生成像素矩阵P，并确定其大小m×n与图像类型值T。

2)由密钥key=(μ，x0，N)产生一个长度为m×n的混沌序列{x1，x2，x3，…，xm×n}。

3)将{x1，x2，x3，…，xm×n}按升序或降序进行排序，得到有序序列{xindex(1)，xindex(2)，xindex(3)，…，xindex(m×n)}，并据此生成下标序列{index(1)，index(2)，index(3)，…，index(m ×n)}。

4)根据{index(1)，index(2)，index(3)，…，index(m ×n)}及变换Φ:k→index(k)，将像素坐标(i，j)按行列顺序变换到新位置(row，col)，生成像素坐标置乱后的图像加密矩阵PE。

5)根据子密钥 k及图像类型值 T，将{x1，x2，x3，…，xm×n}转换为无符号整数序列{z1，z2，z3，…，zm×n}。

6)将{z1，z2，z3，…，zm×n}中的各个数据项分别与像素矩阵PE中的对应的像素值进行异或运算，生成像素值置换后的图像加密矩阵P。

7)由像素矩阵P生成加密图像。

本加密算法是可逆的，因此解密算法与加密算法具有相同的密钥，但应先恢复像素的值，然后再将各像素变换至其原来所在的坐标位置。

5 抗剪切攻击恢复算法

针对恶意剪切等攻击，可采用相应的抗剪切攻击恢复算法(简称为ASAR算法)，进一步提高解密图像的质量。

5.1 剪切区域的检测

像素坐标置乱与像素值置换的双重加密过程，极大地降低了图像相邻像素之间的相关性，加密图像中的像素值已呈随机分布状态，并均匀扩散至整个取值范围。因此，若发现连续的、等值的多个像素，则可认为这些像素是被剪切的。为降低误检率，一般应取3～6个连续像素作为判断条件。

首先，创建一个与加密图像大小一致的剪切区域标记零矩阵CF。然后，逐行扫描加密图像，若发现连续多个(本文算法为6个)像素的值相同，则将CF中与这些像素对应的元素置为255。

对于RGB加密图像，可通过逐一比较CF各分量中对应元素的值，将最终的剪切区域修正为各分量的相交部分。

本剪切区域检测算法采用等值的像素扫描判断技术，因此同样适用于涂鸦、污损等恶意攻击的情形。

5.2 解密图像的恢复

加密图像解密后，被剪切的像素将按加密时的坐标对应关系变换至其原始位置，从而在整个解密图像中呈均匀分布状态。根据4邻域相邻像素的高度相关特性，可将邻域像素的平均值作为各被剪切像素的值。本文解密图像恢复算法的基本步骤为:

1)按对加密图像进行解密时各像素的坐标变换关系，将CF中的各个元素变换至相应像素在解密图像中的坐标所对应的位置，得到一个相应的图像恢复标记矩阵RF。

2)置unfinished为0。

3)逐行逐列扫描RF，若某个元素值为255，则计算其4邻域中未被剪切(或已被恢复)的像素的个数n以及相应的像素值之和s。若n≥2，则将该元素的值置为0，同时将对应的像素值置为平均值round(s/n);否则，置unfinished为1。

4)若unfinished=1，则转至2)。

6 实验结果与分析

6.1 实验结果

本文使用MATLAB R2007a平台，对各类常见图像按文中算法进行仿真实验。实验采用同样的一个Logistic混沌序列对图像进行像素坐标置乱与像素值置换加密，密钥 key=(μ，x0，N)=(3.69，0.56789，50)，子密钥 k=3。对于RGB真彩图像，亦采用同样的混沌序列并按同样的方式加密其R，G，B各分量。图像经加密后，均变得杂乱无章、面目全非，证明了算法的有效性。限于篇幅，在此只列出几个有代表性的例子。实验结果见图1～图5。

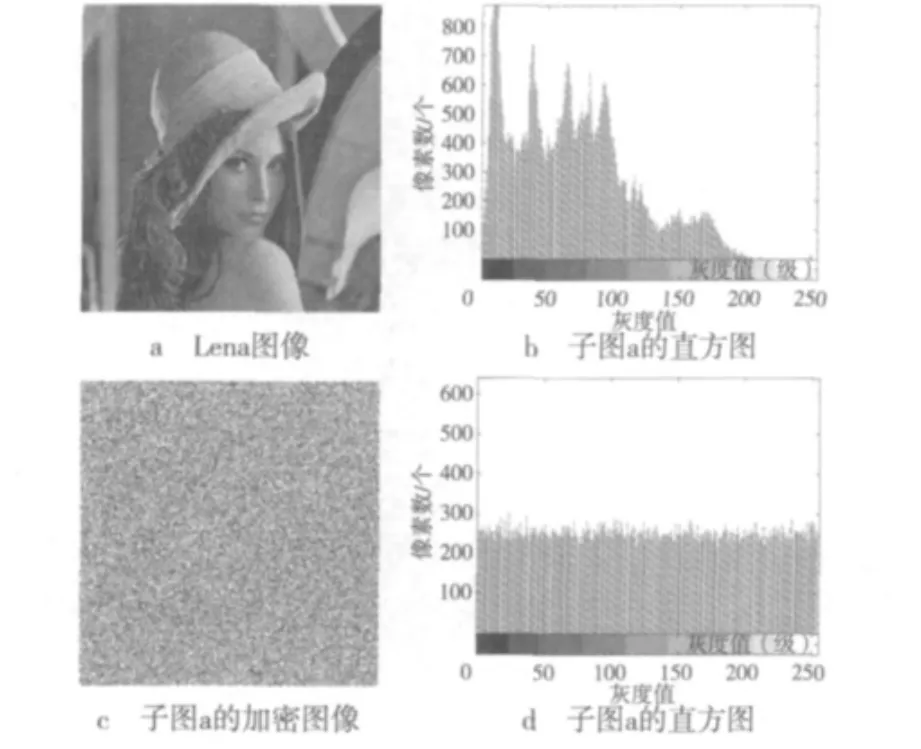
图1 本文算法灰度图像Lena加密效果

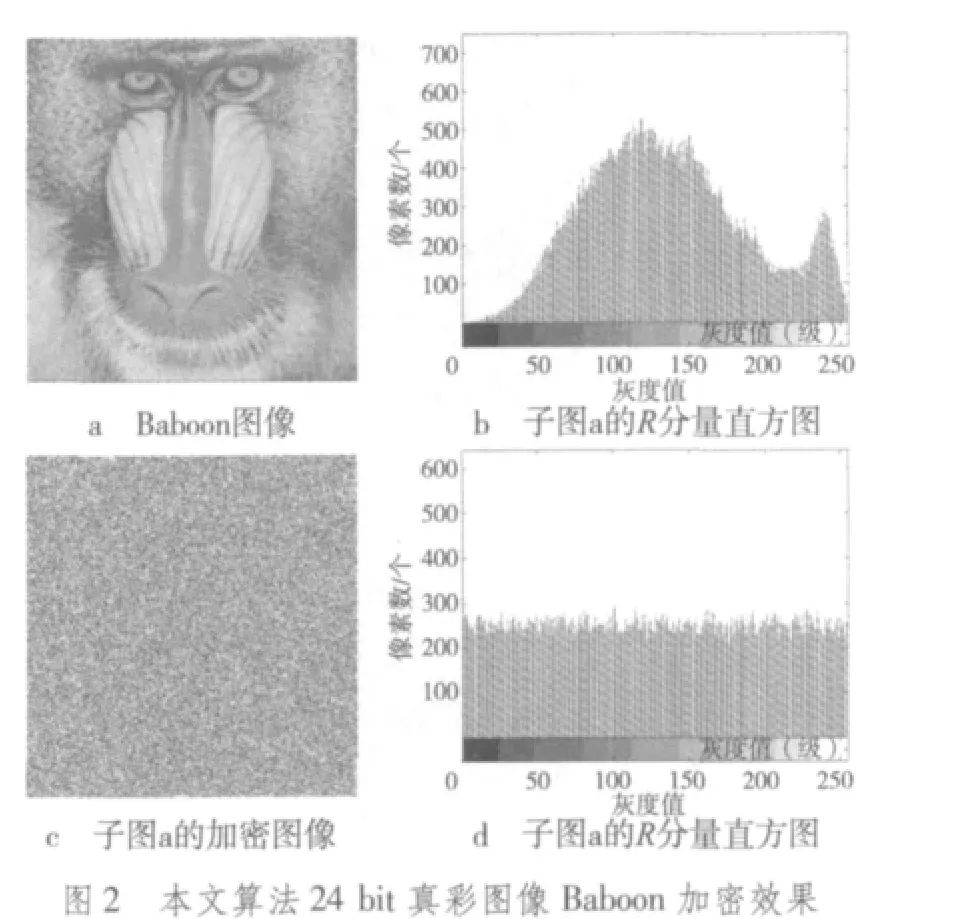
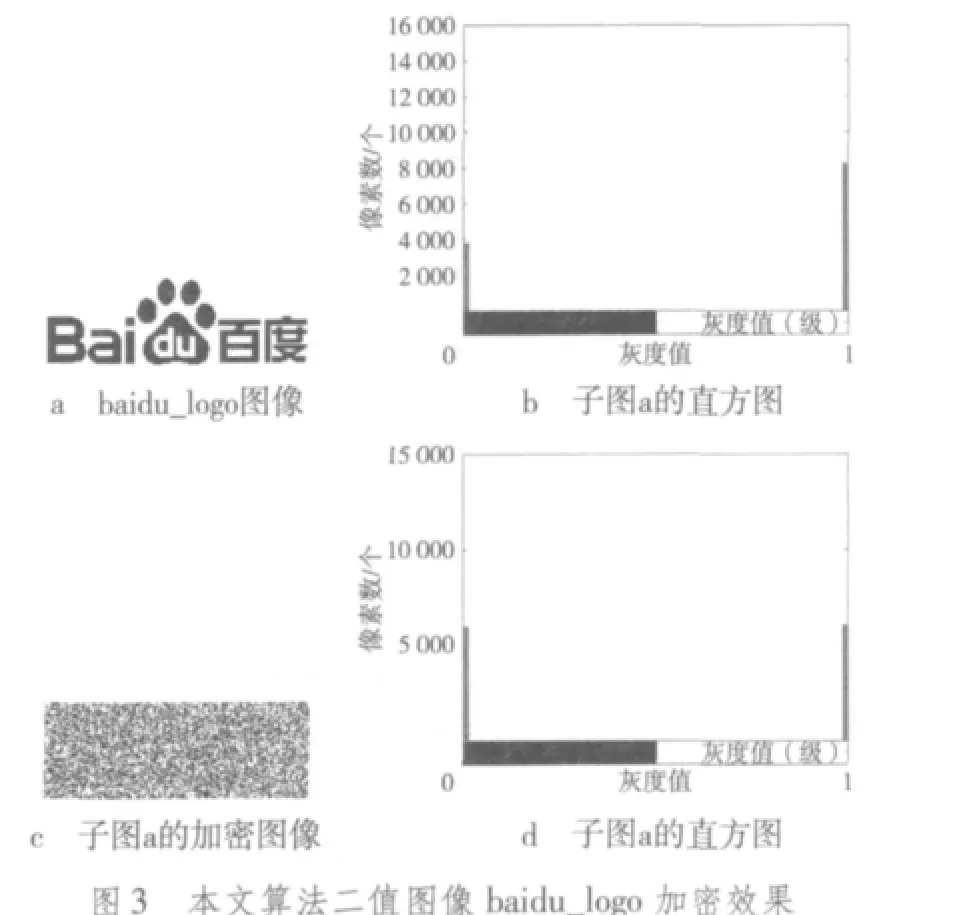
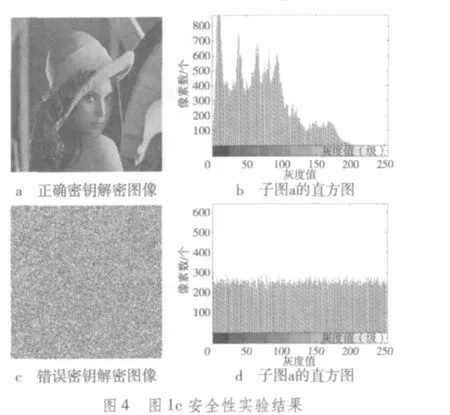
图5 图1c抗剪切攻击实验结果

6.2 安全性分析

如图4所示的安全性实验表明，即使只对初值x0进行微小修改(仅相差10-10)，也将导致解密的完全失败，此时所生成的解密图像依然类似于待解密的加密图像。同样，只对其余的某个密钥分量(μ，N或k)进行微调时，结果亦与此类似。只有在使用完全正确的密钥与子密钥时，才能确保解密成功。可见，本文算法具有极强的密钥敏感性。此外，本文算法的密钥分量较多(包括浮点型的μ，x0的与整型的N，k)，因此拥有颇为巨大的密钥空间，可有效抵御穷举攻击。

6.3 统计特性分析

1)灰度直方图

通过对各类图像在加密前后的灰度直方图进行比较，可以发现其差异是十分明显的。图像经过加密以后，其像素在整个取值范围内的分布相当均匀，表明本文算法具有良好的扩散性，可完全改变图像的像素值统计特性。

2)相邻像素的相关性

图像相邻像素的相关系数用于度量相邻像素的相关性，其计算公式为［5］

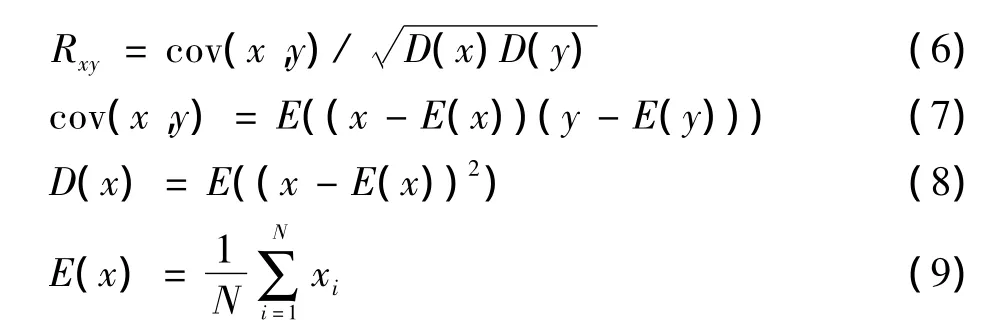
式中:x，y为图像中两个相邻像素的灰度值。

Lena，baidu_logo与Baboon图像在加密前后的相邻像素相关系数分别如表1、表2所示。实验数据表明，原始图像在水平、垂直与对角方向的相邻像素的相关系数均接近于±1.00，说明存在着高度相关性;而加密图像在各个方向的相邻像素的相关系数均接近于0，说明已呈几乎不相关状态。

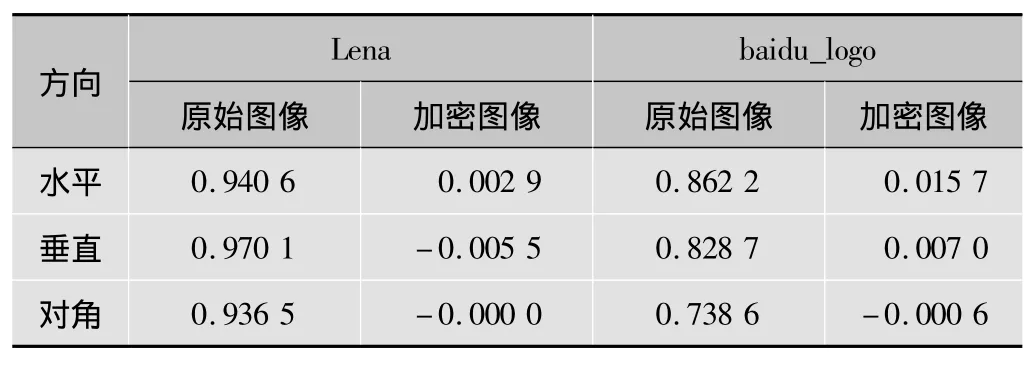
表1 Lena与baidu_logo图像相邻像素的相关系数

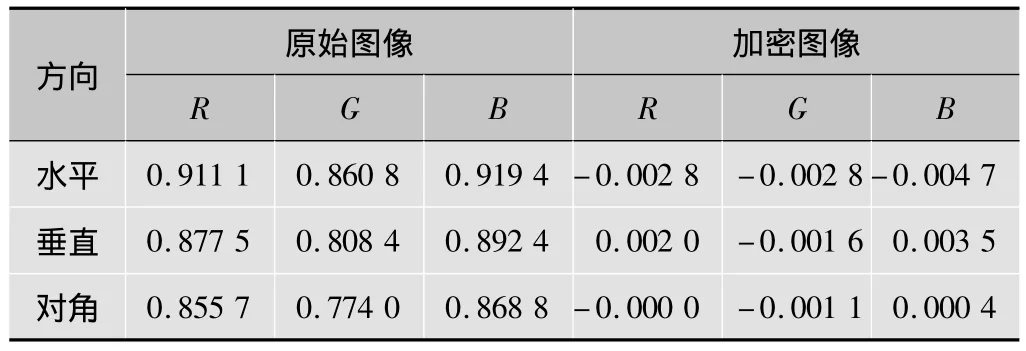
表2 Baboon图像R，G，B分量相邻像素的相关系数

3)信息熵

图像的信息熵用于度量图像中灰度值的均匀分布情况，其计算公式为［6］

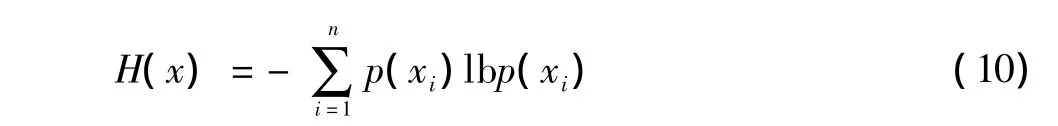
式中:p(xi)为图像像素值xi出现的概率。

Lena，baidu_logo与Baboon图像在加密前后的信息熵分别如表3、表4所示。实验数据表明，Lena加密图像与Baboon加密图像R，G，B各分量的信息熵均接近于8(256级灰度图像信息熵的理论最大值)，baidu_logo加密图像的信息熵则刚好等于1(二值图像信息熵的理论最大值)。可见，经本文算法加密后，图像的像素值分布已相当均匀，且其出现概率亦几乎是一致的。

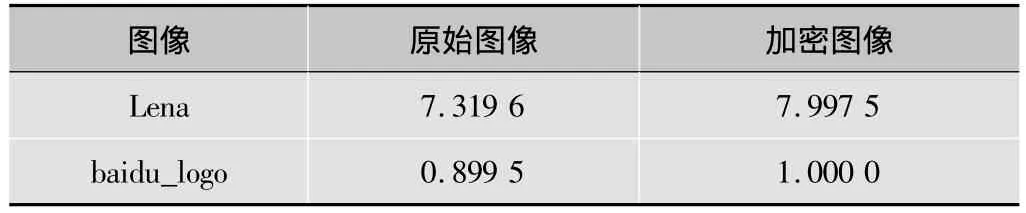
表3 Lena与baidu_logo图像的信息熵

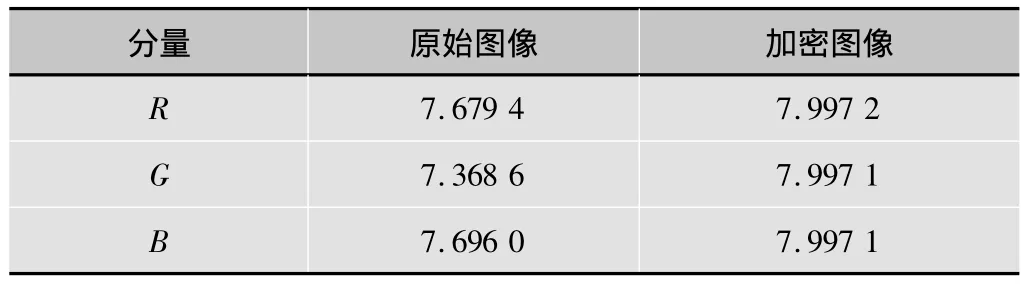
表4 Baboon图像R，G，B分量的信息熵

6.4 抗剪切能力

如图5所示的抗剪切攻击实验表明，即使加密图像被随机剪切的面积达到50%，仍然能够直接解密出相当不错的可识别的图像，进一步应用ASAR算法时则可得到还原质量更佳的恢复图像，可见本文加密算法的抗剪切攻击能力是较强的，而ASAR算法也是有效可行的。从峰值信噪比PSNR看，图5c和图5d分别为16.6685，10.6598，而图5e和图5f分别为25.6262，21.2186，这也客观地表明了本文ASAR算法的有效性。

7 结束语

基于混沌系统及其所产生的混沌序列，本文提出了一种通用的数字图像加密与解密算法，同时给出了一种基于邻域相邻像素特性的抗剪切攻击恢复算法。文中的加密算法充分利用了混沌序列的固有特性，并采用像素坐标置乱与像素值置换相结合的双重加密技术，具有较强的安全性。此外，该算法对于图像的类型及大小没有任何限制，并可使用Logistic，Henon，Lorenz等各类混沌系统所产生的混沌序列，且易于实现，具有良好适应性与实用性。为进一步提高数字图像的加密效果，可对本文算法进行相应的改进，如使用不同的混沌序列进行像素坐标置乱与像素值置换，或同时使用两种不同的混沌系统等。

［1］李昌刚，韩正之，张浩然.图像加密技术综述［J］.计算机研究与发展，2002，39(10):1317-1324.

［2］李昌刚，韩正之.图像加密技术新进展［J］.信息与控制，2003，32(4):339-343.

［3］孙燮华.数字图像处理:原理与算法［M］.北京:机械工业出版社，2010.

［4］高飞，李兴华.基于混沌序列的位图像加密研究［J］.北京理工大学学报，2005，25(5):447-450.

［5］李太勇，贾华丁，吴江.基于三维混沌序列的数字图像加密算法［J］.计算机应用，2006，26(7):1652-1654.

［6］李鹏，田东平.基于超混沌序列的数字图像加密算法［J］.微电子学与计算机，2008，25(3):4-7.

［7］刘刚，王立香.一种新的基于混沌的图像加密算法［J］.电视技术，2008，32(12):22-24.

［8］成亚萍，吕巍，张太忠.一种新的抗剪切的数字图像加密算法［J］.计算机工程与应用，2008，44(27):130-131.