金融时间序列聚类分析方法比较研究——基于上市公司股票收益率的实证分析

赵 冲

（首都经济贸易大学，北京100070）

引言

时间序列聚类在很多领域有重要的作用，如金融和经济，工程学和生命科学等等。时间序列聚类有多种方法，聚类时通常要构建两个时间序列之间的相异度度量。如Piccolo (1990)[14]和Maharaj(1996)[12]提出的基于扩展的自相关系数的距离，Galeano(2000)[7]提出基于自相关的距离，Tong 和Dabas(1990)[15]提出基于残差拟合的距离，Bohte(1980)[3]提出基于交叉相关系数距离，Caiado(2006)[5]提出基于周期图的距离，Maharaj 和D’Urso(2010)[13]提出基于谱的相异度度量，Berndt 和Clifford (1996)[2]提出动态时间扭曲距离，De Gregorio(2008)[6]提出马尔科夫算子距离，等等。

时间序列聚类分析在金融领域显得尤为重要，因为金融从业人员对金融资产之间的相似性很感兴趣，通过研究资产之间的相似度，对资产进行聚类，来进行投资和风险管理。因此，金融研究者提出了很多统计方法来分析资产价格序列的相似结构。例如，Mantegna 和Bonanno(2001)[4]使用Pearson 相关系数来度量两个股票收益率序列之间的相似度。考虑到金融时间序列的波动性，Caiado 和Crato(2006)[5]提出了一种描述两个股票收益率数据之间动态特征的的类Mahalanobis 距离度量方式，并且提出了一种聚类程序来对DJIA 指数进行聚类。

本文中，通过Hoeffding’D，Kendall’sτ和Spearman’sρs三种相关系数分别来定义金融时间序列的相似度，然后运用PAM、agnes、diana 三种聚类方法对相异度度量矩阵进行聚类，从而对不同的相似度度量方法和聚类方法进行比较。这对实际中进行金融时间序列分析有借鉴作用。

文章结构分为四个部分，第一部分介绍几种了相关系数和相异度度量方法；第二部分介绍了几种聚类方法和聚类评价标准；第三部分运用股票收益率数据进行了实证分析；第四部分做出总结并提出相关建议。

一、相关系数和相异度度量

在对金融时间序列数据进行聚类之前，首先要获得适合于聚类算法的数据结构。Kaufman 和Rousseeuw(1990)[10]提出，聚类算法的数据结构通常有两种：第一种数据结构是对象—属性的n×p 矩阵，其中矩阵的行代表对象，矩阵的列代表属性；第二种数据结构是相异度矩阵，矩阵的行和列的性质一样，代表的都是两个对象之间的相异度。本文运用的是相异度矩阵数据结构，因此首先介绍一些相关系数和相异度的概念。

（一）相关系数

相关系数是最常用的相似度的度量方式，常用的相关系数包括：Pearson 相关系数ρp，Hoeffding’D，Kendall’sτ 和Spearman’s ρs。其中Pearson 相关系数ρp是一种线性相关系数，其他三种均为非线性相关系数。由于金融时间序列不服从正态分布，而呈现的是一种厚尾分布，不适合用线性相关系数进行两个金融时间序列的相关性度量。因此，本文主要考虑后三种非线性相关系数。

1.相关系数ρp

Pearson 相关系数描述的是一种线性相关关系，相关系数的值在[- 1，1]之间，数值越接近于1 或- 1，说明两个变量相关程度越大，数值越接近于0，说明两个变量之间相关程度越小。如果ρp(X,Y)=0，则说明X 和Y 是相互独立的，反之则不成立。

2.Kendall’sτ

假设（X1，Y1）和（X2,Y2）是两个二维的随机向量，Hollander 和Wolfe(1999)[9]把Kendall 相关系数定义为：

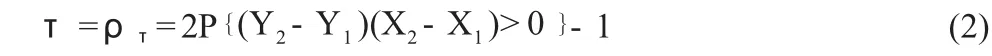
当且仅当事件{X2＞X1且Y2＞Y1}或事件{X2＜X1且Y2＜Y1}出现时，事件{(Y2- Y1)(X2- X1)＞0}才会出现。因为事件{X2＞X1且Y2＞Y1}和事件{X2＜X1且Y2＜Y1}是

互斥的，因此有：

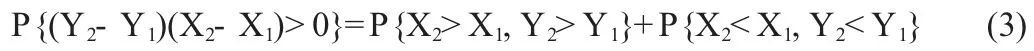
如果X 和Y 相互独立，则

同样，我们可以得到P(X2＜X1,Y2＜Y1)=1/ 4。因此如果X 和Y相互独立，则Kendall 相关系数ρτ＝2（1／4+1／4）- 1＝0，反之，则不成立。

3.Spearman’s ρs

在定义Spearman 相关系数之前，首先考虑来自二元分布中的三个独立观察值[11]：(X1，Y1),(X2,Y2)和(X3,Y3)。定义(X1,Y2)和(X2,Y3)这两个观察值之间一致

的概率：

再定义(X1- Y2)和(X2- Y3)之间不一致的概率ℓd：

用一致的概率ℓc 减去不一致的概率ℓd：

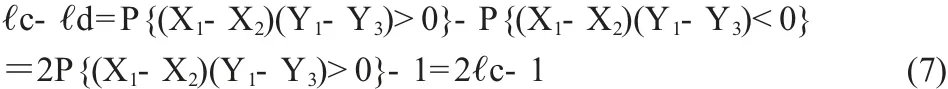
当X 和Y 独立时，则这个值是0，反之则不成立。这个值介于[- 1/ 3,1/ 3]，只有当Y 是X 的严格的单调函数时，才会取到最大值或最小值。

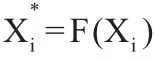
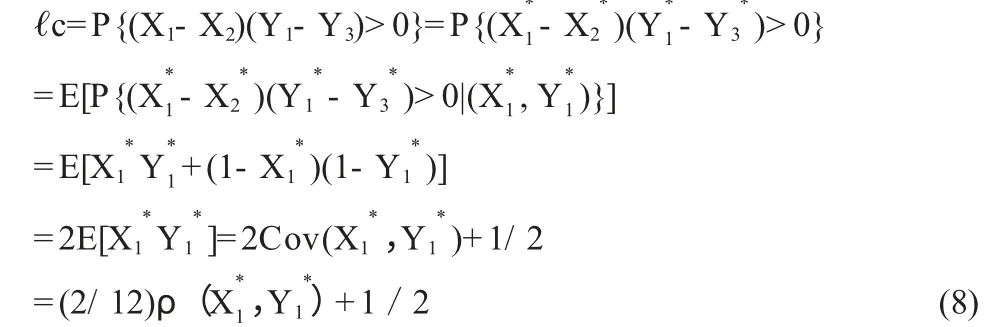
从上式可知，ℓc的取值范围在[1/ 3,2/ 3]之间，2ℓc- 1 的值在[- 1/ 3,1/ 3]之间。最终要把这个值变换到[- 1，1]之间，只需乘以3 即可：

当ρs接近于1 时，表示连个变量之间相关程度越大，当ρs接近0 时，表示两个变量之间相关程度越小，但是当ρs=0 时，两个随机变量不一定独立。

4.Hoeffding’s D

Hoeffding[8]提出了一种检验两个具有连续分布函数的随机变量是否独立的检验统计量D，这个检验统计量D 只依赖于观察值的顺序。假设(X,Y)的联合分布密度f(x,y)连续，统计量D 要解决的问题是通过随机抽取的容量为n 的样本，检验两个随机变量X，Y 之间是否独立。如果F(x,y)是一个二元分布函数，定义：

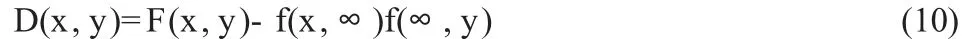
和

当且仅当D(x,y)=0 时，具有联合分布F(x,y)的随机变量X，Y是独立的。Hoeffding 还提出：0≤Δ≤1/ 30，只有当Y 是X 的单调函数时才能得到上限值1/ 30。同时Hoeffding 还提出了D 的取值范围为：- 1/ 60≤D≤1/ 30，这个值越高，X 和Y 相关程度越大。D统计量是Hoeffding 用来对两个随机变量是否独立进行检验的，因此和前面的几种相关系数都有所不同。

在实际应用中，通常把Hoeffding 系数扩大30 倍，及D*=30D，因此它的取值范围在[- 0.5,1]之间。

（二）相异度度量

以上介绍了几种常用的相关系数，但是得到的相关系数矩阵还不能直接用于聚类，要通过对相关系数进行适当的转换，使之变为能够应用于聚类算法的相异性度量。此处介绍了相似系数和相异系数，以及从相关系数到相似系数之间的转换方法。

相似系数s(i,j)表示两个对象i 和j 之间的接近程度，s(i,j)越大，两个对象就越接近。Kaufman 和Rousseeuw 认为相似度应该满足一下三个条件：

（1）0≤s(i,j)≤1；

（2）s(i,i)=1；

（3）s(i,j)=s(j,i)。

可以先计算相关系数，然后对相关系数和相似系数之间进行转换，把相关系数矩阵转换为一个相似度矩阵：

对于Hoeffding' s D 相关系数，则可以通过下式进行转换：

最终得到的s' (i,j)总是处在[0,1]之间，当s' (i,j)接近0 时，表示两者相似程度低，当s' (i,j)接近1 时，表示两者的相似程度很高。

在有些情况下则可以通过相似系数矩阵来得到相异度矩阵：

则：

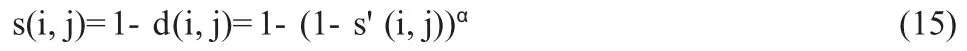
从上式可知，当α=1 时，s'(i,j)=s(i,j)，其他α 值情况下，两者不一样。通常情况下，α 可选取1/ 2，1 和2，本文中α 选取为1/ 2[1]。

二、聚类方法和聚类评价标准

（一）聚类方法

相对于基于对象- 属性矩阵的聚类方法，基于相异度矩阵的聚类方法使用范围更广，因为在很多实际情况中，获得对象之间的相异性矩阵要比取得对象- 属性矩阵要容易。因此以下主要介绍一些适用于相异度矩阵的聚类方法。

1.PAM(围绕中心点)方法。PAM 方法是一种基于划分的聚类方法，它不仅可以对对象- 属性矩阵进行聚类，也可以对相异度矩阵进行聚类，本文用于对相异度矩阵进行聚类。这种方法是由Kaufman 和Rousseeuw 提的，又被称为k- medoid 方法。

PAM 的聚类算法如下：

（1）首先选择k 个对象，这k 个对象应当为它们各自所定义的类的中心，使得每个类中其他对象到它的平均距离最短，这k 个对象被称为代表性对象。从这可知，最初的k 个代表对象不是随机选择的，这也是这种方法和k- means 方法的主要不同点。

（2）把剩余的对象归到离它最近的代表对象的一类。

Kaufman 和Rousseeuw 认为这种方法在对有离群值的对象进行聚类时，比k- means 方法更好，而且k- means 方法不能对相异度矩阵进行聚类，它只能对对象- 属性矩阵进行聚类。但是k- medoid 方法一般适用于对具有球形形状的类进行聚类，而不适用于对长条形的类进行聚类。

2.anges（层次凝聚）方法。由Kaufman 和Rousseeuw 提出的另外一种方法是agnes 方法，这是一种凝聚的层次聚类算法，即一开始分别把每个对象分为一类，聚类每进行一步，就把上次聚类结果中的两个类又聚为一个类，直到最后把所有的对象归为一个类。这种聚类方法既适用于对象- 属性的矩阵，也适用于相异度矩阵。

anges 方法的算法为：

（1）首先把两个最近的类归为一个类。

（2）在后来的每一个步骤中，最近的两个类又被聚成一类，此处两个类之间的相异度度量基于类间对象的相异度度量。

Kaufman 和Rousseeuw 提出了四种定义类间距离的方法：Average linkage，Single linkage，Complete linkage 和Ward' s Method，本文运用Average linkage 和Ward' s Method 这两种方法，分别记为agnesA 和agnesW。

3.diana（分裂层次聚类）方法。diana 方法是一种分离的层次聚类法，聚类程序和anges 方法相反。首先，把所有的对象归为一个类，然后把距离最远的两个类分开，直至所有的对象都分别分为一类。

聚类程序如下：

（1）首先，找到和其他对象的平均相异度最大的一个对象。

（2）然后，把一个对象从一个类移动到另一个类，这儿移动的根据是移动对象和剩余的类的距离和分出去的类的聚类。若前者大于后者，则移动。

（3）最后，把类规模最大的一个类进行分割。

diana 方法适用于处理球形的类的聚类，既可以对对象- 属性矩阵进行聚类，也可以对相异度矩阵进行聚类。

（二）聚类评价标准

在得到聚类结果以后，需要对得到的结果进行评价，可以根据评价标准选择聚类数，然后在给定聚类数的情况下，选择最好的聚类方法。现有有很多种统计量可以对不同的聚类结果进行评价，如ASW，CH，PH，g2,g3,cRand。根据在不同的聚类数目下的统计量的性质，有两种方法来定义最好的聚类方法。第一种方法：如果随着聚类数目的增加，统计量未呈现出一种增加或减少的趋势，那么统计量的值最大或最小的方法是最佳的聚类方法。第二种方法：如果随着聚类数目的增加，统计量呈现出一种递增或递减的趋势，则统计量在相应的聚类数目有一个显著的局部变化的方法为最佳的聚类方法，其中出现显著局部变化的这个点被称为一个关节点。下面只介绍一种常用的验证统计量ASW(average silhouette width)。

Kaufman 和Rousseeuw 提出了“silhouette- width”的定义：对于数据集中的一个对象i，它是类Ck中的一个对象，i 的silhouette- width 为：

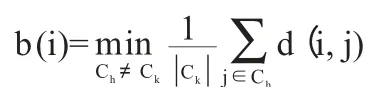
其中是i 到Ck中的其他对象的平均相异度。是i 到和它距离最近的类Ch≠Ck中的所有对象的平均距离。

Ch被称为i 的邻类，除了Ck，Ch将是距离i 最近的一类。s(i)的值在[- 1,1]之间，当s(i)接近1 时，说明类内的相异度a(i)比类间最小的相异度还要小得多，此时对象i 被正确地分类。当s(i)接近0 时，聚类结果不清晰，此时对象i 到自己类的距离和到邻类的距离几乎相等。当i 接近- 1 时，说明i 被错误分类。ASW 值越大，说明聚类的结果越好。

三、实证分析

本文选取了我国股市中房地产、金融、医药、通信、交通运输、能源、电力7 个不同行业的股票数据，总共有44 个公司。采用的数据是从2010 年1 月1 日到2013 年1 月1 日的每家公司股票的日收盘价，总共记录729 个交易日。数据来源为国泰安CSMAR 数据库。首先通过以下的方法把股票日收盘价转化为股票收益率：

以下的结果是基于股票日收盘价的对数收益率来进行的。

然后计算两个股票之间的相关系数，这样可以对相异性程度进行量化。由于金融时间序列不服从多元正态分布，因此此处不应该用Pearson 相关系数，而是运用一些非参数的相关系数，如Hoeffding’s D，Kendall' sτ 和Spearman’sρ。为了选择最好的聚类方法和最合适的聚类数目，本文中运用的检验统计量为Average silhouette width（ASW）。

图3.1 基于Hoeffding’s D 的聚类结果

从图3.1 中可以看出，当对由Hoeffding’s D 变换而来的相异度矩阵进行聚类时，在ASW 的验证标准下，agnesA 方法的ASW值开始成递增的趋势，增加的速度比较缓慢，在k=7 处达到了最大值，此后呈递减趋势，因此可知agnesA 方法的最佳聚类数为k=7。diana 方法始终呈现出一种递增的趋势，因此最佳聚类数目在ASW值最大处取得，即k=8。由于agnesW 方法是一种针对欧几里德距离矩阵进行聚类的方法，因此，在此处的聚类结果并不可靠，只作为一种参考。PAM 方法的ASW 值在k=7 时达到最大值，而且此时出现了一个明显的峰值，因此，PAM 方法的最佳聚类数目也为7。综上，对Hoeffding 进行聚类的结果可知，最终的聚类数目为k=7，在四种聚类方法中，最佳的聚类方法为PAM 方法，因为此方法的ASW 值在k=7 时有一个明显的峰值，而其他方法都没有出现明显的峰值点。

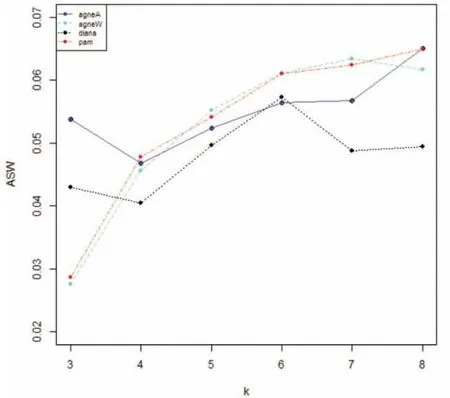
图3.2 基于Kendall’sτ 的聚类结果

从图3.2 中可以看出，agnesA 方法和diana 方法对Kendall 的聚类结果在ASW 的验证标准下，当聚类数目k 从3 到4 时，ASW值有一个明显的下降，从4 到6 时，两种聚类方法的ASW 值都呈增加趋势，到k=6 时，agnesA 的ASW 值还继续增加，但是增加的幅度不大，而diana 方法呈现明显的下降，在k=6 的地方出现一个明显的转折点。而agnesW 方法和PAM 的ASW 值一直呈现一种递增的趋势，在k=3 到k=6 时ASW 值增加的速度很快，而k=6 之后增加的幅度减少，在k=6 时出现一个转折点。综上，可以的出对Kendall 的聚类结果中最佳聚类数目为k=6，最佳聚类方法为diana方法。

图3.3 基于Spearman’sρ 的聚类结果

从图3.3 中可以看出，聚类数目从3 到7 时，agnesW 和PAM方法的ASW 值呈现出一种上升的趋势，在k=7 之后，agnesW 方法的ASW 值处于一种水平状态，而PAM 方法的ASW 值则呈现下降的趋势，在k=7 处出现一个明显的峰值。而agnesW 和diana 方法的ASW 值从k=3 到4 时，有一个微小的下降，此后agnesA 的ASW 值呈现明显的上升趋势，在k=7 处ASW 值达到最大，而diana 方法的ASW 值在k=8 处达到最大。综上，对的聚类结果中最佳聚类数目为k=7，最佳的聚类方法为PAM 和agnesA 方法。

综合以上对三种相关系数的聚类结果，可得最佳的聚类数目k=7，PAM 方法在三种相关系数聚类结果中表现优于另外几种聚类方法，在对Hoeffding‘D 相关系数进行聚类时，PAM 方方法的结果最好，下表给出当用PAM 方法对Hoeffding’D 进行聚类的结果。

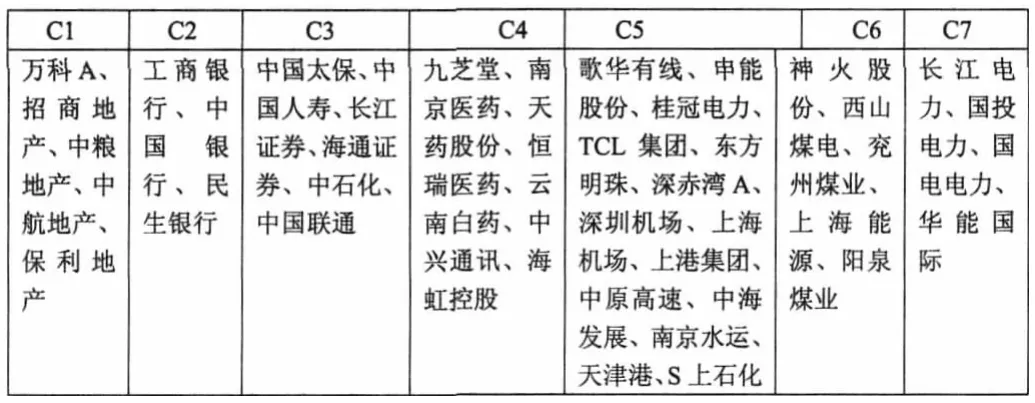
表1 用PAM 方法对Hoeffding’D 聚类为7 类时的结果

从上表中可以看出，聚类结果的第一类为房地产行业，第二类和第三类属于金融行业，第四类属于医药行业，第五类属于运输行业，第六类为能源行业，第七类为电力行业。其中第五类中的错分率比较高，但是所有运输行业的公司均在此类中，因此可以把它看为运输行业。聚类结果中，虽然有些行业的分类情况和初始分类不一致，但是很多公司的分类是一致的。说明同一个行业的公司之间收益率相关程度很高。

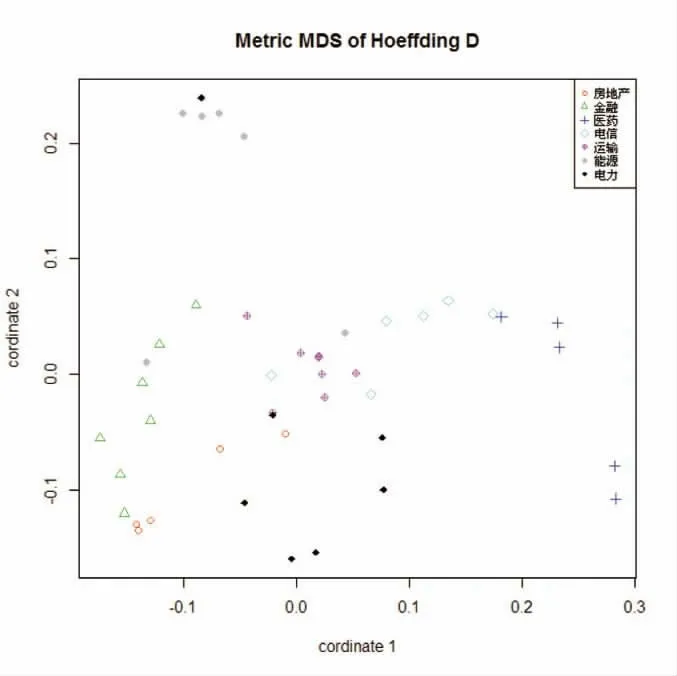
图3.4 基于Hoeffding’s D 的多元尺度图

图3.4 通过多元尺度图使得通过Hoeffding’s D 度量的公司之间的相似度在二维空间可视化。可以看出，在二维空间中，除了电信行业和运输行业外，其他各个行业得到很好的区分。

四、结论

以上通过对股票收益率进行聚类，在ASW 的评价标准下，把44 家公司聚为7 个类。从聚类结果可知，属于同一个行业的公司几乎被聚在同一个类中，只有个别公司聚类结果和所属行业不一致。因此得出结论：属于同一个行业的公司股票收益率相似程度比较大，而属于不同行业的公司股票收益率相似程度比较小。从描述相似度的三种相关系数来看，Hoeffding D 和Spearman 相关系数的结果要优于Kendall 相关系数的结果，因为针对两者的聚类结果比较明显，而针对Kendall 相关系数的聚类结果不清晰。最后，通过比较三种不同的聚类方法，可知PAM 方法对收益率序列的聚类结果要优于agnes 和diana 两种聚类方法。

文中对金融时间序列的相关性度量采用的是一些比较简单的相关系数，而且这些相关系数描述的是整个金融时间序列的相关情况，然而在实际情况中，我们更加关心的是出现亏损时候的序列之间的相关情况，因此可以通过研究金融时间序列的尾部相关情况来进行更进一步的分析。

[1]Ana Teresa YanesMusetti.2012,Clustering methods for financial time series.Seminar for Statistics.1-74.

[2]Berndt, DJ and Clifford,J.1996,Finding patterns in time series：A dynamic programming approach [J].In Advances in Knowledge Discovery and Data Mining,229-248.

[3]Bohte,ZD.Cedar,D.andKosmelu,K.1980,ClusteringofTimeSeries[J].COMPSTAT 80：587-593.

[4]Bonanno,G,Lillo,F and Mantegna,R.2001,High-frequency crosscorrelation in a set of stocks[J]. Quantit.Finance,1：96-104.

[5]Caiado,J.Crato,N and Pe?a,D.2006,A periodogram-based metric for time series classification [J].Comput.Statist.Data Anal.,50：2668-2684.

[6]De Gregorio,A and Iacus,SM.2008,Clustering of discretely observed diffusion processes[J].Comput.Statist.Data Anal.,54：598-606.

[7]Galeano,P and Pe?a,D.2000,Multivariate analysis in vector time series[J].Resenhas,4：383-404.

[8]Hoeffding.W.1948,A non-parametric test of independence.The Annals of Mathematical Statistics,19(4)：546-557

[9]Hollander.M.andD.Wolfe.1999,Nonparametric Statistical Methods.John Wiley&Sons.

[10]Kaufman.L.andP.Rousseeuw.1990,Finding groups in Data：An Introduction to Cluster Analysis,John Wiley and Sons,Inc.

[11]Kruskal.W.1958,Ordinal measures of association.Journal of the American Statistical Association.,284(53)：814-861.

[12]Maharaj,EA.1996,A significance test for classifying ARMA models[J].J.Statist. Comput.Simul., 54：305-331.

[13]Maharaj,EA and D'Urso,PA.2010,A coherence-based approach for the pattern recognition of time series [J].Physica A：Statist.Mech.Applic.,389：3516-3537.

[14]Piccolo,D.1990,A distance measure for classifying ARIMA models[J].J.Time Ser.Anal.,11：152-164.

[15]Tong,H and Dabas,P.1990,Cluster of time series models： An example[J].J.Appl. Statist.,17：187-198.