大功率高频X波欠密加热电离层的理论与数值模拟
2013-08-11郝书吉李清亮杨巨涛吴振森
郝书吉,李清亮,杨巨涛,吴振森
1 西安电子科技大学理学院,西安 711071
2 中国电波传播研究所青岛分所,青岛 266107
1 引 言
在电离层中传播的高频(HF)电波具有两种独立的特征波模形式:右旋圆极化波(简称O波)和左旋圆极化波(简称X波).早期的大功率高频电波加热电离层理论[1-2]和实验结果表明[3-6]:当采用 O 波加热时,在位于泵波反射高度和上混杂共振高度之间的谐振层内可以发生谐振和波模转换,导致局部显著的电离层人工变态—电子温度和电子密度的有效改变;而采用X波加热时,由于其反射高度低于谐振高度,加热只能引起电离层比较微弱的扰动.因此在很长的一段时间内,X波加热电离层技术一直不被国内外学者所重视.
20世纪90年代以来,随着加热装置性能的提升(如有效辐射功率得到提升、加热参数的设置更加灵活),X波加热电离层技术得到了持续的关注.Frolov利用Sura加热站开展实验发现[7]:当加热系统同时辐射O波和X波,并且O波和X波的反射高度相同(满足条件fHX=fHO+0.5fce,fHO和fHX分别为O/X波的频率,fce为电子回旋频率)时,X波可显著减弱O波加热引起的电离层扰动,尤其是减小小尺度人工沿场不规则体(Artificial Field-Aligned Irregularities,简称 AFAIs)的横向尺寸.此后在高频主动极光研究计划(High Frequency Active Auroral Research Program,简称 HAARP)开展的加热实验[8]也验证了这一现象.
目前,大功率高频X波加热理论研究集中在低电离层 ELF/VLF调制[9-12]加热方面,高电离层 X波加热则以实验研究为主,Lofas和Gustavsson等[13-14]通过实验发现,在X波欠密加热电离层条件下,电子温度在电离层相当宽的高度范围内都有较大的增加,但所观察的电子密度和离子温度并没有发生变化;并从理论上简单解释了不同功率等级下实验现象(加热前后电子温度变化).在此基础上,本文利用电离层中电子的加热与冷却物理机制,深化X波欠密加热的物理过程,并构建X波欠密加热理论仿真模型,对已知相关实验现象进行解释,同时利用此模型,分析和研究加热效果与加热参数和背景电离层状态的相互关系,为X波加热实验提供理论参考.
2 X波欠密加热理论模型
利用大功率高频电波进行电离层加热时,在电波传播的整个路径上,由于碰撞效应电子的电导率不为零,使得电子从入射高频电波中迅速获得能量,电波则受到碰撞阻尼,这就是欧姆加热过程.先前关于过密加热条件下欧姆加热效应研究较多,在这种条件下,泵波能量主要消耗在电波反射高度以下,加热效应主要沿着地磁场方向传导.由于电波与等离子体波的相互作用过程主要集中在电波反射高度附近,很难单独区分欧姆加热和非线性谐振加热过程,除非有效辐射功率低于激发非线性阈值.当采用X波欠密加热加时,在电离层高度上不存在驻波,X波也不可能到达反射高度或上混杂谐振共振高度,因此不会有谐振过程发生.因此,X波欠密加热过程的研究对于深入了解较宽电离层高度范围内的欧姆加热效应具有重要意义.
在X波欠密加热电离层时,在电离层高度上不存在加热频率等于上混杂频率或等离子频率的高度,因此其加热过程中不存在上混杂谐振过程.实验[8-9]现象也表明,在X波欠密加热过程中电子密度和离子温度没有发生改变.基于此特点,仅考虑电子的能量方程[5,15-17]:

其中kB为波磁曼常数,Te为电子温度,ne为电子密度,Q0为吸收背景能量(即不加热时,电离层稳态是电离层吸收的能量,如太阳能等)的能量密度,QHF为单位时间内吸收入射波能量的能量密度,Le为单位时间内能量损耗(电子与离子和中性粒子的弹性碰撞、非弹性碰撞的能量损耗)的能量密度,地磁场方向为s,与垂直方向z有关系式=sinI,I为磁倾角为热传导张量.方程左边第一项是由于HF外场加热引起的电子温度随时间的变化,第二项是对流项,第三项是压缩项.由流体力学的知识可知,(1)式左边方括号里面为基本的欧拉方程的一部分,第一项为局部导数项,与电子随机热速度的变化有关,在加热过程中随机热速度变化迅速,第二项为迁移导数项,其中ve为等离子体的整体漂移速度,受到偶极扩散的限制,因此迁移导数项远小于局部导数项,即(1)式中对流项的贡献可以忽略;同时压缩项在F层加热计算中也可以忽略[18],沿着背景电离层磁场方向的热传导率 (Ke∥)要远大于垂直方向,(1)式可以化简为:
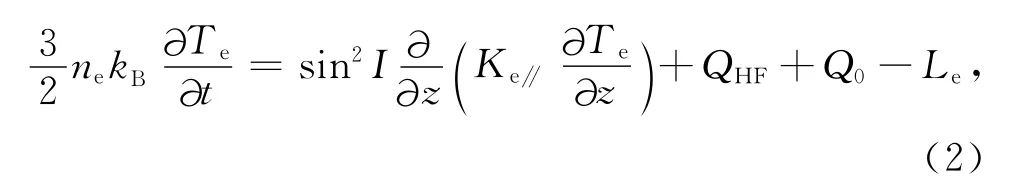
沿磁场方向热传导系数Ke∥的计算式为[2]

其中Ke∥的单位为eV·cm-1·s-1·K-1,α表示中性粒子的种类(为O2,N2和O),nα为中性粒子α的数密度,为相应中性粒子的平均动量传输截面,其表达式为[1]:ε0为自由空间介电常数,e表示电子电量,lnΛ为库仑

对数,可表示为[19]

其中

其中zi表示原子电荷,lnγ=0.577为欧拉常数,ni为离子(NO+,O+2和O+)的数密度,Ti为离子的温度.
电子能量损耗Le可近似为[19]

Le的单位为eV·m-3·s-1,ne,i的单位 m-3.
入射波能量吸收QHF表达式为[2]

其中E±(z)表示入射波电场,σ±(z)表示电离层电导率张量,下标“+”表示O波,“-”表示X波.电场E±(z)的高度分布为

其中z0表示电离层底部高度,ε±(z)表示电离层高度z上的介电常数张量.N±(z)为电离层折射指数,k0=ω/c,电离层底部电场E(z0)可近似为[20]

电场单位为V/m,其中ERP为加热系统的有效辐射功率.
由于加热效应主要沿着地磁场方向传导,因此电离层折射指数N±(z)与σ±(z)和ε±(z)的关系式为[2]
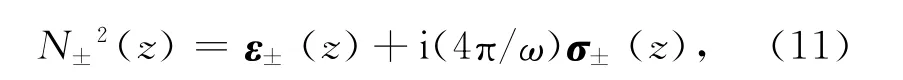
其中

式中ve为电子的碰撞频率,ω为加热波频率,ωp为等离子频率,ωc为电子的回旋频率.电子的碰撞频率(ve)包括电子与中性粒子的碰撞频率(ven)和电子与离子的碰撞频率(vei),即[21]

由以往的实验结果[6]和物理仿真模型[1],在模拟仿真X波欠密加热时,取边界条件为下边界电子温度不变,上边界电子温度梯度不变.低电离层对入射波的吸收损耗为4dB,空间步长dh= (1/sinI),单位km,时间步长dt=5ms,背景电离层参数和中性大气参数分别由国际参考电离层模型IRI-2012和MSIS90经验模式给出.
根据式(8)—(13),在相同的加热参数下,欠密加热电离层时,O波与X波能量吸收QHF的高度剖面对比如图1所示.

图1 O波与X波欠密加热电离层QHF的高度剖面对比Fig.1 QHFheight profile of O wave and X wave under-dense heating the ionosphere
从图1可以得出,在相同的加热参数条件下,欠密加热电离层时,X波能量吸收项QHF是O波能量吸收项的4倍左右,即X波加热引起电离层电子温度扰动要远大于O波引起电离层电子温度的扰动,这也是国外欠密加热实验中主要采用X波的一个主要原因.
3 数值仿真结果
3.1 实验结果与仿真结果对比
Lofas等[13]首次利用EISCAT加热装置进行X波欠密加热的实验中发现:电离层F层高度区域上电子温度都有增加,温度最大变化为300~400K(如图2所示).实验期间采用的加热参数为:系统有效辐射功率为180MW,加热频率(fHF)为4.04MHz.实验期间电离层临频(f0F2)变化范围为2.1~3.1MHz,相应的X波临频(fXF2)变化范围为3.0~4.01MHz.为验证本文建立的理论模型,采用与实验相同的加热参数(ERP=180MW,fHF=4.04MHz),并选择与实验期间(某一时刻)相近的背景电离层参数(f0F2=2.3MHz,fXF2=3.1MHz)进行仿真,实验结果与仿真结果对比如图2所示.
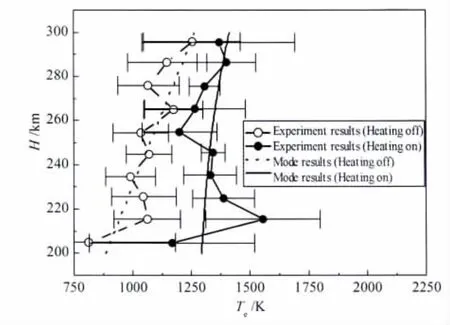
图2 实验结果与仿真结果对比Fig.2 Contrast of experimental results and simulation results
图2表明:实验结果与仿真结果接近,但又不完全吻合.这是因为图2给出的实验结果为实验期间(一段时间内)电离层各高度上电子温度的平均值,同时图2的实验结果中也给出了该时段内电离层各高度上电子温度变化的误差范围;而图2的仿真结果是针对该时间段内某一时刻的背景电离层参数进行的理论计算,其模拟结果处于实验结果给出的电子温度误差范围内.同时,从图2仿真结果可以看出,在电离层215km处,电子温度变化约400K,相对增量约40%;随着高度的上升,温度变化量减小.仿真结果与实验结果一致,说明本文建立的理论模型是正确的,可用于电离层X-mode欠密加热数值模拟研究.下面本文将利用此模型研究加热参数和背景电离层参数对X-mode欠密加热电离层F层的影响.
3.2 加热参数对X-mode欠密加热效果的影响
图3是加热功率对X波欠密加热效果影响的仿真结果,选取的加热地点为tromsΦ(EISCAT),背景电离层X波临频约为5.2MHz,加热频率为5.8MHz.
图3计算结果表明,随着加热功率的增加,各高度上电子温度的变化量均增大,但二者并不是线性增加关系.如在电离层220km处,加热功率为50MW时,电子温度增加4%;当加热功率变为500MW时,电子温度增加38%;当加热功率为1000MW时,电子温度增加60%.这是因为加热系统的辐射功率越大,在各高度上电波能量转移到电离层中就越大,引起电子温度的扰动也就越大.此外,当有效辐射功率较小时,各高度上电子温度随加热功率增大增加较明显,且一定高度范围内,加热高度越低时电子温度增加越大.如加热功率为180MW时,200km处电子温度增加约300K,300km处电子温度增加约100K.这与文献[9]实验结果一致(二者的背景电离层条件相近).

图3 加热功率对加热效果的影响(a)不同功率等级下电子温度的高度剖面;(b)不同高度下电子温度变化量(ΔTe)随功率的变化.Fig.3 Heating effects with varying heating power(a)Electronic temperature height profile of different heating power;(b)Electronic temperature variation(ΔTe)with varying heating power of different height.
在背景电离层条件不变和加热功率不变(ERP=300MW)的情况下,改变加热频率,研究加热效果与加热频率的关系.图4给出了加热频率(临频不变)对电子温度变化量影响的数值仿真结果.可以看出,增大加热频率(图4中加热频率与X波临频比值增大),电子温度的增加量减小;加热频率在X波临频附近时,加热频率的增加引起电子温度的增加量迅速减小,加热频率远离X波临频时,加热频率的增加引起电子温度的增加量减小趋于平缓.主要原因是,欠密加热时电离层最显著的变化是由电离层中的碰撞过程和输运过程共同决定,电离层的吸收损耗和入射频率在增量上具有相反的趋势,即频率愈高,电离层吸收损耗愈小,电波能量转移到电离层中的愈少,电子温度的变化就愈小.

图4 不同高度处加热频率与临频比值(fHF/f0F2)对电子温度变化量的影响Fig.4 Electron temperature variation change with ratio of heating frequency to critical frequency
3.3 背景参数对加热效果的影响
对比图2和图3可以发现,在相同的加热功率(180MW)条件下,电离层电子温度的扰动变化量并不相同,在215km高度处,前者约为400K,后者约为300K.其原因主要是由于两种情况下的背景电离层参数(主要是背景电子密度和电子温度)不同.下面分析背景电子密度和电子温度对加热效果的影响.
图5和图6分别给出不同背景电子密度和电子温度下的加热结果.选取的加热地点为tromsΦ,其中加热系统的有效辐射功率为300MW,背景电离层X波临频为5.2MHz.对于不同背景电子密度情况,由于电离层临频也不相同,为满足相当加热条件(取加热功率相同,加热频率与临频比值相同),加热频率取X波临频的1.05倍;对于不同背景电子温度情况,加热频率取5.4MHz.

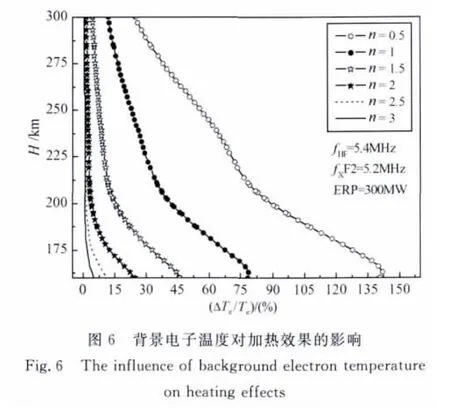
图5中N表示不同情况下背景电子密度与参考电子密度(N=1)的比值(考虑到实际情况,在仿真计算中N最大取值为2).计算结果表明,当N=0.5时,电子温度最大相对变化量由约75%变为约135%,而当N=2时,电子温度相对变化量减小到约40%.由此得出,利用相当的加热条件,在背景电子密度较小时开展加热实验,相对于背景电子密度较高时可获得更好的加热效果.图6中n表示不同情况下背景电子温度与参考电子温度(n=1)的比值(考虑到实际情况,在仿真计算中n最大取值为3).计算结果表明,当n=0.5时,电子温度最大相对变化量由约78%变为约140%,而当n=3时,电子温度相对变化量减小到约3%.由此得出,在相同的加热条件下,背景电子温度越低,加热效果越好.
因此,背景电离层电子密度和电子温度越大加热效果越弱,这是由于电子密度和电子温度越大,初始背景能量吸收项Q0和能量损耗项Le越大,在入射波能量不变的情况下(QHF不变),加热引起的温度变化也就越小[15];同时,背景电离层的电子密度和电子温度越大,背景电子密度梯度和电子温度梯度也越大,在一定加热能量下,温度的扰动量也就减小.因此,在背景电离层电子密度和电子温度较低时的夜晚开展X波欠密加热实验相对于白天可获得更好的加热效果.
3.4 高/低纬度地区加热效果分析
一般情况下,高/低纬度地区加热效果会存在差异,其本质是背景电离层状况不同,由于高纬度地区和中低纬度地区地理位置的差异,导致不同地区磁倾角不同,而磁倾角直接影响X波欠密加热模型(公式(2))中右边第一项(热传导项)的大小.图7a和图7b分别是tromsΦ(EISCAT)(19.2°E,69.6°N)、青岛(120.1°E,36.0°N)、桂林(110.1°E,25.2°N)和Arecibo(67.0°E,18.0°N)背景电子温度和在相当的加热条件下(加热功率同为300MW,加热频率为X波临频的1.05倍)电子温度变化的高度剖面.
由图7可知,同一时刻不同地区的背景电子密度不同,高纬tromsΦ地区的背景电子温度要低于其他中低纬地区;桂林和Arecibo两地背景电子温度相差不大.图7b中的计算结果表明,在相当的加热条件下,tromsΦ(EISCAT)的加热效果要远强于其他地区,同时必须指出的是同一时刻tromsΦ(EISCAT)的临频也最小,即电子密度最小;桂林的加热效果略强于Arecibo,原因是同一时刻桂林的背景电子密度要小于Arecibo;青岛的背景电离层温度处于中间位置,其加热效果也处于中间.结合上述分析可知,在相当的加热条件下,开展X波欠密加热,高纬度地区加热效果要优于中低纬度地区.

图7 不同地区加热效果对比(a)不同地区背景电子温度对比;(b)不同地区电子温度相对变化量高度剖面.Fig.7 Heating effects of different districts(a)Background electron temperature of different districts;(b)Electron temperature relative variation of different districts.
4 结论和讨论
本文根据X波欠密加热情况下大功率无线电波与高电离层的相互作用特点,从电离层中电子的加热机制出发,构建了基于X波欠密加热的理论仿真模型,理论推算和数值模拟结果表明,采用X波欠密加热时,
(1)加热功率增加,加热效果增强.如在特定背景参数下,加热功率为50MW时,电子温度增加4%,加热功率为1000MW时,电子温度增加60%;
(2)一定频率范围内,随加热频率增加加热效果减弱.加热频率在X波临频附近,加热频率的增加引起电子温度的增加量迅速减小,加热频率远离X波临频时,加热频率的增加引起电子温度的增加量减小趋于平缓;
(3)在相当的加热条件下,背景电子温度越低、电子密度越小加热效果越强,高纬度地区加热效果要优于中低纬度地区.
本文建立的X波欠密加热理论模型可用于对相关实验结果进行预测和实验参数的选择提供参考.根据本文结论,为获得更加有效的加热效果,可增大加热系统的有效辐射功率、或根据实时背景临频选择合适的加热频率、或在电离层背景温度较低密度较小时(日出前后或日落前后)开展加热实验等.
过密加热条件下电波与等离子体波的相互作用过程主要集中在电波反射高度附近,很难单独区分欧姆加热和非线性谐振加热过程,除非有效辐射功率低于激发非线性阈值,因此,X波欠密加热过程的研究对于深入了解较宽电离层高度范围内的欧姆加热效应具有重要意义.此外,由于X波欠密加热过程中没有改变背景电离层的电子密度,只增加了背景电离层电子温度,因此它可以作为其他加热模式的预加热来研究不同背景温度下加热效应.如O波加热产生受激电磁辐射(SEE)实验中,先用X波欠密加热,提升背景电子温度,增加背景电子温度和离子温度的比值,可有效增强O波过密加热阶段SEE的激发[22].
另一方面,当X波加热频率(fHX)位于O波临频(f0F2)和 X 波临频(fXF2)之间时[23],在加热波反射高度处电子温度增加50%(同样条件下O波加热时电子温度最大只增加33%),同时在很宽的高度范围内电子密度都有较大的增加.对于这一实验现象,目前还没有比较完备的理论去解释,单从实验现象来看,它既符合欧姆加热某些特点(如电子温度在很宽范围内增加),又符合谐振加热的某些特点(电子密度具有较大的增加).其加热过程是一个复杂过程,可能存在多种机制,其具体的加热机理将是下一步要研究的问题.
(References)
[1]Hansen J D,Morales G J,Maggs J E.Large-scale HF-induced ionospheric modifications:theory and modeling.J.Geophys.Res.,1992,97(A11):17019-17032.
[2]Shoucri M M,Morales G J,Maggs J E.Ohmic heating of the polar F region by HF pulses.J.Geophys.Res.,1984,89(A5):2907-2917.
[3]Utlaut W F,Violette E J.A summary of vertical incidence radio observations of ionospheric modification.Radio Sci.,1974,9(11):895-903.
[4]Inhester B,Das A C,Fejer J A.Generation of small-scale field-aligned irregularities in ionospheric heating experiments.J.Geophys.Res.,86(A11):9101-9106.
[5]Kuo S P,Lee M C.On the parametric excitation of plasma modes at upper hybrid resonance.Phys.Lett.A,1982,91(9):444-446.
[6]Hansen J D,Morales G J,Duncan L M,et al.Large-scale HF-induced ionospheric modifications-experiments.J.Geophys.Res.,1992,97(A1):113-122.
[7]Frolov V L,Kagan L M,Sergeev E N,et al.Ionospheric observations of F region artificial plasma turbulence,modified by powerful X-mode radio waves.J.Geophys.Res.,1999,104(A6):12695-12704.
[8]Hysell D L,Nossa E,McCarrick M.X-mode suppression of artificial E region field-aligned plasma density irregularities.Radio Sci.,2011,46(2),RS2010,doi:10.1029/2010RS004551.
[9]汪枫,赵正予,张援农.低纬地区电离层电流的人工调制数值模拟.地球物理学报,2009,52(4):887-894,doi:10.3969/j.issn.0001-5733.2009.04.004.Wang F,Zhao Z Y,Zhang Y N.Numerical modeling of ionospheric current artificial modulation at low latitude.Chinese J.Geophys.(in Chinese),2009,52(4):887-894,doi:10.3969/j.issn.0001-5733.2009.04.004.
[10]常珊珊,赵正予,汪枫.电离层人工调制激发的下行ELF/VLF波辐射.地球物理学报,2011,54(10):2458-2467,doi:10.3969/j.issn.0001-5733.2011.10.003.Chang S S,Zhao Z Y,Wang F.The downward ELF/VLF waves radiation excited by ionospheric artificial modulation.Chinese J.Geophys.(in Chinese),2011,54(10):2458-2467,doi:10.3969/j.issn.0001-5733.2011.10.003.
[11]汪枫,赵正予,常珊珊等.电离层人工调制在水平分层电离层中所激发的ELF波辐射.地球物理学报,2012,55(7):2167-2176,doi:10.6038/j.issn.0001-5733.2012.07.003.Wang F,Zhao Z Y,Chang S S,et al.Radiation of ELF waves by ionospheric artificial modulation into a stratified ionosphere.Chinese J.Geophys.(in Chinese),2012,55(7):2167-2176,doi:10.6038/j.issn.0001-5733.2012.07.003.
[12]Stubbe P,Kopha H.Modulation of the polar electrojet by powerful HF waves.J.Geophys.Res.,1977,82(16):2319-2325.
[13]Lofas H,Ivchenko N,Gustavsson B,et al.F-region electron heating by X-mode radiowaves in underdense conditions.Ann.Geophys.,2009,27(6):2585-2592.
[14]Gustavsson B,Rietveld M T,Ivchenko N V,et al.Rise and fall of electron temperatures:Ohmic heating of ionospheric electrons from underdense HF radio wave pumping.J.Geophys.Res.,2010,115(A12),A12332,doi:10.1029/2010JA15873.
[15]Meltz G L,Holway Jr H,Tomljanovich N M.et al.Ionospheric heating by powerful radio waves.Radio Sci,1974,9(11),1049-1063.
[16]邓峰,赵正予,周晨等.高频加热中低纬电离层激励不稳定性研究.地球物理学报,2010,53(1):10-21,doi:10.3969/j.issn.0001-5733.2010.01.002.Deng F,Zhao Z Y,Zhou C,et al.Research of ionospheric instability excited in mid and low latitudes HF heating.Chinese J.Geophys.(in Chinese),2010,53(1):10-21,doi:10.3969/j.issn.0001-5733.2010.01.002.
[17]王占阁,徐彬,许正文等.极区电离层加热的数值模拟与实验对比.地球物理学报,2012,55(3):751-759,doi:10.6038/j.issn.0001-5733.2012.03.004.Wang Z G,Xu B,Xu Z W,et al.A comparison of numerical simulation and measurements during ionospheric heating.Chinese J.Geophys.(in Chinese),2012,55(3):751-759,doi:10.6038/j.issn.0001-5733.2012.03.004.
[18]倪彬彬,赵正予,项薇等.高频泵波加热电离层的数值模拟.电波科学学报,2004,19(3):274-289.Ni B B,Zhao Z Y,Xiang W,et al.Numerical modeling of ionospheric modificiation with powerful HF pump waves.Chinese Journal of Radio Science (in Chinese),2004,19(3):274-289.
[19]Schunk R W,Nagy A F.Electron temperatures in the F Region of the ionosphere:theory and observations.Rev.Geophys.,1978,16(3):355-399.
[20]Bilitza D.International reference ionosphere-status 1995/96.Adv.Space.Res.,1997,20(9):1751-1754.
[21]Banks P M,Kockarts G.Aeronomy,Part A and Part B.New York:Academic Press,1973.
[22]Hussein A A,Scales W A.Simulation studies of parametric decay processes associated with ionospheric stimulated radiation.Radio Sci.,1997,32(5):2099-2107.
[23]Blagoveshchenskaya N F,Borisova T D,Yeoman T K,et al.Artificial small-scale field-aligned irregularities in the high latitude F region of the ionosphere induced by an X-mode HF heater wave.Geophys.Res.Lett.,2011,38(8),L08802,doi:10.1029/2011GL046724.
