超高耸钢结构的模态参数识别及模型修正
2013-08-11叶锡钧安关峰周朝阳颜全胜
叶锡钧,安关峰,周朝阳,颜全胜
(1.广州市市政集团有限公司,广州510060;2.中南大学 土木工程学院,长沙410004;3.华南理工大学土木与交通学院,广州510641)
精确的有限元建模是大型工程结构健康监测、损伤诊断的必要基础。尽管有限元方法得到了高度的发展,但有限元的理论参数常常与从结构实测模态参数不一致。因此,必须对结构理论模型进行调整或修正,使得修正后结构分析的模态参数与实测值一致,以供后续结构健康监测、损伤诊断研究之用[1]。然而,准确获取大型工程结构的准确模态参数是首要问题。近十几年来,基于环境激励的结构模态参数识别研究一直是土木工程领域十分活跃的课题,因为其具有不用打断结构的正常使用、无需昂贵的激励设备、只需测定结构的动态响应等特点。环境振动测试的方法不仅己经成功地应用于一些桥梁的动力试验中,也成功地应用于一些高耸结构的动力试验中[2]。
笔者基于GNTVT Benchmark[3]的实测数据,运用3种不同的仅基于输出响应的模态参数识别方法识别出了真实结构的前十二阶模态参数,并与ANSYS有限元模型的计算结果做了详细的比较。最后,利用遗传算法对GNTVT初始有限元模型进行参数修正。
1 GNTVT Benchmark简介
1.1 GNTVT健康监测系统
广州新电视塔高610m,由一座高达454m的主塔和一个高156m的天线桅杆构成(图1(a))。主塔是由钢结构外筒和钢筋混凝土核心筒组成的筒中筒结构体系。外筒由24根钢管混凝土柱和46个椭圆形钢环梁及钢斜撑组成。
倪一清等在广州新电视塔上布置了一套健康监测系统,并提出针对高耸柔性结构的结构健康监测Benchmark[3]。图1(b)为广州新电视塔监测系统配置图。该监测系统在塔身8个不同高度的位置处共配置了20个伺服式单向加速度计。其中,在第4与第8个高度位置处配置了4个单向式加速度计,2个用以测量主塔内筒长轴向(y方向)的加速度,其余2个测量短轴向(x方向)加速度。在另外6个高度位置,只安装2个加速度计,分别用以测量主塔内筒长轴向与短轴向加速度。为减少由于长距离传输而造成的噪声影响,该系统采用分布式的信号采集系统。在每层设置一个采集单元采集该层的加速度数据后,再集中传输到塔底的控制室。详细的测量数据及说明可参见文献[3]。

图1 广州新电视塔外观及监测系统示意图
1.2 实测数据模态参数识别结果
笔者在文献[4]中运用 EFDD、SSI/Data和 M-NExT/ERA 3种方法对GNTVT Benchmark提供的数据进行模态参数识别,结果列于图2和表1。

图2 M-NExT/ERA识别过程的稳定图
从图中可以清晰看到在0~1.4Hz范围内有13阶频率,取前12阶模态进行研究。第1阶频率约为0.01Hz,由此可知GNTVT为刚度很柔的高耸结构,另外在0.3~0.6Hz和1.1~1.3Hz这2个频率带之间模态比较密集。
求得各种方法识别结果的平均值作为最终结果,见表1。3种方法的频率识别结果与文献[5]非常吻合,但阻尼比识别结果差异较大。其中,M-NExT/ERA和SSI/Data识别的频率和阻尼比结果较为接近,且阻尼比都呈由低阶向高阶递减的趋势;而EFDD识别的阻尼比结果比前两种方法要大,且递减趋势不明显,这与其识别阻尼比的方法有关系。

表1 GNTVT Benchmark模态参数识别结果[4]
2 GNTVT有限元模型的建模过程及模态特性
2.1 有限元模型的建立
由于GNTVT的结构异常复杂,参照文献[6-7],在建立塔体的有限元模型时做了如下的简化:
1)立柱为钢管混凝土组合结构,根据式,考虑通过弹性摸量的换算将钢和混凝土换算成同种材料的刚度形式,泊松比取0.253 9;
2)立柱、环梁和斜撑组成了钢结构外筒结构,46个环梁与水平面有一个倾斜角度(15.5°),考虑到外筒为一个网格状的整体结构,将环梁与水平放置,忽略其倾斜角;
3)核心筒为劲性混凝土结构,内部有竖向连接的墙体满足功能需要,出于减少有限元计算单元的需要,在建立有限元模型时不建立内墙单元,而通过加大核心筒外墙厚度以弥补不考虑内墙的刚度损失;
4)假定连接内外筒的楼板在平面内刚度无穷大,用板壳单元来模拟楼板,用提高材料的弹性模量的方法以考虑平面内刚度无穷大的假定,并将楼板的重量折算成材料的密度已考虑楼板的恒荷载;
5)将上部天线的重量以质量单元的形式均匀地施加到24根立柱的顶端。
钢管混凝土结构立柱、环状构件和斜撑采用梁单元Beam 188进行模拟;核心筒外墙、楼板以及内外筒的连接楼板模拟采用壳单元shell63进行模拟;采用质量单元Mass21来考虑上部天线的重量。
初始有限元模型中,混凝土核心筒外墙厚度取500mm,材料为混凝土C60;模拟楼板的shell63单元厚度取200mm,弹性模量取2.14×1015N/m2;考虑楼板的恒荷载,材料的密度取5 000kg/m3。模型共有13 425个单元,10 689个节点,见图3。

图3 GNTVT的初始有限元模型
2.2 初始有限元模型的模态特性
通过ANSYS的分块Lanczos模态分析法对GNTVT初始有限元模型进行模态分析,提取前12阶模态频率列于表2。表中实测值取表1中M-NExT/ERA的识别结果。
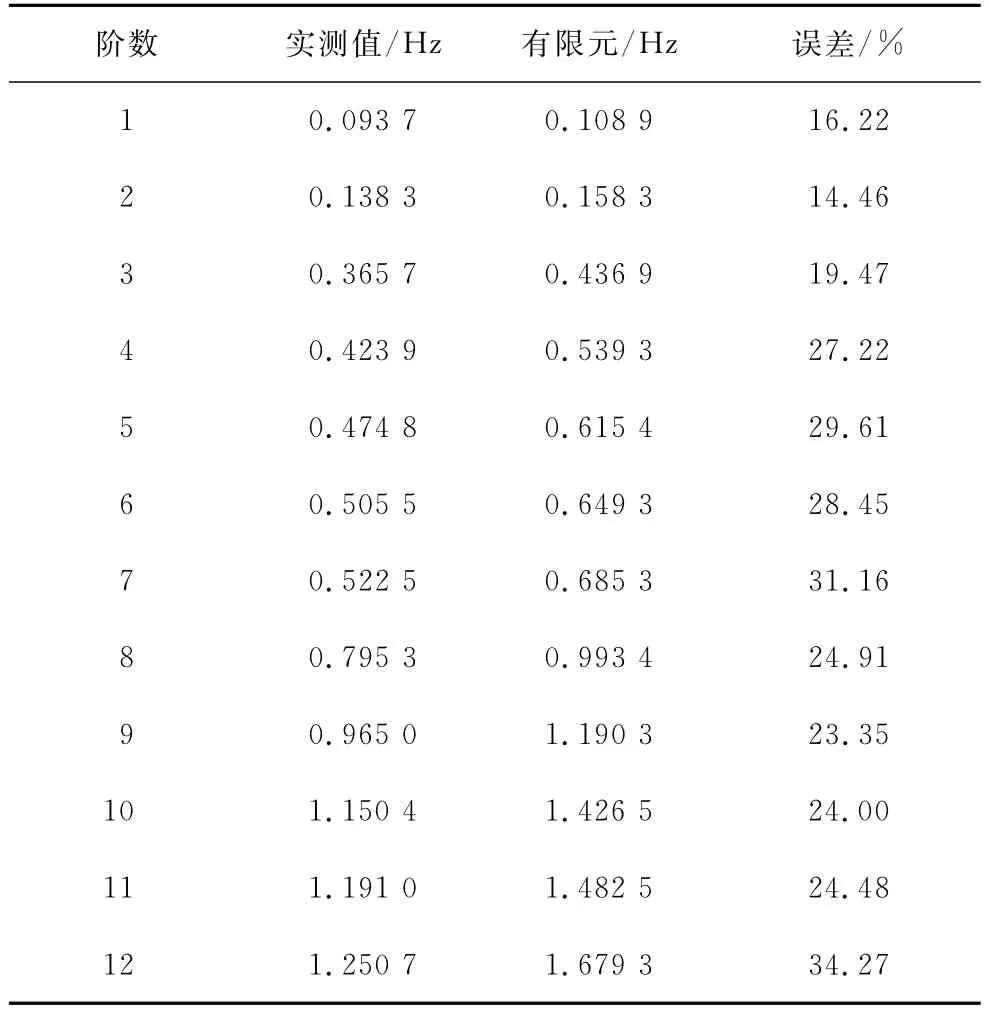
表2 GNTVT初始有限元模型的模态特性
从表中可以看出,初始有限元模型的前12阶模态频率与实测值差异较大,各阶模态频率值都比实测值要大,且阶数越高,差异越大。这是由于在建模的过程中对结构做了一定程度的简化,另外有限元模型中的各项参数是根据设计资料或假定值确定,而不是根据结构的真实状态确定的。
3 基于遗传算法的有限元模型参数修正
3.1 灵敏度分析及待修正参数的选择
一般来说,修正参数的选取有两种办法,一种是依赖工程师的经验进行选取;另一种则是在参数灵敏度分析的基础上进行选取。笔者认为选择待修正参数时,应在灵敏度分析的基础上,根据工程是经验合理地做出选择,遵循以下原则:
1)减少待修正参数的个数,将能初步确定的参数先确定下来;
2)结构模态频率的变化对所选择的待修正参数的变化较为敏感;
3)实际结构中,待修正参数需要具有一定变异性。
遵循以上原则,初定待修正的参数为:
2)核心筒混凝土的弹性模量E11和密度D;
3)核心筒外墙厚度R1、楼板厚度R2、楼板荷载密度R3。
灵敏度分析的主要问题从数学意义上可理解求导计算。设有模型Φ,其中为输出矩阵为 参 数 矢 量,为系数矩阵,则第Φ 个参数的灵敏度定义为对的一阶导数

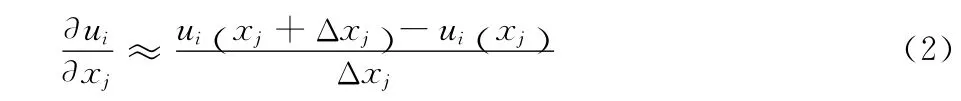
3.2 参数修正过程
选取表2中的实测值作为参考基准,使修正后模型的模态频率值与的实测值尽量接近。从一般经验来看,选择的阶数越多则模型修正的精度就会越高,但大量研究表明[9,10],参考频率阶数选择的阶数在4阶以内的,能得到很好的修正效果;而选择的频率阶数多于4阶的,并不能保证所有模态结果都精确,部分模态甚至出现误差增大的现象,除此之外修正结果还在低阶模态出现了精度偏低的现象。
这里设定适度函数为
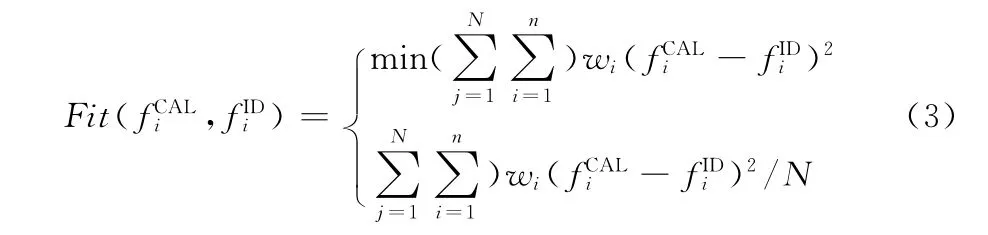

图4 初定各待修正参数的频率灵敏度
在运用遗传算法进行迭代优化计算前,为了避免修正参数的变化过大,失去结构本身的物理意义。这里先确定各参数的调整范围如表3所示。
最后,设定种群数量为20,交叉概率为0.7,变异概率为0.05。遗传算法的迭代过程如图5所示,迭代到15代的时候就已基本收敛,计算耗时约为15h。

图5 遗传算法迭代过程
最终确定的参数值如表4所示。10种立柱的换算弹性模量(E1~E10)中除了E6外,其他都减少;而核心筒外墙厚度R1、楼板厚度R2、楼板荷载密度R3、核心筒密度D都增大。从另一个角度来说,即是原始有限元模型的刚度偏大,这里通过调整结构的弹性模量和质量使得其刚度减少,频率降低。

表3 待修正参数的变化范围

表4 各参数的修正值
3.3 最终模态参数结果
表5给出了参数修正后的模型计算频率值与实测频率值的对比。修正过程设定前4阶频率的权重值均为1,5~12阶频率的权重值依次减少。修正后,前5阶频率的误差值最大为-4.11%(第2阶),最小值为0.88%(第3阶),第6~12阶频率的误差都在10%以上,可见以前5阶频率为基准的修正结果是可接受的。
值得注意的是,在遗传算法的迭代优化计算过程中,作者尝试过使用更大的迭代代数和种群数量、调整交叉和变异概率,但进一步的迭代修正并不能进一步缩小频率修正误差,其原因可能有以下两个方面:
1)模型修正时假定参数误差是有限元模型误差的最主要(唯一)因素,因而未能处理模型结构误差和模型阶次误差;
2)所选择的修正参数未包括所有可能的误差参数。
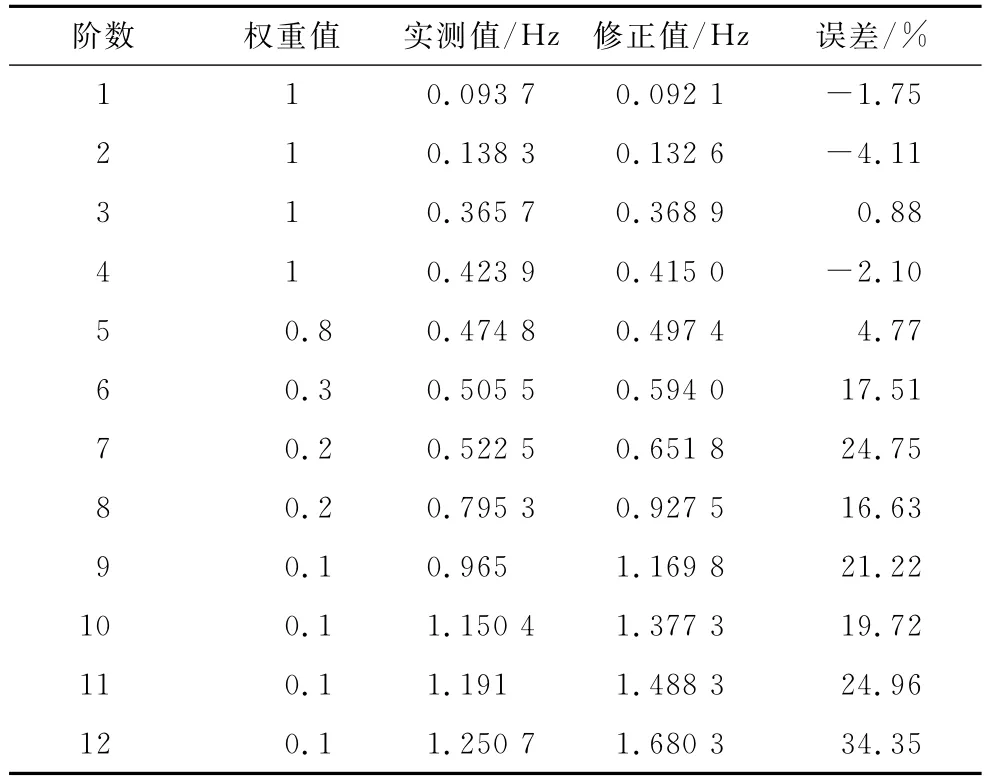
表5 修正后的频率值
4 结 语
通过本文的研究可得结论如下:
1)对于像广州新电视塔这样的超高层柔性钢结构,其基频为0.093 7Hz,且模态频率非常密集,要准确识别其模态参数,须运用2种以上的方法进行相互校对,同时工作者也须具备一定的工程经验。
2)本文运用的3种模态参数识别方法,其频率识别结果非常吻合,但阻尼比识别结果差异较大。再一次验证了大型工程结构的阻尼机制复杂,难以精确识别其阻尼比的问题。
3)结合遗传算法对GNTVT的初始有限元模型进行动力模型参数修正,虽然结果尚可接受,但优化迭代的过程需要花费很长的计算时间,且精度不是十分高。要想获得更精确的有限元模型,需全面考虑结构的参数误差、结构误差和模型阶次误差。
[1]张瑞云,曹双寅.结构模型修正的遗传算法方法研究[J].桥梁建设,2008,1:23-26.
[2]陈伟欢,吕中荣,陈树辉,等.高耸结构建造阶段环境振动测试与模态分析[J].中山大学学报:自然科学版,2010,49(5):34-40.
[3]GNTVT benchmark[DB/OL].http://www.cse.polyu.edu.hk/benchmark/index.htm.
[4]Ye X J,Yan Q S,Wang W F,et al.Modal identification of Canton Tower under uncertain environmental conditions[J].Smart Structures and Systems,2012;10(4/5):353-373.
[5]Faravelli L,Ubertini F,Fuggini C.Subspace Identification of the Guangzhou New TV Tower[C]//Proceedings of 5th World Conference on Structural Control and Monitoring,Tokyo:2010.
[6]何少宁.广州新电视塔竖向地震作用分析[D].西安:西安建筑科技大学,2006.
[7]李春林.高耸结构风振响应分析研究[D].广州:广州大学,2007.
[8]钟颖.基于静力测试数据的桥梁结构有限元模型修正[D].成都:西南交通大学,2009.
[9]梁文广.框架结构模型修正与损伤识别研究[D].重庆:重庆大学,2009.
[10]闫桂荣,段忠东,欧进萍.遗传算法在结构有限元模型修正中的应用[J].哈尔滨工业大学学报.2007,39(2):181-186.
