EE型松耦合变压器的精确磁路模型和仿真分析

张建伟，曹 彪

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

目前，电能主要是由导线通过插头插座直接接触进行能量传送。这种电能传输方式由于存在物理接触和电气接触，在诸如潮湿、易燃易爆等环境中的应用受到限制，而且可靠性差，影响美观，浪费大量的走线。新型感应供电系统综合运用电磁耦合技术、高频变换技术以及电力电子等技术，通过采用一、二次侧可分离的松耦合变压器将电能从电源侧经气隙传递给一个或多个用电系统[1-5]。

文中研究了电动汽车感应充电系统的关键装置松耦合变压器，通过分析磁路及横截面积对变压器的初次级绕组电感和耦合性能的影响，结合Ansoft有限元分析软件对松耦合过程进行了仿真和分析，得出EE型松耦合变压器精确磁路模型，并绕制了松耦合变压器，测量实际数据，对比实验效果。

1 感应充电技术简介

感应充电主要分为3类[1]，考虑电动汽车需要，文中选用第一类感应充电方式。结合文献[2]，在同等条件下，EE磁芯传输效率较高，成本相对较低，故文中选用EE磁芯进行设计。

电动汽车充电系统框图如图1所示，松耦合变压器左侧部分在地面，右侧部分在车体上，通过松耦合变压器实现能量的无接触传输。

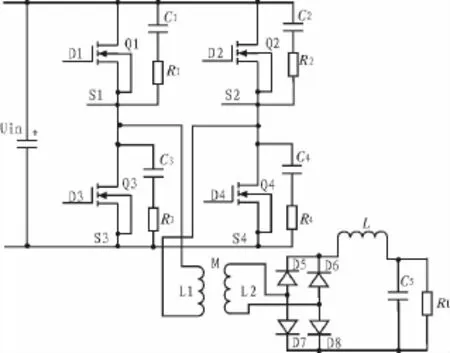
图1 电动汽车感应充电系统拓扑Fig.1 Topology of inductive charging system of EV

2 二维涡流场分析与参数测量

对于工程电磁场问题，当分析正弦激励源下的物理现象，如电机、变压器的涡流损耗计算，需要进行涡流分析。如果电磁装备具有对称性，常常将三维涡流场问题简化为二维问题进行分析[6-7]。

2.1 仿真模型

文中选用的是EE65磁芯，磁芯材料为铁氧体，工作频率为100 kHz，磁导率为2 000；线圈材料为铜，气隙为空气，边界为气球边界。构建二维模型如图2所示。初次级线圈匝数均为12匝20股并绕，采用叠绕方式[8]，每匝绕一层。初级线圈施加正弦电流，次级线圈施加电流为0，通过电磁感应可以将能量从初级传递到次级。然后求解，可以计算阻抗、磁感应强度、自感互感和耦合系数等。

图2 松耦合变压器二维模型Fig.2 2D model of loosely coupled transformer

在感应充电系统松耦合变压器中，主要参数有：初次级绕组位置、气隙大小、水平位移和工作频率等，前人通过这些参数对松耦合变压器的初次级绕组电感和耦合性能的影响已作了大量的研究，这里就不再赘述了。文中主要通过研究EE磁芯的磁路精确模型，并探讨通过改变磁芯横截面积来提高耦合系数，并实际测量，观测其输出波形。

2.2 简化磁路模型分析

根据图 2 模型，进行磁路分析[2，5，6]如图 3 所示，虚线为磁通分布，由磁路相关知识，知道磁路磁阻：

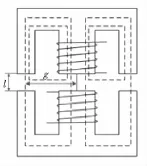
图3 磁通分布图Fig.3 Distribution of the magnetic flux

由于空气磁阻的磁导率系数远远小于铁氧体的磁导率系数，在计算时候忽略磁芯内部的磁阻，只考虑空气磁阻，所以图3经过等效磁阻电路分析，简化为图4所示。由于气隙大小一样，中心磁柱的面积为两侧磁柱的面积的两倍，在计算时，选取中心磁柱的空气磁阻为RE1时，则两磁芯磁柱的空气磁阻根据公式计算，知道为2RE1。

则磁动势为：

图4 磁路等效图Fig.4 Equivalent diagram of magnetic circuit

得到耦合系数为：

综上（2）（3）所述可得到：

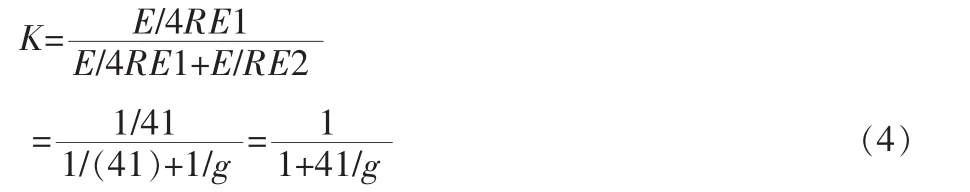
当气隙变大时，RE1增大，Ø1减小，耦合系数会变小；而增大中柱与侧边柱的距离，发现RE2增大，Ø2减小，从而耦合系数也会提高。实际情况，磁通不仅经过磁芯的端面，而且还会通过气隙的边缘、尖角、气隙附近的磁芯侧面流通（如图5所示），这些磁通通常称为边缘磁通。所以在实际计算时，想得到比较精确的结果，这些边缘磁通对整体的影响是不可忽略的。

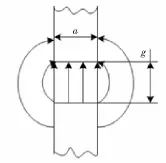
图5 边缘磁通Fig.5 Fringing magnetic flux

2.3 精确磁路模型分析

根据EE型松耦合变压器的仿真结果，如图6所示，在其磁芯周围会有边缘磁通出现。有限元以及磁场相似原则分析磁场虽然准确，但是使用的情况毕竟有限，比较好的方法是估计磁通的可能路径，把整个磁场分成几个区进行分析求解，并与磁路模型中的磁阻对应起来，虚线为划分的区域。

图6 磁力线分布和磁通分块示意图Fig.6 Separation of the magnetic flux and distribution of the magnetic field line

根据磁通的耦合程度，结合上述的磁场分布来定义非接触变压器的磁阻，进而得到EE型松耦合变压器磁阻等效磁路图，如图7所示。

图7 EE型非接触变压器精确磁路模型Fig.7 Magnetic reluctance circuit with better accuracy

对比图4，模型虽大体上是一致的，关键是磁阻的变化，结合公式（3），新的耦合系数表达式为：

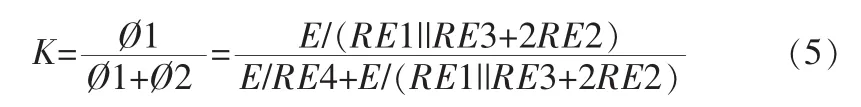
其中，为边柱的正对磁阻，为中心磁柱的正对磁阻，为边柱的边缘磁通，为漏磁通。

2.4 气隙磁阻的计算

根据建立的模型和实际的需要，气隙相对端面的尺寸较大，故结合图5和2.3所分析的结果，参照图9的矩形端面边缘气隙磁导的分布，把整个磁场分为几个简单的几何形状的磁通管[11－14]，然后用下列近似公式进行求解：

式中，Abav——磁通管道的平均截面积（m2）；lbav——磁通管内力线的平均长度（m）；Vb——磁通管体积（m3）。 整个气隙磁导是这些磁导的总和，然后根据磁导可以求解磁阻的大小。

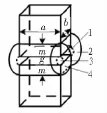
图8 矩形磁极之间的边缘磁导Fig.8 Fringing magnetic

根据图6划分的区域及图8的磁通管道的编号，将其磁导的计算值列入表1所示。然后根据实际的磁导分布及参数，计算总磁导，与图8的磁阻对应起来。

由于是矩形截面， 知道 f=（a－e）/2，m=g，L1=（e－d）/2，h 为线圈的高度，根据EE磁芯的实际情况，计算各个数值，各个参数如表2所示。

结合图6～图8和表1，计算各部分的磁阻，其中，边缘磁通由几个半圆柱、半圆筒和球组成；漏磁通由半椭圆柱和矩形组成。

得到精确模型的耦合系数，保留关于c的表达式，得到耦合系数的精确表达式。通过改变磁芯厚度，改变磁芯的横截面积，达到改变耦合系数的目的。

改变c的值，与Ansoft模拟的结果进行对比，如图9所示，厚度增加，耦合系数提高，但考虑磁芯并联的个数增加越多，磁芯的整体重量增加，但耦合系数提高不明显，所以最终权衡选用2个磁芯并联来增加面积。

表1 磁通管结构Tab.1 Flux tubes for the reluctances

表2 各距离取值Tab.2 Values of different distance

图9 耦合系数随面积改变Fig.9 Coupling coefficient with the area change

3 实 验

3.1 自感互感测量

根据互感模型[4，11－13]，测量松耦合变压器的自感和互感参数。一对异名端相联，另一对异名端与电路相接，这种连接方法称为顺接串联（顺串）；一对同名端相联，另一对同名端与电路相接，其连接方法称为反接串联（反串）。则计算正向总电压，最后获得等效电感为：

反向串联等效电感：

联立（8）（9）可以获得互感为：

本实验是借助LCR测试仪进行测量，将测量数据进行处理，可以得到对比结果。

3.2 变压器初次级参数测量

根据上面的分析结果和测量方式，改变气隙时，得到两种松耦合变压器的耦合系数变化曲线如图10所示，发现耦合系数平均能提高7.5%。

图10 耦合系数对比Fig.10 Contrast of coupling coefficient

其中 “耦合系数2”为双磁芯并联磁芯条件下测量的数据，“耦合系数1”为单个磁芯情况下测量的耦合系数。

搭建实验平台，在220 VAC的输入情况下，改变气隙大小，测量2个松耦合变压器的输出波形电压参数如图11所示。

图11 输出电压对比Fig.11 Contrast of output

其中，2输出为2个磁芯并联测量波形，1输出为一个磁芯测量波形，发现输出能力得到有效提高，在6 mm处输出能力最大提高40 V。

4 结 论

最终得到大气隙情况下的EE磁芯的精确磁路模型，并结合精简模型公式，得出横截面积对耦合系数的影响，并通过Ansoft仿真进行了验证，实验证明通过双磁芯并联来增加横截面积可以使耦合系数平均提高7.5%，并实际测量两个磁芯在相同的输入情况下，2个并联磁芯的输出能力明显较强，在气隙为6 mm处，输出能力最大提高40 V。

[1]赵小坤.电动汽车感应充电技术的研究[D].哈尔滨：哈尔滨工业大学，2009.

[2]严沁.感应耦合能量传输系统关键技术的研究 [D].上海：东华大学，2010.

[3]陈国东.非接触电能传输系统恒流技术研究 [D].重庆：重庆大学，2008.

[4]顾佳炜.非接触供电系统工程化关键技术及其应用研究[D].南京：南京航空航天大学，2011.

[5]王天宇.基于松耦合变压器的大功率感应电能传输技术研究[D].哈尔滨：哈尔滨工业大学，2010.

[6]刘国强，赵凌志，蒋继娅.Ansoft工程电磁场有限元分析[M].北京：电子工业出版社，2005.

[7]刘修泉，张炜，吴彦华，等.体内微机电无线能量传输系统的仿真分析[J].系统仿真学报，2008，20（8）:2215-2219.LIU Xiu-quan，ZHANG Wei，WU Yan-hua，et al.Simulation and analysis of loosely wireless power transmission of MEMS in human body[J].Journal of System Simulation，2008，20（8）:2215-2219.

[8]张旭.感应耦合式电能传输系统的理论与技术研究[D].徐州：中国矿业大学，2011.

[9]潘冬婷.无接触电能传输系统的设计与实现[D].大连：大连理工大学，2010.

[10]Li J Y，Shen H Y，Chang T W.Contactless inductive charging system with hysteresis loop control for small-sized household electrical appliances[J].IEEE，2012:2172-2178.

[11]蔡元宇.电路及磁路[M].北京：高等教育出版社，2000.

[12]电子变压器专业委员会.电子变压器手册[M].沈阳：辽宁科学技术出版社，2000.

[13]赵修科.实用电源技术手册：磁性元器件分册[M].沈阳：辽宁科学技术出版社，2002.

[14]张巍，陈乾宏，Wong S C，等.新型非接触变压器的磁路模型及其优化[J].中国电机工程学报，2010（9）：108-116.ZHANG Wei，CHEN Qian-hong，Wong S C，et al.Reluctance circuit and optimization of a novel contactless transformer[J].Proceedings of the CSEE，2010（9）：108-116.