国内外悬垂绝缘子串风偏设计参数对比与分析
2013-08-10闵绚邵瑰玮文志科蔡焕青胡霁曾云飞
闵绚,邵瑰玮,文志科,蔡焕青,胡霁,曾云飞
(中国电力科学研究院,武汉市 430074)
0 引言
输电线路的风偏闪络事故一直是电网正常运行的重大安全隐患之一。输电线路一旦发生风偏跳闸,造成线路非计划停运的几率较高,严重影响供电可靠性,造成巨大的经济损失。
据统计,国家电网公司系统2007—2011年间,各年66 kV及以上输电线路因风偏分别发生跳闸157、93、79、174、85 次,跳闸率分别为 0.0346、0.0185、0.0143、0.029、0.014 次/(100 km·a);引起线路故障停运分别为83、56、32、69、32 次,重合成功率分别为 47.1%、39.8%、59.5%、60.3%、62.4%,涉及江苏、浙江、安徽、湖北、河南、山东、山西、北京、福建等省市。
调研表明,美国和日本等发达国家输电线路较少发生风偏放电[1-6]。对比国内外相关绝缘子串风偏设计资料可以发现,国内外在风偏角计算模型及方法上基本是一致的,即都是按照刚体静力学模型来计算;但是在悬垂绝缘子串风偏设计中有关基本风速、风压不均匀系数、风压高度变化系数等参数的选取上存在着不同。
1 基本风速
风是由大气中气团的运动而形成的,其运动过程受路径上各种障碍物,如高山、河流、湖泊、海洋、树木、房屋、建筑物等的影响,因此,在接近地表处,风速和风向显得较为紊乱,通常将接近地表的流动风称为近地面层风(简称为近地风)。在增加到一定高度以后,不同地貌特征下的风速趋近于相等,该高度称为梯度风高度。随着地表特征的不同,梯度风高度一般为300~500 m。
在近地风范围内,随着距地面高度的不同,风速是逐渐变化的。一般认为,在一定时间间隔内,给定位置上风速的平均值几乎不变,但随着距地面高度的增加而增大。在不同的地貌特征条件下,风速随水平高度变化的规律不同;在相同地貌特征条件下,随着周围环境的变化,同一水平面高度但不同位置的风速和风向也不同。
因此,实际工程中为确定设计风速的大小,首先根据工程所在地的气象观测数据,按照一定方法换算至标准条件下的风速(基本风速)。不同的工程类型,对于标准条件的规定不尽一致。对于架空输电线路,GB 50545—2010《110 kV ~750 kV架空输电线路设计规范》规定:“确定基本风速时,应按当地气象台、站10 min时距平均的年最大风速为样本,并宜采用极值Ⅰ型分布作为概率模型,统计风速的高度应符合下列规定:110 kV~750 kV输电线路统计风速应取离地面10 m;各级电压大跨越统计风速应取离历年大风季节平均最低水位10 m。”[7]
由以上分析可见,输电线路设计基本风速的确定涉及到统计样本选取、风速次时换算、设计重现期考虑、风速概率模型选择等。
1.1 统计样本选取
在同一地点,越靠近地面,近地风遇到障碍物越多,风能量损失越大,但离地越高,地面障碍物对风的影响越小,相应风速随着高度的增加而增大。由于我国气象台风速仪安装高度大多为8~12 m,我国GB 50545—2010规定统计风速的高度为:(1)110~750 kV输电线路统计风速应取离地面10 m;(2)各级电压大跨越统计风速应取离历年大风季节平均最低水位10 m。世界上规定10 m为标准高度的占大多数,例如美国、俄罗斯、加拿大、澳大利亚、丹麦等国,日本采用离地15 m高为标准高度,瑞士为5~20 m,挪威、巴西为20 m等。虽然上述国家规定的标准高度不同,但是不同高度处的风压是可以根据风压高度变化系数进行换算的,在技术操作上没有影响。
确定输电线路设计风速需要依据长期观测的风场数据,当发现气象台站的观测数据不连续,表现为分段的系统性偏大或偏小时,要通过了解气象台站建站沿革,如气象台站周围环境的开发、设备使用情况、迁站与否等来查找和分析风速资料不连续的原因和确定处理方法。此外,由于输电线路多数远离城镇,甚至位于荒僻山岭,使得气象台站的观测数据不能完全覆盖线路走廊,因此需要对工程地进行大风调查,补充和完善线路风速的设计资料。
1.2 风速次时换算
在风速次时换算上,国内多是将定时观测风速(气象台、站一天定时观测4次的2 min平均风速)经过观测时距和次数的二重订正,换算为连续自记10 min平均风速。所谓的“时距”指求取平均风速时的时间间隔,其取值与换算后得到的平均风速大小有着密切关系。由于风速在时空分布上的不均匀性,一般而言,时距取值愈大,得到的平均风速愈小。根据美国气象局资料,在一个地面崎岖度均匀和梯度风不变的地区,最大1 min平均风速一般较最大5 min平均风速高约10%;日本观测结果为:以3~5 s平均时间为基础的瞬间最大风速为最大10 min平均风速的1.35~1.45倍(该比值被称为阵风系数);对于盆地和大城市,该比值可能会更大;而在海岸、草原和田野,有所减小[8]。
在风速观测次数方面,年最大风速有连续自记和定时观测之分。1953年前我国由于观测仪器不统一,每日观测有3、8、24次等;观测时距也不统一,有1、2 min。至1969年,全国各气象台站普遍使用维尔达风压板测风仪,观测时距逐渐统一为每日4次,每次记录2 min时距的平均风速。1969年后,自记风向风速仪(如达因式风向风速计)陆续装备各气象台站,开始积累连续自记风速资料,包括大风(>17 m/s)天气天数。以一天定时观测4次为例,其观测时间均匀分布在1天24 h内(如02:00,08:00,14:00,20:00),每天总共观测 8 min,因此有可能遗漏很多大风观测记录,设计前须将气象台站风速资料进行观测次数和风速时距换算,统一订正至GB 50009—2001《建筑结构荷载规范》(简称《结构规范》)所要求的连续自记10 min平均风速[9-11]。
此时换算公式为

式中:V10min为10 min平均最大风速,m/s;VTmin为定时2 min平均或瞬时最大风速,m/s;a、b为系数,可通过搜集当地分析成果或根据资料计算确定。
通过查阅资料得到国内各地区各时距平均风速之间的关系分别如图1、2所示。
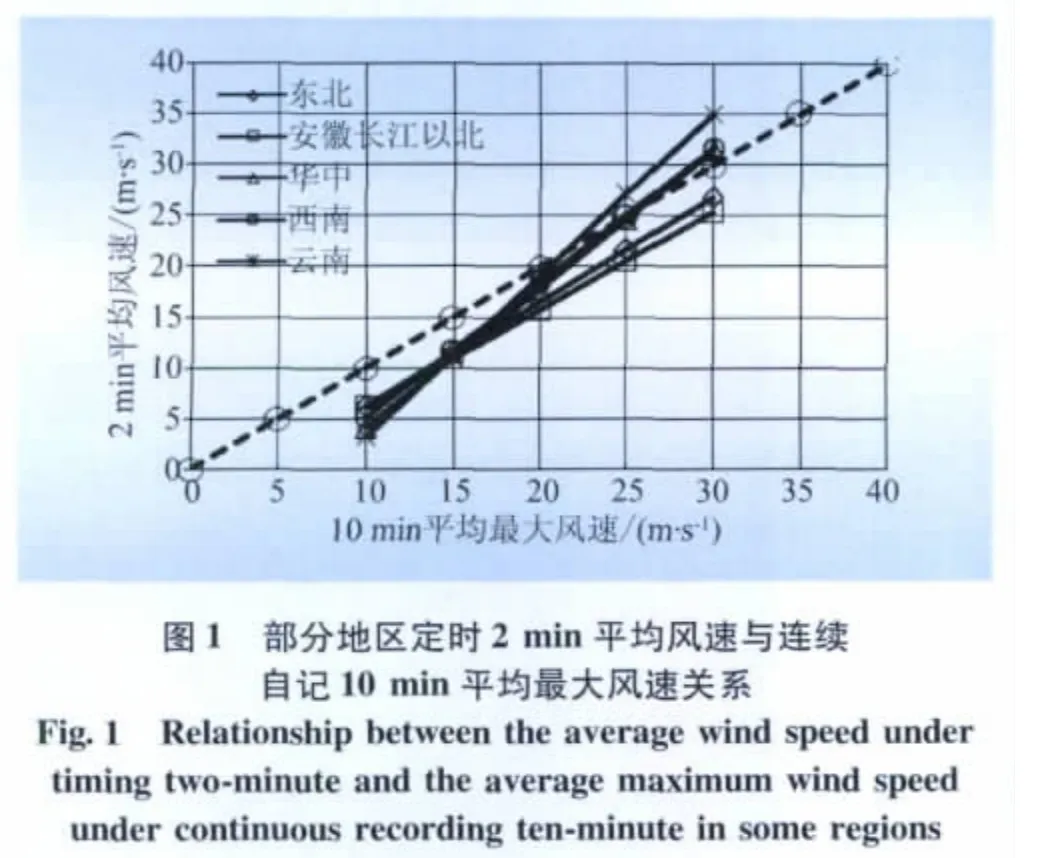

由图1可见,对于多数地区,当观测到的2 min平均风速较小时,换算得到的连续自记10 min平均风速值较定时观测的高,这反映了每日4次定时的短时距观测有可能遗漏大风的观测记录。随着观测到的2 min平均风速值提高,换算后的连续自记10 min平均风速值较定时观测的低,反映了由于风速在时空分布上是不均匀的,随着统计时距的增加,平均风速值逐渐降低。
由图2可见,瞬时最大风速总是较连续自记10 min平均风速高,且随着观测到风速的增高,二者之间的差异增加。当连续自记10 min平均最大风速为30 m/s时,我国各地区瞬时风速均约为45 m/s,约为前者的1.5倍,与日本的观测结果相吻合。
鉴于导线在大风下发生风偏的运动响应时间较短,在短时间的大风作用下线路即有可能发生风偏放电,而目前国内绝缘子串风偏计算方法并没有考虑短时大风的影响因素,设计中均采用时距较长的10 min平均最大风速,有可能使得在某些微地形、微气象区的线路防风偏安全裕度不高。
1.3 设计重现期与风速概率模型
一般我们所研究的对象不会出现异常风的气候,称为良态气候,对于这种气候,可认为年最大风速的每一个数据都对风极值的概率特性起作用。目前,世界上许多国家以年最大风速资料作为概率统计样本,再根据重现期要求由风速概率分布模型计算最大设计风速(或基本风速)。
重现期定义:大于等于或小于等于某一水平的随机事件在较长时期内重复出现的平均时间间隔,常以多少年一遇表达。重现期(T,年)与频率(P)的关系为T=1/P,例如:当P=1%时,则T=100年,称为百年一遇。所谓百年一遇是指大于或等于某一水平的事件在很长时期内平均百年出现1次,而不能理解为恰好每隔100年出现1次。对于具体的100年来说,超过该水平的事件可能发生不止1次,也可能1次都不出现,但在长时期内平均每年出现1次的可能性为1%。
国际输电线路通用标准IEC 60826中规定了线路设计的安全等级,最低不得低于1级;230 kV及以上电压等级的一般线路应为2级;高于230 kV电压等级,且为电网主干或者供给特殊负荷的唯一电源线路,应为3级。各安全水平等级线路风荷载重现期分别对应 50、150、500 年[12]。
美国《输电线路结构荷载导则》根据线路重要性程度,规定其可靠性水平分别取为100、200、400年一遇;对于临时线路,规定其重现期可小于50年一遇,但一般取50年一遇[13]。
2002年,我国建设部发布了《结构规范》[10],把风荷载的重现期由30年一遇提高到50年一遇,对于高层建筑、高耸结构以及对风荷载比较敏感的其他结构,基本风压可适当提高。我国GB 50545—2010参考现行国家标准《结构规范》,将500~750 kV输电线路(含大跨越)的重现期定为50年,110~330 kV输电线路(含大跨越)的重现期定为30年。由于特高压线路的重要性,GB 50665—2011《1000kV架空输电线路设计规范》(简称《1000kV设计规范》)规定其基本风速数理统计重现期取100年[14],如表 1所示。

表1 我国各电压等级输电线路设计重现期规定Tab.1 Design return period of transmission lines with different voltage levels in China
关于年最大风速概率分布模型方面,通常有极值Ⅰ型、极值Ⅱ型、韦布尔分布模型和经验频率法等。目前多数国家(包括中国、加拿大、美国和欧洲钢结构协会等)采用极值Ⅰ型概率分布函数。
表2为我国某沿海城市1989—1998年间各年最大风速统计资料(B类地区,已换算至距地面10 m高度处连续自记10 min平均风速)。

表2 某沿海城市的年最大平均风速表Tab.2 Annual maximum average wind speed in a coastal city
以极值I型概率分布为例,计算得到该地区不同重现期下年最大风速(即线路设计中基本风速)以及所对应的基本风压如表3所示。

表3 不同重现期下的基本风速Tab.3 Basic wind speed in different return periods
由表3可见,重现期为50年一遇对应的基本风速值较30年一遇提高了约5.3%,风压则增加了10.3%左右;重现期为100年一遇对应的基本风速值较50年一遇提高了约5.3%,风压则增加了10.3%左右;当重现期增大到500年时,其对应的基本风速值较30年一遇提高了约29.0%,风压则增加了66.7%左右。
2 风压不均匀系数
关于导线风荷载(风压),考虑到风速在空间分布上的不均匀性和时间上的强度变化,线路设计规范中引入了风压不均匀系数(α),以对整档导线在大风下的实际受力进行计算。风压不均匀系数的定义为:“沿整个档距导线所承受的风速,不可能在各点上同时都一样大。因此,作用在导线上的合成风压将不由最大风来确定,而由其平均值确定。为使选用的风速值与整个档距中导线受风情况相吻合,应考虑一个降低系数,该系数即为风压不均匀系数”。由此可见,风压不均匀系数α与风速和档距有关。目前,国内外对其取值规定不尽相同。
日本JEAC 6001—1999《架空送电规程》第4章第6节第6-2条规定:在计算导线风压时应乘以构造规模降低系数(即风压不均匀系数),其计算公式[15]为

式中s为档距长,m。
同时该条文还规定,当导线风偏计算采用简化算法时,对于200 m以上的档距,β一律取为0.7。
德国按照欧洲标准《高于45 kV的架空交流电力线路第一部分:一般条件和规范》(EN 50341—1:2001)的《德国国家标准解译》(NNA)中的条款,在新设计架空送电线路时,导线风压和风偏计算按以下公式[15]:
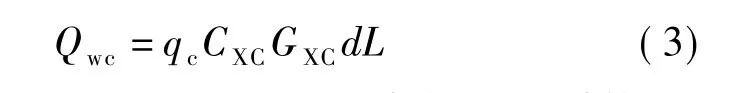
式中:qc为单位风压,N/m2;CXC为空气阻尼系数(相当于我国规程中的导线体型系数);GXC为导线响应系数(即风压不均匀系数),当L<200 m时,取0.75,当L>200 m时,取0.45+60/L;d为导线直径,m;L为水平档距,m。
我国在风压不均匀系数的选取上,考虑到由于风速空间分布的不均匀性,设计规范中引入了风压不均匀系数对整档导线的风荷载进行折算。在该参数的选取上,20世纪80年代初期,投运的500kV输电线路风压不均匀系数是按照0.75来计算导线风偏角的。20世纪80年代后期,根据德国的设计规范和我国东北某试验场2年的试验观测数据,当风速≥20 m/s时,DL/T 5092—1999《110~500kV 架空送电线路设计技术规程》中将该系数从0.75修改为0.61[16]。20世纪90年代中期,我国投运的500kV输电线路风压不均匀系数多是按照0.61来设计风偏角的。
20世纪90年代中期以后,特别是2004年入夏后的短时间内,国家电网公司所辖的500kV架空送电线路发生风偏闪络21次,呈高发态势。尽管随后展开的调查并没有确切的证据表明风压不均匀系数取值不当,但作为应急措施,国家电网公司建运部决定在架空送电线路设计中按照“风压不均匀系数取值0.61进行设计,按0.75进行校核”。
现阶段,我国颁布的 GB 50665—2011和 GB 50545—2010中在导线风偏角设计时仍然仅按设计风速来选取风压不均匀系数。但规定在校核时,需要考虑档距的影响。档距小于200 m取0.8,档距大于550 m时取0.61,档距在200~550 m之间风压不均匀系数采用式(4)计算。
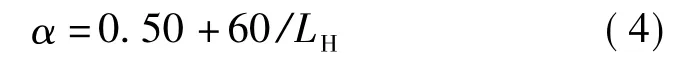
式中LH为水平档距,m。
不同国家风压不均匀系数取值对照如表4所示,由表4可得:与其他国家的α取值方法相比,我国设计规范规定的α取定值0.61,覆盖的风速范围宽,适用于所有的档距。在小档距范围内α仍取0.61,明显低于其他国家规程的取值,例如:在档距为300 m时,日、德规程的α取值分别为0.63和0.65,均大于我国的0.61取值。
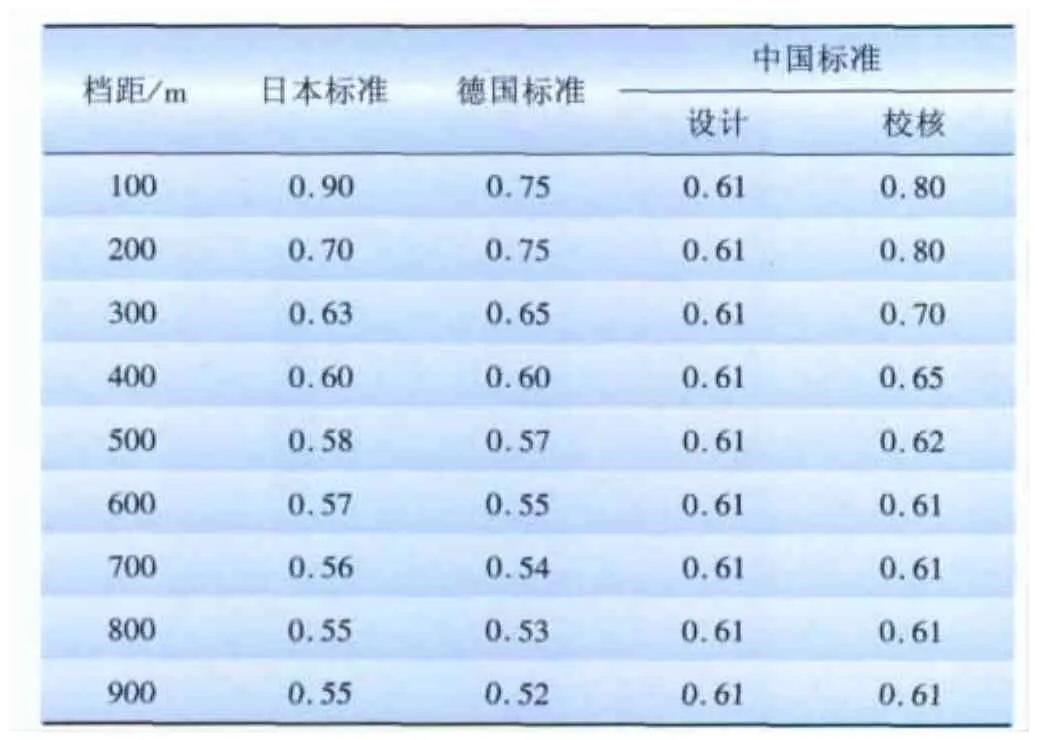
表4 不同国家风压不均匀系数α取值对照Tab.4 Values of α in different countries
此外,通过研究发现:风压不均匀系数折算方法对导线悬挂点处风荷载的大小也有影响,具体建模方法见文献[17]。根据风压不均匀系数的定义可知,实际作用于导线上的风压并不是沿导线均匀分布的,而是可能集中作用于整档导线的某一段上,其示意图如图3、4所示,图中w0为风压,L和L'为档距。
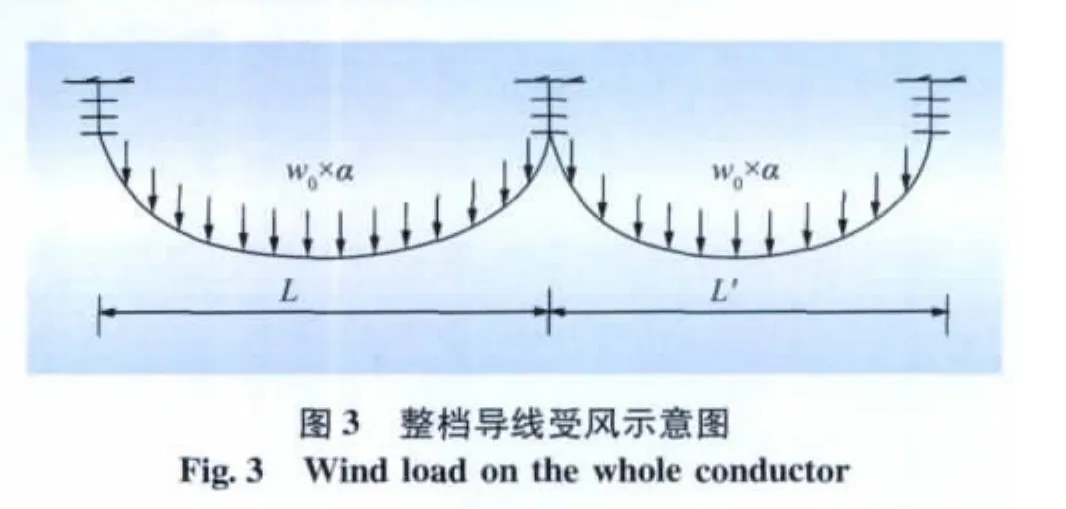

比较图3、4可见,2种计算条件下整档导线所受总风荷载相同,但风荷载的作用位置发生了变化,这对等效作用在绝缘子串最下端的水平荷载大小有明显影响。以500kV线路为例,计算条件为:悬垂绝缘子串为28片XP-16,导线型号为4×JL/G1A-400/35,水平档距为500 m,高差为0 m,导线高度处的风速为30 m/s,风向与导线轴向夹角为90°,风向与水平面夹角为0°。通过有限元软件仿真得出:当风集中作用在绝缘子串最下端附近时,风荷载的差异率随风压不均匀系数取值变大逐渐变小,如:风压不均匀系数为0.6时,仿真计算得出的导线悬挂点处风荷载比设计规范给出的大38.69%。说明由设计规范计算得出的水平风荷载与风集中作用在绝缘子串最下端附近时得出的值区别明显,所以,在线路的实际运行中,即使导线高度处的实际风速没有超过其设计风速,线路仍有可能会发生风偏跳闸。
3 风压高度变化系数
在大气边界层中,越接近于地面,风速越小,只有在300~500 m以上的高度,风速才不受地面粗糙度的影响而可以自由流动,达到所谓的梯度风速。在大气边界层中,风速沿高度的变化规律称为风剖面,我国规范采用指数型的风剖面:

式中:a为地面粗糙度指数;z0为基准高度,我国规范取作10 m;z为任一高度或离地高度,m。为高度z处对应的平均风速,m/s;为标准参考高度zb对应的平均风速,m/s。
不同的地面粗糙度类别,其地面粗糙度指数是不一样的,达到“梯度风速”的高度也不相同,这反映了在不同的地面粗糙度类别下,其风剖面也不一样。一般地,地面越是光滑,其所需梯度风速高度较低,指数a较小;反之,地面越是粗糙,梯度风高度越高,指数a越大。
不同国家的规范针对本国的实际地面粗糙度类别规定了相应的a,表5列出了在不同地形条件下中、美、日3个国家的a取值[18-19]。我国规范规定标准地面粗糙度类别为比较空旷平坦地面,指田野、乡村丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区,即B类地面粗糙度类别。
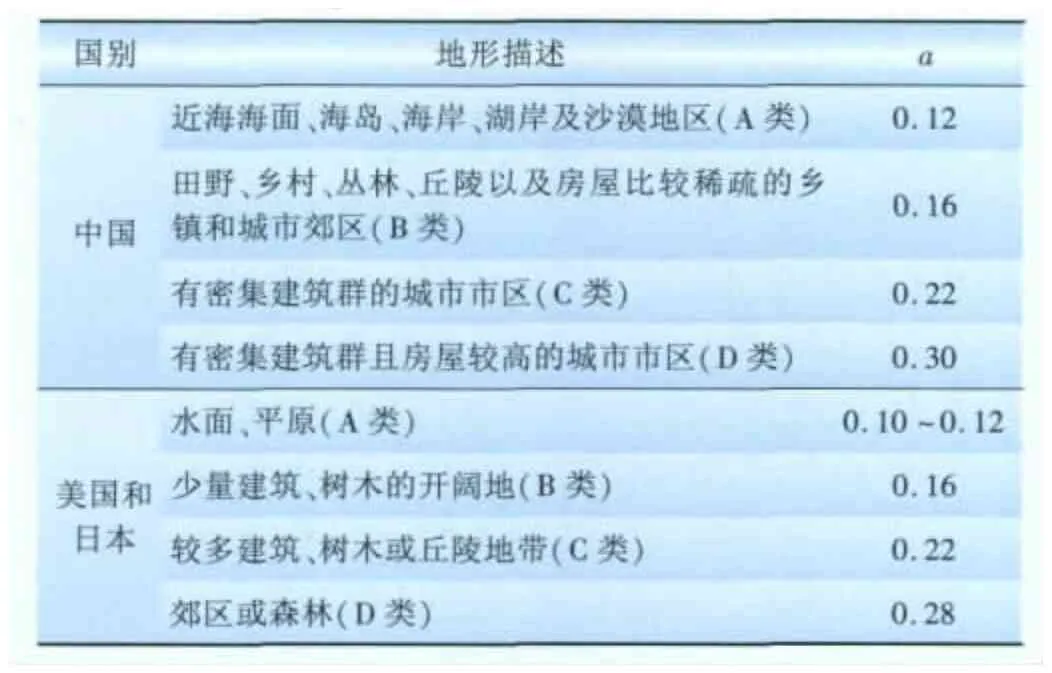
表5 不同地形条件下中、美、日国家的a取值Tab.5 Selecting of a in China,America and Japan under different terrains
以1000kV特高压线路为例,基本风速为30 m/s,水平档距和垂直档距为600 m,风向与导线轴向夹角为90°,风向与水平面夹角为0°,风压不均匀系数为0.61,绝缘子串为54片XWP-300,导线型号为8×JL/G1A-500/35。改变地形条件,计算得到的绝缘子串摇摆角如图5所示。

图5 不同地形条件下的风偏角Fig.5 Windage angles on different terrains
由图5可得,与B类地区的风偏角相比,A类、C类和D类与其风偏角的差异率分别为6.63%、-10.48%和-25.67%,不同的地形条件对风偏角的影响较大。
此外,不同的地面粗糙度有不同的风剖面,当风进入新的风剖面中时,在达到平衡状态前,必须经过某一地面距离,称为过渡区,随着风行程的增加,新的风剖面将逐步形成。风速随地面粗糙度类型的改变如图6所示,当上游风从一个地面粗糙度进入另一个地面粗糙度类别时,沿风的行程x将有一个内边界发展高度,并随距离x的增加,逐步将流动调整为不连续下游区新的地面粗糙度指数a。内边界层发展高度hi随距离xi的关系为

式中:hi为内边界层发展高度,m;xi为下风距离,m;z0为地面粗糙度长度。

图6 内边界层发展高度Fig.6 Developing height of internal boundary layer
调研资料表明[20-21],在新地面粗糙度改变点开始的下游xi或500 m距离内,风速剖面线仍与不连续上游的风速剖面线相同;但对于完成形成下游区地面的最小距离,英国规范[22]认为需要1 km或更长的行程,或根据地面上房屋和其他障碍物的密集程度采用所需的最小行程;而澳大利亚规范则规定了平均风所需的行程为x-xi≥1.5 km或50 H(H为结构高度)的大者,可以完全形成新的地面粗糙度。而在这个范围之内,则属于过渡区。在过渡区的上层,将受到上游地面粗糙度的影响,而在过渡区的下层,将受到下游地面粗糙度的影响,在上、下层之间,还有一段上、下游联合影响的区域,如图7所示。
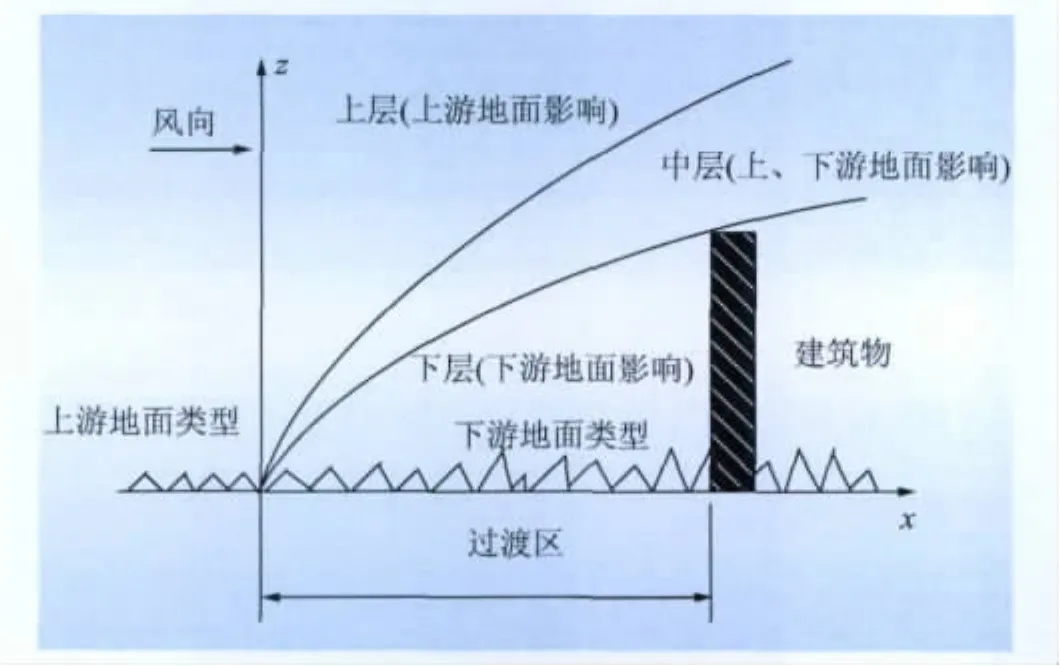
图7 上、下游联合影响区域Fig.7 Influence regions between upstream and downstream
当地面粗糙度改变时,依据结构所处的不同位置,其风速将有所不同。依据澳大利亚规范[23],则:
(1)当结构所处位置x<xi时,仍取上游地面类型下的风速和风压;
(2)当结构所处位置x-xi≥1.5 km或 x-xi≥50 H(取大者)时,取下游新的地面类型下的风速和风压;
(3)当结构所处位置0<x-xi<1.5 km(50 H)时,新的下游地面的风速应进行修正。
但是我国的线路设计规范并没有对上述过渡区地面粗糙度类别的选取进行明确的定义,往往将这类地形归属到微地形区、微气象区,给线路的防风偏设计带来了一定的困难。
综上所述,在导线对地高度不变时,不同的地面粗糙度类别对风压高度变化系数的取值影响较大,且我国线路设计规范只规定了平坦或稍有起伏地形的风压高度变化系数取值,对于微地形区(如:过渡区、丘陵、山脊等)如何来划分风压高度变化系数取值并没有进行明确的定义。此外,风压高度变化系数仅是针对较长时间的平均风风压换算,对于瞬时风的风压换算,其是否适用还有待进一步的研究和分析。
4 结论
(1)在基本风速方面,国外无论是在风速次时换算时间段还是重现期的选取上均与我国存在较大差异。
(2)在风压不均匀系数的选取上,日本和德国是按照不同档距来选取该系数,而我国规范中在导线风偏角设计时仍然仅按设计风速来选取风压不均匀系数。规定在校核时,需要考虑档距的影响,但是当档距超过600 m时,风压不均匀系数仍取定值0.61;且风压不均匀系数折算方法对导线风荷载的影响显著,当风集中作用在绝缘子串最下端附近,风压不均匀系数为0.6时,仿真计算得到的风荷载比设计规范给出的大38.69%。
(3)在导线对地高度不变时,不同的地面粗糙度类别对风压高度变化系数的取值影响较大,我国的线路设计规范没有对过渡区地面粗糙度类别的选取进行明确的定义,往往将这类地形归属到微地形区、微气象区,给线路的防风偏设计带来了一定的困难。
(4)目前风偏设计参数的取值并不能完全满足我国输电线路防风偏的精细化设计需求,因此还需对不同地形特征下不同高度处的风参数进行现场观测,通过积累长期的观测数据,对上述这些设计参数取值进行优化和完善。
[1]刘焕明.500kV侯临线286号风偏故障分析[J].山西电力,2004(6):14-15.
[2]龚坚刚.浙江电网跳线风偏跳闸的分析与措施[J].华东电力,2007,35(5):112-114.
[3]牛彬,陈江华,姚俊峰.输电线路的风偏角问题分析[J].山西电力,2009(3):60-62.
[4]吴正树.500kV输电线路风偏闪络分析[J].广西电力,2009(1):29-43.
[5]韩锐.220 kV输电线路大转角耐张塔跳线风偏跳闸故障的反事故措施[J].安徽电力,2007(12):14-15.
[6]黄俊杰,汪涛,朱昌成.220 kV输电线路风偏跳闸的分析研究[J].湖北电力,2012(4):65-67.
[7]GB 50545—2010110 kV~750 kV架空输电线路设计规范[S].
[8]邵瑰玮,耿翠英,胡毅.国内外输电线路风偏设计参数比较与分析[J].高电压技术,2009,35(12):3106-3110.
[9]DL/T 5158—2002电力工程气象勘测技术规程[S].
[10]GB 50009—2001建筑结构荷载规范[S].
[11]东北电力设计院.电力工程高压送电线路设计手册[M].北京:水利电力出版社,1992.
[12]IEC 60826—2003 Design Criteria of Overhead Transmission Lines[S].
[13]ASCE 74—2009 GuidelinesforE1ectricalTransmission Line Structural Loading[S].
[14]GB 50665—20111000kV架空输电线路设计规范[S].
[15]徐小东,王钢.关于风压不均匀系数的研究[J].电力建设,2007,28(7):1-4.
[16]DL/T 5092—1999110 kV~500kV架空送电线路设计技术规程[S].
[17]邵瑰玮,闵绚,董彦武,等.输电导线悬挂点处等效风荷载仿真分析[J].高电压技术,2012,38(2):476-482.
[18]王永华.中美规范风荷载的计算比较[J].电力勘测设计,2012(1):67-70.
[19]侯小玲.建筑结构基本风速和基本风压问题浅析[J].山西建筑,2010,36(3):92-93.
[20]Bietry J,Simiu E.Mean Wind Profile and Changes of Terrain Roughness[J].J. Struct. Div.,ASCE(ST),1978(104):1585-1593.
[21]ANSI/ASCE7—2002 American Society of Civil Engineerings(ASCE).Minimum Design Loads for Building and other Structure[S].
[22]英国《规范》.建筑设计荷载(1984)[R]//《建筑结构荷载规范》管理组.外国建筑结构荷载规范汇编.北京:中国建筑科学研究院,1991:113-186.
[23]AS/NZS1170.2—2002 Australian Standard SAA Loading Code,Part 2:Wind Loads[S].
