实现水声定位浮标位置参数精确修正方法研究＊

赵 珩 李 斌

（91388部队94分队 湛江 524022）

1 引言

水声定位浮标是长基线导航定位系统对水下目标进行定位测量的基本测量单元，浮标位置数据的精确性对整个系统的定位精度有着直接的影响。由于水面工况条件复杂多变，使得浮标单元位置的不确定性增大，由此带来的误差因素也会增多，势必对其系统定位精度造成影响。对此，提出了针对海流不同、浮标姿态变化不同的修正方法，通过对修正前后的定位精度进行仿真对比，证明方法可行，海试证明可大大提高系统定位精度。

2 定位原理

采用无线水声测量浮标作为测量基本单元的长基线系统的基本工作原理是，在海面布设无线电浮标基阵，被测目标上加装的声信标周期性地发射声信号，各阵元浮标的水听器收到声信号，测得单程声传播时延，连同该时刻阵元的GPS位置数据打包，通过无线电上传至阵外船载数据处理中心。船载数据处理中心通过修正后的时延值与声速的乘积即可确定目标到各阵元之间的距离，从而得到空间球面交汇方程组，求解得出目标所处的位置，逐点定位解算得到目标的运动轨迹，由此为水下目标跟踪定位。工作原理如图1所示。

假设在测量海区布设N个浮标阵元，水下目标以航速v航行并周期性地发射声信号，浮标通过测量声信号的传播时间来实现对目标的定位的。每一组时间测量确定声源所在的一个球面，即：

其中（xi，yi，zi）和ti分别是第i个阵元的空间位置和第i个阵元接收到信号时刻相对于接收机时钟的时间，（xs，ys，zs）和ts分别为声源（目标）空间坐标和信号发射时刻相对于接收机时钟的时间，c为声波在水中的传播速度。

图1 工作原理图

对于同步式定位系统，声源、发射信号和接收机时钟同步，即ts＝0。这时式（1）的模型变成如下形式：

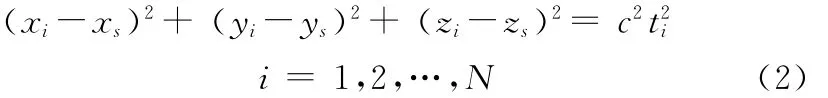
其中只有（xs，ys，zs）为未知量，其余均为已知量。显然，式（2）的模型是个“球面交汇模型”。众所周知，两个球面相交成一圆，三个球面相交于两点，一般来讲，四个球面相交即可确定出空间的一个唯一点。这就是同步式水声定位系统的基本原理。

当目标深度zs先验已知时，式（2）的“球面交汇模型”蜕化为“圆交汇模型”。两个圆相交于两点（相切时为一点），若有第三个圆方程，即可确定平面上一个唯一点，也就是说有三个时延值就能定出唯一的目标平面位置。

3 修正方法

3.1 误差因素分析

由于浮标半潜半浮的姿态，随水面工况条件变化不确定性大，对阵元位置数据的准确性造成影响，导致实时定位测量数据造成偏差。

GPS接收数据在定位解算中作为真值数据，故排除GPS本身的定位误差影响，浮标阵元的位置误差主要有以下两个因素造成（如图2所示）。

1）浮标姿态的不确定性导致和实时的GPS位置数据存在偏差。声速梯度不同，使得海面和海水中的水流不同，这势必导致浮标的姿态不固定，虽然可以通过将浮标锚底的方法解决其位置的漂移，但浮标原地的随波晃动使得所接收到得GPS实时数据和浮标重心还是会存在一个瞬时的偏角α；

2）水听器被水流冲击偏离实际GPS位置。一般来说接近海面的地方海流作用比较明显，由于浮标水下接收单元与水听器之间为电缆软连接，虽然通过在水听器上悬挂一定重量的方法，可以在一定程度上减小水听器的偏角θ，但是由于电缆本身的长度、韧性，使得水听器配重有限制，故水听器和浮标重心之间存在偏差d，而且电缆越长，偏差越大。

3.2 修正方法

1）浮标实时姿态修正

对浮标实时姿态的修正，可以在浮标上加装姿态测量传感器，通过软件对姿态传感器测量的航向β，纵倾γ和横摇φ进行如下转换：

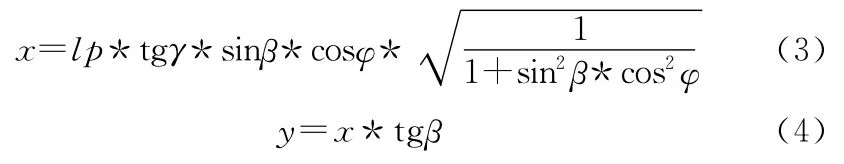
图2 浮标姿态示意图

得到浮标天线位置瞬时偏差，对GPS记录的当前位置数据进行修正，得到浮标重心处的位置数据。

此方法可以有效消除因浮标姿态不确定造成的偏差，使长基线定位系统的精度提升一个高度，但是大量加装姿态传感器会增加系统研制和维护的成本。

2）阵元位置偏差修正

假设为理想海区，流速和流向恒定，根据能量守恒定律，流速可用式（5）来计算，lp为电缆长度（假设为30m），θ为水听器随流偏角，h为水听器实际深度，为水听器水平位置偏差。

反推式（5），通过测得的流速V和流向δ，可以得到水听器偏角θ，用式（6）和式（7）可分别得到d和h，此方法可以修正阵元位置偏差，从而提高定位精度的可靠性。表1反映了水听器偏角、位置偏差、实际深度和流速的对应关系。

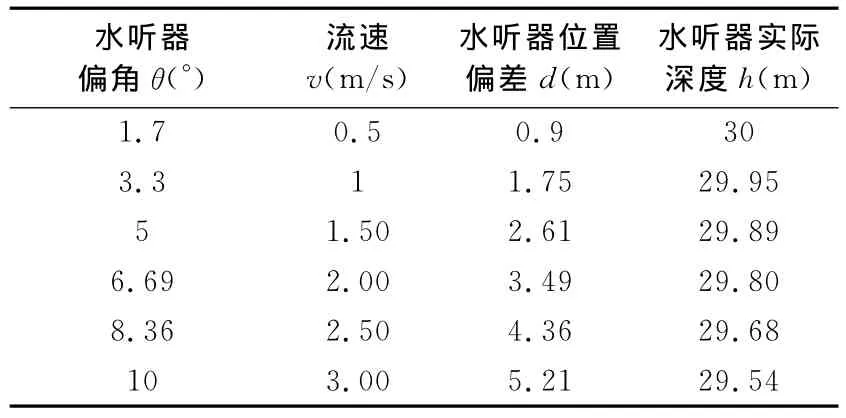
表1 水听器偏角、位置偏差、实际深度和流速的对应关系

4 仿真分析验证与测量数据验证

4.1 误差仿真分析

表2 浮标姿态及水听器偏差对定位精度影响的仿真分析

图3 误差分析图

从表2和图3中数据我们可以发现水听器位置随流偏差对系统定位精度影响是浮标的姿态偏差影响的5倍左右，分析原因可能是浮标水面以上部分长度有限，大约为4m左右，而水听器通过电缆软连接，电缆长度几十米，所以即使偏移相同的角度，水下部分比水上部分的距离偏差都要大很多。

表中后四组数据表示两种因素共同作用的效果，假设同一海区，理论流速流向恒定，水听器受流速影响偏角恒定，水听器偏向与流向一致，浮标倒向随波起伏不定，阵元瞬时位置数据的最大偏差为浮标倒向与流向相反，最小偏差为浮标倒向与流向相同。

我们以典型的长基线4km×4km的4元阵为例，对该系统在已知深度条件下的同步定位算法进行相应误差条件下的定位精度仿真。结合所分析的两个因素，在某一时刻上，阵元水听器和GPS天线之间都会和浮标重心有偏差，这必定对实际的定位解算数据造成误差影响。表2中我们假定海区流向、流速为恒定量，浮标的姿态倒向偏角随机，分别对浮标姿态和水听器随流偏向两种情况进行仿真。其中浮标倒向角度β为水平面夹角，浮标偏角α为垂直面夹角。

4.2 修正方法仿真验证

设置如表3所示的仿真参数，对修正方法进行仿真验证，仿真结果如图4和表4所示。

表3 仿真参数表

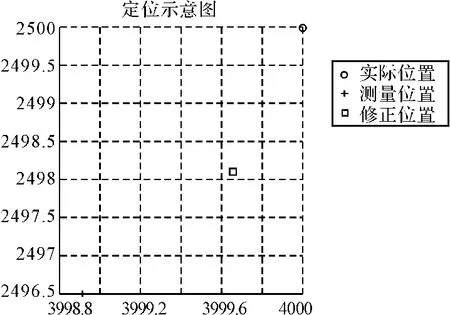
图4 定位仿真分析图

表4 定点测量数据修正精度仿真对比

从图表中可以明显比较出，修正后的定位精度远远高于未修正的精度，从理论上验证了该修正方法的可行性。

4.3 对测量轨迹数据进行修正对比

利用修正方法结合当时测量海域的水文数据，对一条测量轨迹进行修正验证。如图5所示，“·”状轨迹为浮标长基线测量系统测量轨迹，“－”状轨迹为GPS记录的实际航迹，“＊”状轨迹为修正后的轨迹。

从图5中可以明显看出修正后的轨迹和GPS记录轨迹更为接近，说明该修正方法可以有效减小因为浮标阵元位置不准确造成的系统定位偏差。

图5 轨迹修正对比图

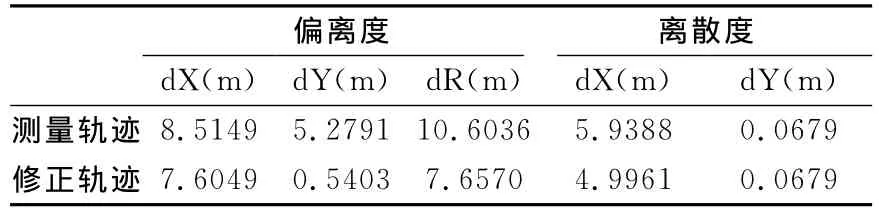
表5 测量轨迹修正精度对比

表5中的数据对比看出修正后的精度比原始测量数据有一定的提高，但只是航迹数据的位置的准确度得到了修正，经纬度的离散度基本没有变化，也就是说该修正方法对随机误差造成的影响没有修正效果。

5 结语

通过上述仿真分析验证和对实测轨迹数据进行修正对比，证明本文提出的通过流速和流向来修正阵元位置参数的方法可以对浮标式测量系统的定位准确性起到有效的提升作用。当然，这种方法只适用于对水下接收单元为软连接的电缆水听器的浮标，对于硬连接的水下接收单元，就只能对浮标安装姿态测量传感器来准确修正浮标及接收单元的实时位置数据。

[1]封金鑫，丁士圻，等.水下运动目标长基阵定位解算研究[J].声学学报，1996，18（5）：22－23.

[2]于平.两种水声导航定位算法的应用与分析[J].靶场试验与测量，2004，1（1）：12－16.

[3]吴永亭，周兴华，杨龙.水下声学定位系统及其应用[J].海洋测绘，2003，23（4）：18－21.

[4]刘林泉.水声精确跟踪导航与声通信关键技术研究[D].哈尔滨：哈尔滨工程大学博士学位论文，2007：78－86.

[5]王先华.长基线水下导航定位系统测阵及系统集成[D].哈尔滨：哈尔滨工程大学硕士学位论文，2004：35－38.

[6]付进，李利，梁国龙，等.对抗条件下的浮标基水声定位技术研究[J].兵工学报，2012，12：23－27.

[7]张红梅，赵建虎，等.水下导航定位技术[M].武汉：武汉大学出版社，2010：52－57.

[8]王逸林.水下目标跟踪系统声学信号处理[D].哈尔滨：哈尔滨工程大学，2002：13－30.

[9]耿培涛.水下高速目标轨迹测量系统信号处理软件设计[D].哈尔滨：哈尔滨工程大学，2008：17－28.

[10]付进.长基线定位信号处理若干关键技术研究[D].哈尔滨：哈尔滨工程大学，2007：30－109.