用于认知雷达的目标跟踪滤波算法研究
2013-08-10俞道滨吴彦鸿
俞道滨,吴彦鸿,赵 彬
(1.装备学院,北京101416;2.解放军63892部队,洛阳471003)
1 认知雷达及跟踪滤波算法概述

图1 认知雷达的整体结构图
2006年,国际著名信号处理专家Simon Haykin首次提出了认知雷达的概念[1],并随后发表多篇文章[2-5]对认知雷达系统各部分的实现进行了说明。认知雷达将跟踪系统、波形发射系统以及目标场景视为一个闭环的整体,通过对波形的实时调节实现对目标的有效跟踪,提高了雷达的跟踪性能。认知雷达的整体结构如图1所示。
在认知雷达的概念提出以后,许多研究者应用 该思想提出了多种具体实现的方法,对认知雷达的波形设计、检测与跟踪算法、先验知识的应用、场景分析等各方面进行了深入的研究[6-7]。
对于认知雷达的目标跟踪算法,应用Simon-Haykin在文献[4]中提到的算法,他的学生Xue Yanbo在有关认知雷达的第1篇博士论文[8]——认知雷达理论与仿真中,在接收端利用求容积卡尔曼滤波器近似最优贝叶斯滤波器,针对直线运动、垂直降落和高维空间运动3种模型的目标跟踪进行了仿真,表明引入认知能力可以提高雷达的性能。对于跟踪机动目标的应用,文献[9]应用交互多模型建立运动模型,跟踪滤波也是采用容积卡尔曼的方法。文献[10]仅就目标跟踪算法仿真对比了3种非线性卡尔曼滤波方法,指出在实际应用中平方根容积卡尔曼滤波的优点。文献[11]在实际应用中无杂波和有杂波2种环境下对自适应目标跟踪算法进行了讨论。
由于认知雷达的发展仍处于起步阶段,当前大部分的研究仍是针对理想的条件。假设在目标线性运动、环境为高斯噪声情况下,此时卡尔曼滤波就是最优的贝叶斯滤波器,可以通过目前较为成熟的卡尔曼滤波来解决目标跟踪的问题。然而在大部分情况下会遇到的是离散时间非线性滤波的情况,此时卡尔曼滤波将不再适用,需要针对不同的情况,采用拓展卡尔曼滤波、无迹卡尔曼滤波、求积卡尔曼滤波等。考虑到认知雷达变波形的实时性要求,要求算法在保证精度的同时,尽可能缩短处理时间,因而在本文中讨论几种免微分运算的状态估计方法,利用加权统计线性回归技术,通过采样点捕获系统的相关统计参数。无迹卡尔曼滤波方法(UKF)通过无迹变换确定1组加权采样点逼近随机变量的分布函数,捕获随机变量经非线性转换后的统计特性。容积卡尔曼滤波(CKF)使用基于容积原则的数值积分方法,计算非线性变换的随机变量的均值和协方差,实现简单且滤波精度较高。平方根容积卡尔曼滤波(SRCKF)是在容积卡尔曼的基础上发展而来的,起初是为了减轻跟踪滤波过程中的发散与不稳定,其算法直接通过后验误差协方差和预测误差协方差的传递而免去了对矩阵分解的操作。
2 跟踪滤波算法对比
由贝叶斯估计原理可知,基于高斯假设的贝叶斯滤波估计算法的核心在于求解具有“非线性函数高斯密度”形式被积函数的加权积分,这是高斯域贝叶斯估计算法所具备的基本特性。考虑一多维加权积分,其基本形式如下:

式中:D为积分区域,并且对于任意x∈D的权重函数w(x)已知。
假定w(x)具有高斯特性,则上式所示即为一高斯权积分问题。对于上式积分问题通常采用数值积分的计算方法。该方法的基本问题是确定一组点集及其相应的权值以用于近似求解,即:

基于上述基本问题,采用一种基于求积原理的方法解决非线性滤波的基本问题。UKF和CKF的主要区别在于权重函数w(x)的选取不同,其选择特点如图2、图3所示。

图2 UKF的sigma点分布图

图3 CKF的sigma点分布图
由图2、图3可知,CKF去掉了中心采样点,采用四周对称的方式选取采样点。在实际工程应用中,需要克服舍入误差引起的滤波发散,由于CKF的采样点个数为偶数个,可对中间数据进行取平方根操作,得到了平方根容积卡尔曼滤波的方法。其与CKF相比,该算法降低了计算的复杂度,获得了更高的效率,同时保证了协方差矩阵的非负定性,有效避免了滤波器的发散,提高了滤波的收敛速度和数值稳定性。
3 容积与平方根容积卡尔曼滤波
3.1 求容积规则
考虑下边的求积分问题:

为了计算上述积分问题,首先要将其变换至一个更为通用的球面径向积分形式,需要将x分解为一个与半径r和方向向量y相关的过程。
假设x=ry,yTy=1,则上式积分可写为:

式中:Un为半径是1的球表面;σ(·)为属于积分域Un的元素。
则:

针对以上两式,分别采用mr点Gauss-Hermite求积分规则和ms点Spherical规则,可得到mr×ms点的Spherical-Radial求容积规则为:

取mr=1,ms=3,可得到3自由度的Spherical-Radial求容积规则。
根据上述求容积规则,n维标准状态分布与非线性函数乘积的积分可近似为:

当随机变量x服从N(x;μ,Σ)的分布时,可得:
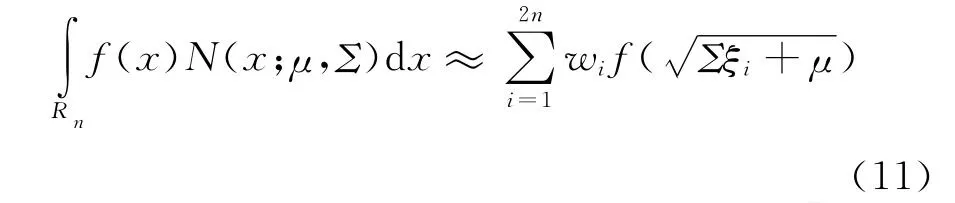

3.2 容积卡尔曼滤波
考虑如下的非线性离散状态空间模型:

式中:f(xk)和h(xk)为已知函数;wk和vk为相互独立的零均值高斯白噪声序列,其协方差矩阵分别为Qk和Rk。
将求容积计算积分的思想应用于高斯贝叶斯估计,即可得到如下标准CKF算法:
(1)时间更新
预测状态向量和预测误差协方差为:

(2)量测更新
由以下公式得到预测量测协方差矩阵和互协方差矩阵:
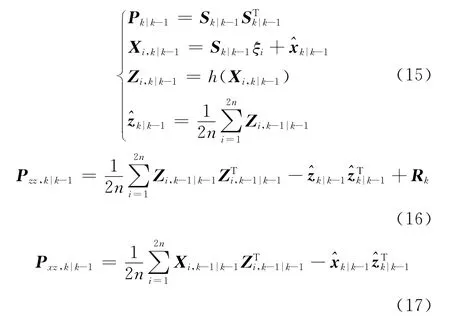
(3)计算卡尔曼滤波增益、状态估计值、状态估计误差协方差

3.3 平方根容积卡尔曼滤波
(1)时间更新
公式(13)运算不变,直接运算得到估计预测误差协方差矩阵的平方根,公式如下:

式中:QR(·)为进行正交三角(QR)分解的运算。
(2)量测更新
通过均方根直接预测量测协方差矩阵和互协方差矩阵:


(3)计算卡尔曼滤波增益、状态估计值、状态估计误差协方差

4 仿真验证
假定一匀速直线运动的目标,由单个观测站对其运动的距离和速度进行观测,运动模型写成如下形式:

仿真中,运动目标及雷达的相关参数设置如下:雷达扫描周期为1s,进行60次扫描,目标的初始状态矩阵为[-100,2,200,10],雷达观测站坐标为(200,300)。
从模型上看,状态方程是线性的,而观测方程是非线性的,点目标与雷达的距离较近,运动速度也较低,因而在跟踪时产生的误差相对较小。此处分别应用UKF、CKF、SCKF 3种滤波算法对目标进行跟踪,通过sigma点的选择逼近观测。在进行100次蒙特卡罗仿真试验后,得到3种算法下所用时间及跟踪误差的对比结果。

表1 3种滤波算法100次运算所用时间对比
综合以上图表,分析可知各种算法的估计精度及计算复杂度。就CKF与UKF相比,CKF运算的时间略长,就单次运算而言,二者的时间差距可以忽略不计,但是CKF的滤波精度较高,在近距离的情况下误差较小,比UKF的性能更好一些。随着跟踪时间的增加,CKF与UKF的性能趋于一致,误差近似相等。而SCKF与CKF和UKF相比,SCKF直接运算得到估计协方差的平方根,运算所需的步骤较少,因而所花的时间较短,但是就跟踪精度而言,仅就协方差的估计精度上,SCKF算法在跟踪的初始阶段精度最高,比CKF和UKF相比精度提高了一倍多,得到了很好的跟踪效果。随着目标远离观测点,SCKF的跟踪精度急剧变差,甚至在跟踪的末端误差达到了CKF和UKF的2倍多,相应得到的滤波轨迹也相差甚远。

图4 UKF、CKF和SCKF跟踪滤波误差对比图
由以上讨论可知,在认知雷达的应用中,一方面,由于其根据先验知识及环境信息不断变换发射波形,发射机需要在短时间内作出相应的改变,这就需要减少跟踪处理的时间;另一方面,在较短的时间内,需要较高的跟踪精度以更好地模拟目标的运动轨迹,从而为下一步的波形变化提供有力的支撑。在高斯噪声、线性运动目标的条件下,通过平方根容积卡尔曼滤波算法得到的跟踪效果与认知雷达的实际要求较为吻合,适用于波形变化条件下对目标的短时跟踪,并能获得更加准确的运动轨迹,跟踪精度较高。
5 结束语
本文首先对当前认知雷达的研究现状进行了简介,对其跟踪滤波部分应用的算法进行了详细的讨论,在认知雷达对跟踪滤波苛刻要求的基础上,详细比较了免微分运算的无迹卡尔曼、容积卡尔曼、平方根容积卡尔曼3种滤波算法,结果表明,对高斯噪声环境中的线性运动目标进行跟踪滤波较为适合的算法是平方根容积卡尔曼,其在跟踪精度和实时性要求两方面均满足要求。本文仅在理想条件下进行了相关讨论,对于在复杂运动和引入杂波后的算法选择,需要进行进一步的研究,以满足在认知背景下雷达跟踪性能的整体提升。
[1]Haykin S.Cognitive radar:a way of the future [J].IEEE Signal Processing Magazine,2006,23(1):30-40.
[2]Haykin S.Cognitive dynamic systems[A].IEEE International Conference on Acousticcs speech and Signal Processing[C].Hawaii,2007:1369-1372.
[3]Haykin S,Yanbo Xue,Timothy N.Davidson optimal waveform design for cognitive radar[A].IEEE Conference on Signals,Systems and Computers[C].Califonia,2008:3-7.
[4]Arasaratnam I,Haykin S.Cubature kalman filters[J].IEEE Transaction on Automatic Control,2009,54(6):1254-1269.
[5]Haykin S,Amin Zia,Arasaratnam I,et al.Cognitive tracking radar[A].IEEE Radar Conference[C].Virginia,2010:1467-1470
[6]Ric A Romero.Matched waveform design and aadaptive beamsteering in cognitive radar applications[D].Arizona:The university of Arizona,2010.
[7]Guerci J R,Baranoski E J.Knowledge-aided adaptive radar at DARPA:an overview [J].IEEE Signal Process,2006,23(1):41-50.
[8]Xue Yanbo.Cognitive Radar:Theory and Simulations[D].Canada Hamilton:McMaster University,2010.
[9]Mingjie Wan,Pengfei Li,Tao Li.Tracking maneuvering target with angle-only measurements using IMM al-gorithm based on CKF[A].2010International Conference on Communications and Mobile Computing[C],Shenzhen,2010:92-96.
[10]郝燕玲,杨峻巍,陈亮,等.平方根容积卡尔曼滤波器[J].弹舰与制导学报,2012,32(2):169-172.
[11]夏洪恩.基于目标跟踪的波形自适应选择技术[D].长沙:国防科技大学,2010.
