一种Godunov算法及其在非平底流污染物传输中的应用
2013-08-09杨金波段文刚黄国兵李订芳
杨金波,段文刚,黄国兵,李订芳
(1.长江科学院水力学研究所,武汉430010;2.武汉大学数学与统计学院,武汉430072)
一种Godunov算法及其在非平底流污染物传输中的应用
杨金波1,段文刚1,黄国兵1,李订芳2
(1.长江科学院水力学研究所,武汉430010;2.武汉大学数学与统计学院,武汉430072)
采用和谐的加权平均通量(Weighted Average Flux,简称WAF)算法,研究了浅水波方程的间断解及污染物传输问题。该算法采用WAF格式和HLLC Riemann求解器近似单元边界数值通量,中心差分格式离散地形源项,然后理论上证明了该算法是和谐的。最后利用WAF算法对非平底地形上浅水波间断解及污染物传输问题进行数值计算,精确地捕捉到了间断解和污染物运动过程,结果表明该算法满足守恒性,具有高分辨率、无振荡及捕捉污染物运动边界的能力。
浅水波方程;WAF格式;溃坝;污染物传输
1 研究背景
河流、湖泊和近海岸的污染问题越来越严重,一方面破坏了生态环境;另一方面对人类生命安全和经济发展带来致命性的危害,因此有必要研究污染物传输方式的数学模型。
污染物传输的数值算法包括浅水波和污染物传输扩散的计算。在浅水波方程计算方面,近年来空气动力学中的Godunov[1]型有限体积算法越来越普遍地应用到浅水波方程中,WAF方法[2]是Toro基于Godunov思想提出的显示、二次精度的守恒有限体积格式。非平底河床是浅水方程计算的一个关键问题,为了构造和谐的数值格式,Roe[3]提出迎风离散双曲型方程中源项的思想;Bermudez和Vazquez Cendon[4]用迎风离散源项的方法计算了浅水波方程;Hubbard和Garcia Navarro[5]用迎风离散源项的方法构造了平衡源项和通量梯度的二阶格式;Zhou[6]等人对二维浅水波方程提出了水位梯度法。对于污染物传输部分,考虑对流占优的问题,文章采用垂直方向平均的传输方程,忽略了扩散项。数值求解时,污染物传输方程作为整个系统的一个波系,同浅水方程耦合求解。
本文首先构造了浅水波方程和污染物扩散方程的二阶精度和谐WAF格式,然后用该算法研究了非平底河床上浅水流的间断解及污染物传输问题,将计算结果同精确解或其他文献比对,证明该方法的计算结果精度高、分辨率高,能计算真实的溃坝和污染物传输问题。
2 数值格式
2.1 浅水波及污染物传输方程
控制方程由浅水波方程和污染物运输方程组成,其中,污染物部分主要研究污染物传输过程,忽略污染物扩散项,如

式中:H=h+b(x)为水位高程;h为水深,b(x)为河床高程;q=hu为单宽流量;u为流速,传输标量r=hc;c为污染物浓度;g为重力加速度。
2.2 WAF有限体积格式
对式(1)关于区间[xi-1/2,xi+1/2]×[tn,tn+1]积分,并应用格林(Green)公式,则得有限体

项,这里采用TVD WAF格式给出数值通量,中心差分格式离散源项。如图1所示,假设局部Riemann问题自相似解仅有激波结构,TVD WAF格式[7]的数值通量为


图1 局部Riemann问题自相似解的波结构Fig.1 W ave structure of self sim ilar solution for local Riemann problem

其中:

式(4)中变量p可以为任意一个在波k处变化的物理量,这里取p(k)=H,k=1,3…;p(2)=r,k=2。
为了计算FWAFi+1/2,采用HLLC解法器[6]来近似Riemann问题自相似解的中间状态,
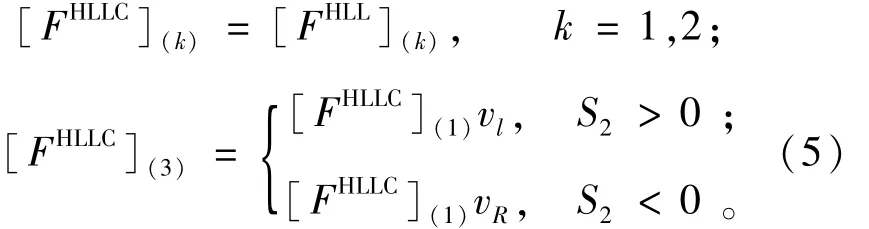
下标(k)表示通量向量的第k项,其中HLL求解器定义为
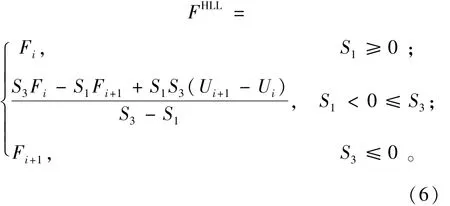
左右波速度S1和S3通过文献[7]给出,即

式中


当出现干湿边界时S1,S3分别调整:
左干河床
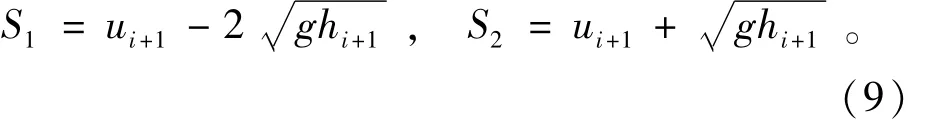
右干河床

此时,式(8)中的S3会自动和估计的干河床式(9)或式(10)重合。
为保证数值格式的稳定性,时间步长
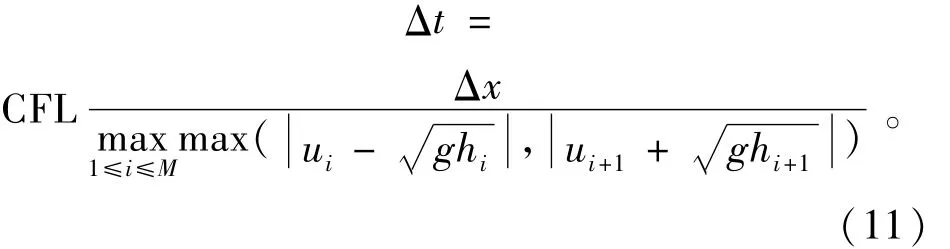
其中CFL(0<CFL≤1)是Courant数。
地形源项采用中心差分格式进行离散

2.3 和谐性质证明
为了证明WAF格式的和谐性,只需证明静态条件q=0 m,H=常数及r=常数时,下式成立

由TVD WAF格式的数值通量定义式(3)和静水条件,单元Ii右边界xi+1/2处的数值通量为
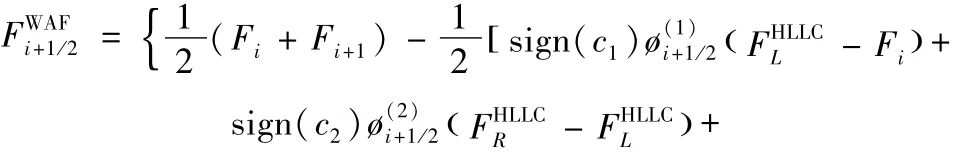

将式(14),式(15)和式(16)分别代入式(13)很清楚地证明格式满足和谐性。
3 算 例
这里利用WAF格式对非平底间断浅水波方程中污染物传输问题进行了数值计算,研究了溃坝波传播过程中污染物的传输过程和机理,试验结果表明该算法可以精确地捕捉激波和污染物传输边界,无振荡。
3.1 梯形河床上的污染物传输问题
本算例[8]梯形河床定义为

计算步长Δx=0.08 m,CFL=0.9。T=1 s时计算结果如图2所示。WAF算法计算的水位和HLLC格式计算的水位吻合较好,同时由图3可知,WAF格式对污染物运动的计算比一阶精度的HLLC格式分辨率要高,WAF算法的计算数值耗散低。

图2 水面线Fig.2 W ater surface profile
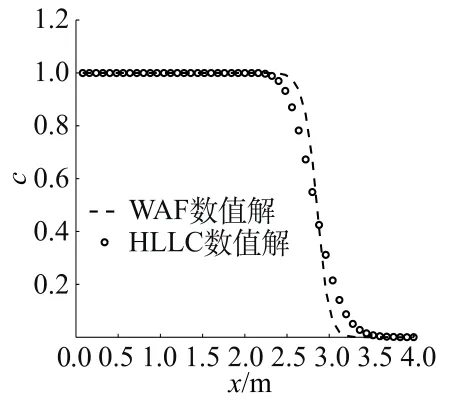
图3 污染物分布Fig.3 Pollutant distribution
3.2 溃坝波中的污染物传输问题
本算例研究了溃坝过程中污染物传输规律,计算区域为2 000 m长的平底无摩擦河道,溃坝初始条件如下:
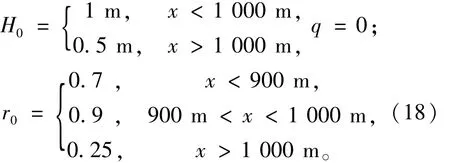
采用100个计算单元,CFL=0.9。T=250 s时计算水位和单宽流量如图4所示,可以看出WAF格式比HLLC格式计算的更逼近解析解。在污染物计算方面,如图5,WAF计算的污染物区域比HLLC格式窄,浓度更高,说明WAF比HLLC在数值计算方面的耗散低,精度高。

图4 水位和单宽流量Fig.4 W ater level and discharge per unit w idth

图5 污染物中心分布Fig.5 Distribution of pollutant center
3.3 带干湿河床的污染物传输问题
该算例利用WAF算法研究干湿河床上的污染物传输问题[9],初始条件为:

其中地形定义为

空间步长Δx=0.1 m,CFL=0.8。t=0.25 s时,计算结果如图6所示。WAF格式计算的水位能很好的和参考值吻合(该算例没有解析解,可采用HLLC格式在2 000个网格下的计算结果作为参考值)。并且精确地捕捉到阻碍物左边x=25/3 m处的激波和x=6.5 m处的水面涌起。同时,分析t=0.18 s时污染物运动状态,如图7。可以看出WAF比HLLC格式精度高。进一步,由初始条件产生的向左和向右运动的2个稀疏波中间形成干河床,改进后的WAF算法可以很好处理干湿边界问题。该算例说明WAF算法具有高精度、高分辨率,及能处理复杂干河床问题,具有真实问题的处理能力。

图6 T=0.25 s时刻水面线Fig.6 W ater surface profile at T=0.25 s

图7 T=0.18 s时污染物分布Fig.7 Pollutant distribution at T=0.18 s
4 结 语
本文利用二阶精度和谐WAF格式研究了浅水波方程和污染物扩散问题,研究了污染物在溃坝、非平底河床情况下的传播机理计算结果同精确解或其他文献比对,证明该方法是高精度、高分辨率,能计算真实的溃坝和污染物传输问题。
[1] GODUNOV SK.Finite Difference Methods for the Com putation of Discontinuous Solutions of the Equations of Fluid Dynamics[J].MatematicheskiǐSbornik,1959,47:271-306.
[2] TORO E F.AWeighted Average Flux Method for Hyper bolic Conservation Laws[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sci ences,1989,423(1865):401-418.
[3] ROE L P.Upwind Differencing Schemes for Hyperbolic Conservation Laws with Source Terms[C]∥Springer Verlag.Proceedings of an Advanced Research Workshop:Nonlinear Hyperbolic Problems:Lecture Notes in Mathe matics,Volume 1270.St.Etienne,France January 13-17,1986:41-51.
[4]BERMUDEZA,VAZQUEZ CENDON EM.Upwind Meth ods for Hyperbolic Conservation Laws with Source Terms[J].Computers and Fluids,1994,23(8):1049-1071.
[5] HUBBARD E M,GARCIA NAVARRO P.Flux Differ ence Splitting and the Balancing of Source Terms and Flux Gradients[J].Journal of Computational Physics,2001,165(1):89-125.
[6] ZHOU G J,CAUSON M D,MINGHAN G C,et al.The Surface Gradient Method for the Treatment of Source Terms in the Shallow Water Equations[J].Journal of Computational Physics,2001,168(1):1-25.
[7] GALLOU?T T,H?RARD JM,SEGUIN N.Some Ap proximate Godunov Schemes to Compute Shallow Water Equations with Topography[J].Computers and Fluids,2003,32(4):479-513.
[8]TORO E F.Shock Capturing Methods for Free Surface Shallow Flows[M].Chichester:Wiley,2001.
[9]FERNANDEZ NIETO E D,NARBONA REINA G.Exten sion of WAF Type Methods to Non homogeneous Shallow Water Equations with Pollutant[J].Journal of Scientific Computing,2008,36(2):193-217.
(编辑:王 慰)
Application of a Godunov Type A lgorithm to the Pollutant Transport w ith Irregular Bedslope
YANG Jin bo1,DUANWen gang1,HUANG Guo bing1,LIDing fang2
(1.Hydraulics Department,Yangtze River Scientific Research Institute,Wuhan 430010,China;2.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
A well balanced weighted average flux(WAF)scheme is proposed for the nonhomogeneous shallow water equations with pollutant transport.Thewater surface elevation and water discharge are used as the conserved varia bles in the shallow water equations,while the conserved variables and the bed elevation are set on the staggered mesh.Here,theWAF scheme combined with the HLLC Riemann solver is directly performed for the nonhomoge neous shallow water equationswith pollutant transport,and the spatial second order central difference approximation is applied to source terms.Then,it’s proved that the extended WAF scheme is harmonious in theory.Finally,several numerical tests about the steady and nonsteady flows over the irregular bottom or with the wet/dry front are simulated.The results obviously suggest that the WAF scheme is a well balanced,robust,efficient,and practical scheme with high resolution.
shallow water equations;WAF scheme;dam break;pollutant transport
X52
A
1001-5485(2013)08-0097-05
10.3969/j.issn.1001-5485.2013.08.021
2013,30(08):97-101
2013-04-16;
2013-06-19
国家自然科学基金资助项目(11102027);中央级基本科研业务费项目(CKSF2011014/SL,CKSF2013025/SL,CKSF2012010/SL)
杨金波(1982-),男,山东德州人,工程师,博士,主要从事计算流体力学,(电话)027-82823698(电子信箱)yangjb1225@163.com。
