中空内外钢管混凝土风电塔架柱有限元分析

屈成忠，王祺，熊向芝

(东北电力大学建筑工程学院，吉林市 132012)

0 引言

随着能源危机和环境污染问题的日益突显，越来越多的人开始关注风能［1］。当应用于风力发电的风机运行时，塔架柱受力状态复杂，包括风机自重和叶片旋转时对塔架柱施加的载荷等。塔架柱作为风力发电机组的重要支撑结构，高度都在几十m以上，其质量占风机总质量的一半左右，成本占总制造成本的18%左右，保证塔架柱的设计质量才能保证风力发电机安全运行［2］。因此设计塔架柱时，不仅要使其满足工程要求，还要考虑经济性。

20世纪90年代，世界各国学者对中空内外钢管混凝土柱力学性能的研究取得了很好的成绩［3-5］，日本首先将其应用于高架桥的桥墩并取得了良好的效果。近年来，钢混组合结构越来越被广泛应用在实际生活中，但将中空内外钢管混凝土应用到风力发电机组塔架柱的还很少见到。

中空内外钢管混凝土柱是在2个同心放置的钢管之间灌注混凝土而制成的构件，这种构件既保持了钢管混凝土的基本优点，而且与实心钢管混凝土相比，又具有自重轻、截面开展、抗弯刚度大和防火性好的特点［6］，其承载力以及经济性都优于钢混结构，因此具有更广阔的应用前景。基于以上优点，本文将其应用于1.5 MW风力发电机组塔筒中，对中空内外钢管混凝土风力发电机组塔架柱的设计方法和力学特性进行研究。

1 中空内外钢管混凝土塔架柱设计

本文设计原型是1.5 MW三桨叶风力发电高塔系统。利用应力等效原则和刚度等效原则，对中空内外钢管混凝土风力发电机组塔架柱进行设计。塔架柱设计高度为65 m，其圆截面形式如图1所示。图中:Do为外钢管外直径;Di为内钢管外直径;to为外钢管厚;ti为内钢管厚［7］。

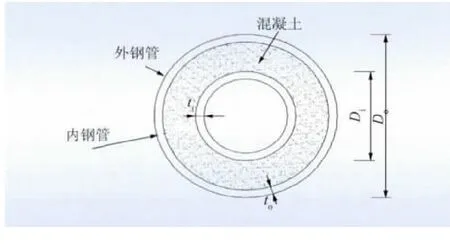
图1 中空内外钢管混凝土截面图Fig.1 Sectional view of concrete filled double skin steel tubes

GB 50017—2003《钢结构设计规范》给出:不出现圆钢管轴压局部屈曲时的临界径厚比限制为100。美国的ANSI/AISC设计规范中给出圆钢管受弯时的承载力计算方法，根据截面径厚比不同分为弹性抗弯承载力、塑形抗弯承载力、弹塑性抗弯承载力;对于受弯构件给定屈服强度为345 MPa时圆钢管的最大径厚比限值为253。

考虑到内外钢管之间填充了混凝土，外钢管径厚比的限值取钢管局部稳定限值的1.5倍;内钢管径厚比的限值可按钢管的有关规定取值［7］。

2 塔架柱有限元建模

2.1 塔架柱模型

风力发电机组主要包括叶片和塔架柱2个弹性体，其中塔架柱是主要承重结构，支撑着机舱、轮毂、叶片及其他附属构件，因此，塔架柱的振动应该是耦合振动［8］。考虑到结构的动态特性，固有频率的大小与结构的质量和刚度相关，而结构阻尼对自振频率影响甚小［9］。为简化计算，忽略阻尼的影响，在塔架柱顶端创建1个mass21质量单元节点来模拟机舱、轮毂和叶片的影响。质量点的位置是三者的重心位置，距塔顶的高度为1.46 m，距塔架柱中轴线的距离为1.2 m。其质量为三者之和，总体转动惯量为三者各自在合重心位置的转动惯量之和。

由于SHELL181单元可用来模拟由多层复合材料所组成的结构，并且壳单元能很好地模拟弯曲以及中面内力，所以中空内外钢管混凝土塔架柱采用壳单元SHELL181最为合理。在应用该单元之前，需给出不同材料的属性和厚度［10］。首先应将塔体沿壁厚方向分为3层，即内钢管、外钢管和混凝土层;塔高65 m，塔底直径4 m，塔顶直径2.5 m，其中塔底外钢管壁厚16 mm，混凝土壁厚125 mm，内钢管壁厚9 mm。忽略法兰连接，可认为塔筒是连续的变截面锥形筒体结构，塔身高度范围内的壁厚和直径按照线性变化;塔架柱筒壁的材料为Q345钢，弹性模量为2.1×1011N/m2，密度为7850 kg/m3，泊松比0.3;混凝土标号C75，泊松比0.2，弹 性 模 量 为 3.7 × 1010N/m2，密 度 为2400 kg/m3。爬梯、平台及其他附属结构，由于质量较轻，因此不考虑其结构，只把其质量加到塔架柱上。

2.2 边界条件和计算荷载

因为风力发电机塔筒的底端固定在地基上，可近似认为塔架柱与地基是刚性连接，不考虑土体对结构的影响［11］;钢管和混凝土之间无滑移，两者之间的变形协调;为了避免构件之间出现滑移，采用多点约束单元(MPC184)来实现质量点和塔架柱的连接。图2为风力发电机塔架柱有限元模型;塔顶坐标系见图3。

图2 塔架柱有限元模型Fig.2 Finite element model of tower

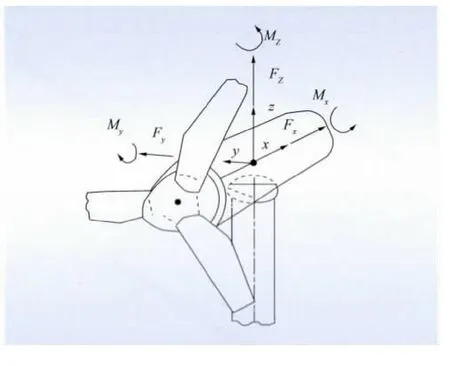
图3 塔架柱坐标系Fig.3 Coordinate system of tower

3 塔筒静强度分析

3.1 工况设定

本文主要研究风力机在不同工况下，结构的静力选型问题，故将复杂的工况制定过程简化为:

3.2 塔架柱顶部中心荷载

计算分析3种工况下的静力荷载，通过塔顶坐标系将其施加到塔架柱上，计算得到的荷载值见表1。表中:Mx、My、Mz分别为绕 x、y、z轴的弯矩;Fx、Fy、Fz分别为沿 x、y、z轴的力。

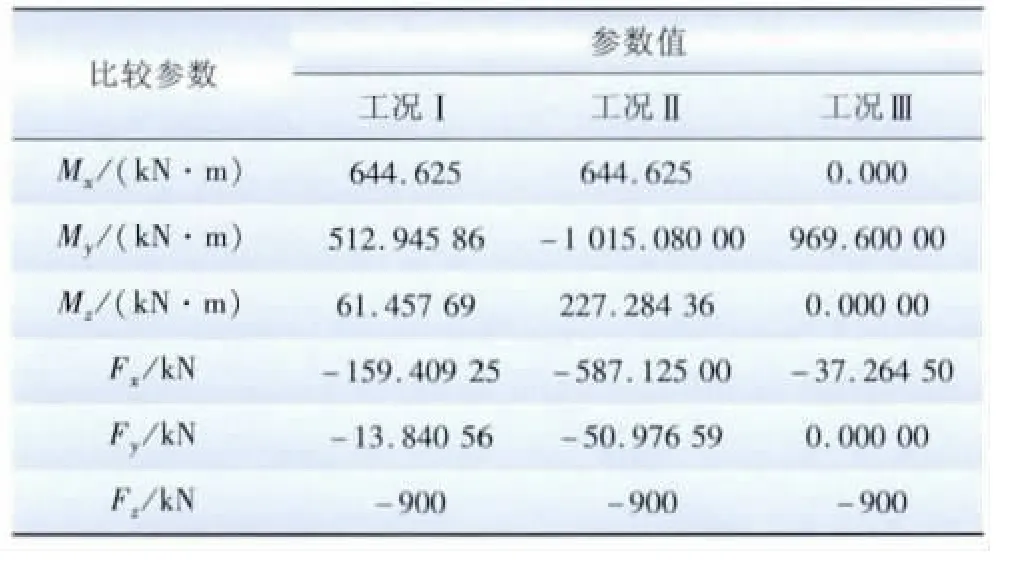
表1 塔架柱顶部荷载Tab.1 Top load of tower

由表1可知:在3种工况下，塔架柱底部的等效应力最大，顶部的位移最大;应力值随塔架柱高度的增加而减小，其中塔底最大应力分别为17.6、52、7.08 MPa。塔架柱等效应力云图见图4。位移大小随塔架柱高度的增加而增大，最大位移分别为59.078、231.205、4.649 mm，3 种工况下的最大应力和最大位移如表2所示。

图4 塔架柱在各种工况下的应力分布Fig.4 Stress distribution of tower under different conditions

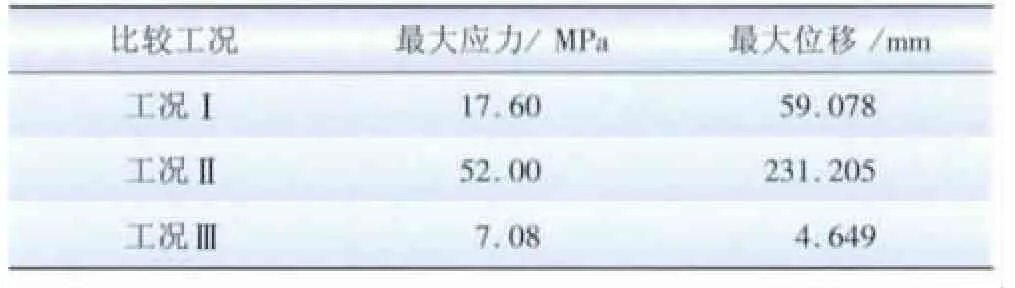
表2 中空内外钢管混凝土塔架柱分析结果Tab.2 Analysis results of concrete filled double skin steel tube tower

塔架柱允许的最大变形为塔高的0.5%～0.8%［2］，Q345 钢的允许拉压应力为 345 MPa，考虑安全系数1.5，取极限值为230 MPa。因此，由上述结果可知，在工况II下，塔架柱应力和位移均最大，分别为允许限值的20.4%、0.3%，均在安全范围内。

4 塔架柱的模态分析

4.1 模态分析的理论基础

固有频率和振型是结构的动力特性，由于阻尼对结构的固有频率影响非常小，故可以忽略阻尼的影响，其振动方程为

假设结构的自由振动是简谐运动，即 q=Φ×sin( ωt+θ)，代入式(1)得结构的广义特征值方程为

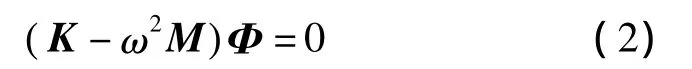
式中:ω为结构的自振频率;Φ为振型向量。

4.2 风力发电塔系统的模态分析

模态分析时，对塔架柱底部的位移进行约束，各个自由度均设为0。采用 Block Lanzos模态提取法［13］，由于进行模态分析时主要考虑的是塔筒低阶模态，故只提取5阶模态，如表3所示。

表3 塔架柱的前5阶模态Tab.3 Top 5 order modal of tower

根据相关规定，设计塔架柱时，应避免其固有频率与叶片旋转频率发生共振，这就要求塔架柱固有频率应在风轮旋转的1倍和3倍频率的±10%范围之外［2］。本文设计的风力机含3片桨叶，风轮转速为19 r/min，风轮旋转频率为0.32 Hz，过桨频率为0.96 Hz。由表3可以看出塔筒的1阶固有频率避开了风轮旋转频率和过桨频率的10%以上，满足工程要求。因此，风机正常工作时塔架柱不会与叶片发生共振。

5 结论

(1)塔架柱在额定风速和切出风速下正常运行以及极端风况下停机这3种工况下的最大应力处均为塔筒底部，随着高度增加，应力逐渐减小，因此塔架柱按变截面来设计是合理的。

(2)由静力分析得出，额定风速下正常运行和极端风况下停机时塔架柱的最大应力和位移较小，而切出风速下正常运行使塔架柱出现最大应力与位移，在设计中应着重考虑此工况。

(3)由模态分析可以看出，塔架柱的低阶频率在安全范围之内，高阶频率远离共振区域，所以塔架柱不会发生共振。

［1］Bose B K.Energy environment and advances in power electronics［J］.IEEE Transaction on Power Electronics，2000，15(4):688-701.

［2］白海燕，高俊云，杨兆建.兆瓦级风力发电机组塔架的静强度及模态分析［J］.机械工程与自动化，2010(6):34-36.

［3］Schneider S P.Axially loaded concrete-filled steel tubes［J］.Journal of Structural，ASCE，1998，124(10):1125-1138.

［4］Zhao X L，Grzebieta R，Elchalakani M.Tests of concrete-filled double skin circularhollow sections［C］//Proceedings ofthe First International Conference on steel ＆ Composite Structures，Pusan，Korea:Techno-Press，2001:283-290.

［5］Mark A B.Design strength of slender concrete-filled rectangular steel tubes［J］.ACI Structural Journal，1996，93(2):229-235.

［6］Yagishita H，Kitoh M，Sugimoto T，et al.Double skin composite tubular columns subjected to cyclic horizontal force and constant axial force［C］//Proceedings of 6th International Conference on Steel and Concrete Composite Structures，USA:ASCCS －6 Secretariat，Dept.of Civil Engineering，University of Southern California，2000:497-503.

［7］宋博.钢－混凝土风力发电机组塔架设计及振动特性［J］.山西建筑，2009，35(8):80-81.

［8］李声艳，徐玉秀，周晓梅.风力发电机组风轮的动态特性分析［J］.天津工业大学学报，2006，25(6):65-37.

［9］单光坤，姚兴佳.兆瓦级风力发电机组的模态分析［J］.沈阳工业大学学报，2008，30(3):276-279.

［10］贺广陵，李杰.风力发电高塔系统风致动力响应分析［J］.电力建设，2011，32(10):1-9.

［11］Lavassas I，NikolaidisG，Zervas P，et al.Analysis and design of the prototype of a stell1 － MW wind turbine tower［J］.Engineering Structures，2003，25(8):1097-1106.

［12］赵荣珍，吕刚.水平轴风力发电机塔筒的振动模态分析［J］.兰州理工大学学报，2009，35(2):33-35.

［13］楚晨晖，陈少林，柯世堂.风力发电机高塔系统的自振特性及参数分析［J］.电力建设，2013，34(1):16-20.