基于RBF神经网络的三基色配比研究
2013-08-08文蒸肖辉
文蒸肖辉
(同济大学电子与信息工程学院,上海 201804)
1 引言
色温 (CT,color temperature)和显色指数(CRI,color rendering index)是光源评价的重要指标,都是在三基色原理的基础上进行的计算。目前光源色温的计算已有相关研究[1]~[5],但各种算法的预测精度存在不同程度的误差,所需数据相当庞杂,计算量也很大,对于不同使用者而言,这些算法选择性较大,可操作性太随意,同样的,显色指数的计算研究也存在这方面问题[6]、[7],其所需的参照样板的数据表更是庞大。更为重要的是,色温和显色指数的计算是分开计算的,采用两套算法的,对于计算机编程或者单独计算,都是一件繁重、要求一定数学功底的任务。
因此,有人提出建立相应的数据库,体现在RGB光源方面,殷录桥等人在实验中测试得到一个不同色温配比的数据库,实际色温与理论计算相差无几,基本实现了类太阳光动态色温变化趋势[8];彭浩等人[9]依托 Matlab软件建立了显色指数的计算模型,只需输入参与合成的单色光源光谱就可以计算出合成后光源的显色指数。但是两者的研究还只是基于原有算法的计算机化的结果,因此,前期的数据输入仍然相当庞大,基于此,针对RGB-LED光源的光谱功率分布构成的特殊性,本文提供一种RBF神经网络建立三基色配比和色温、显色指数之间的网络模型,试图将两者联系起来,使得一组配比产生两个结果,同时还兼具简单的特点,通过Matlab软件仿真,验证了该网络模型精度高,具有很好的预测性能,可以用于实际需要。
2 径向基函数神经网络
径向基函数神经网络 (Radial Basis Function Neural Network,RBF)是人工神经网络的典型结构,它是一种三层前向逼近网络,即包含有一个输入层、一个隐含层和一个输出层,如图1所示 (图中的m、n和k表示相应层次的节点数目),具有结构简单、学习速度快、网络模型能够用数学式子表达等优点;而且,它是一种通用逼近器,能够以任意精度逼近待求解预测模型[10]、[11],特别适合于预测数据少的问题。
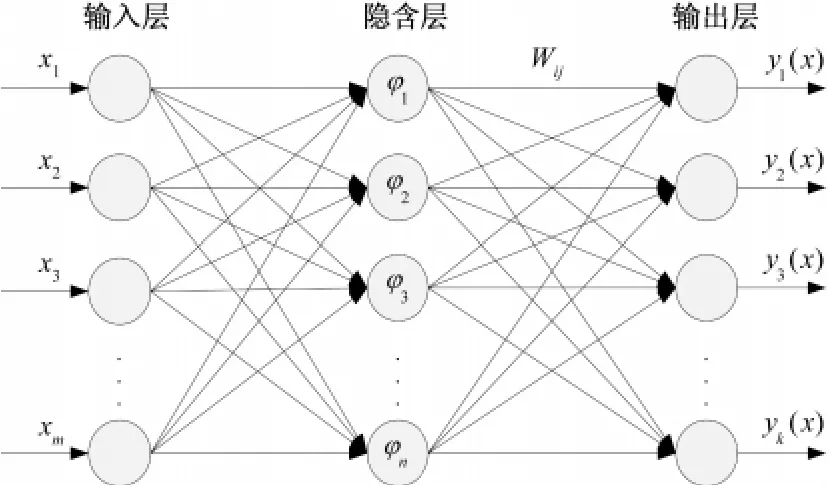
图1 RBF网络结构Fig.1 RBF neural network structure
在RBF网络中,隐含层是由一组径向基函数构成,隐含层节点通过基函数执行一种非线性变化,将输入空间映射到一个新的空间,输出层节点则在该新的空间实现线性加权组合,从而建立非线性问题的数学模型。具体结构和参量如下:假定X=(x1,x2,x3…xm)为输入向量,Y=(y1,y2,y3…yk)是输出向量,且Wij是隐含层到输出层之间的权重值,其下标表示第i个隐含层节点到第j个输出节点的连接权重;φi是关于n维空间的一个中心点具有径向对称的基函数,基函数的目的就是将低维的线性不可分的问题转化成高维空间内线性可分,以逼近任意非线性函数。
研究发现,我们采用什么样的径向基函数,对RBF神经网络函数逼近的性能几乎没有多大的影响[12],同时由于高斯函数形式简单,对于任意阶导数光滑性能优越,广泛用于各种情况下的函数逼近,即
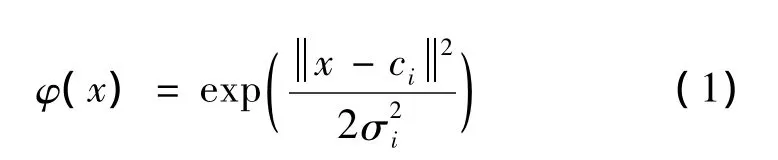
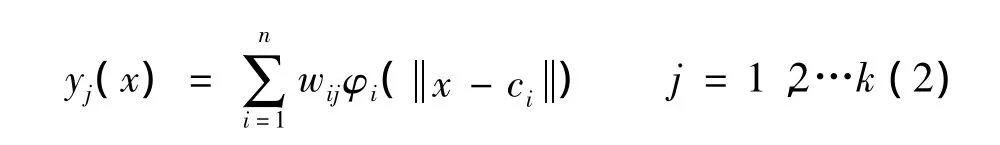
式中 k——输出节点数;
n——隐含层节点数。
在实际应用中,网络的各种参数都是通过一定的样本进行学习得出的,这样,输入和输出之间的关系就可以数学表达式表示出来。
因此,要获得理想的RBF神经网络模型,需要确定一下几个方面:
①确定样本的选择。选择实际测量的正确样本,且样本数据分布具有均衡性,这样才能正确反映所要确立模型关系的内在规律,充分照顾到各个情况下的规律性特征,从而建立具有广泛适用性的模型关系。基于神经网络算法的特点,样本的规模决定了网络训练结果的精度,而样本规模只影响训练的时间,所以样本规模只需满足实际需求即可。
②确定隐含层的结构。隐含层的节点数直接决定了RBF网络的拟合程度[12],数目过多会降低泛化能力,即用较少的样本数据进行训练,使神经网络对样本数据之外的输入也能给出合适的输出,容易产生过拟合,相反又会造成误差太大,不利于预测,所以隐含层节点数目是关键。目前还没有统一的方法来确定节点的数目,对于小规模的样本,隐含层的节点数常可以取值等于基函数中心数[13]。
③确定的函数参数有三个,分别是:RBF的中心和扩展常数以及输出神经元的权值。对于中心的选择,并没有统一的标准。一种常用的方法是根据经验选择中心,但对样本的分布均匀性要求很高,中心一旦确定,就不再发生改变,但算法无法判断样本是否选取合理;另一种就是采用聚类的方法来选择中心,有硬C均值算法、k-means算法以及最近邻聚类学习算法等。而扩展常数的大小和中心数往往成反比关系,该数值过小,就需要许多的神经元来适应,这样一来,设计的网络性能就会很不好,因此,最好的方法就是采用寻优的方式寻找合适的基函数扩展常数。而隐含层到输出层的线性关系中的权值有多种算法:梯度下降迭代法,伪逆法和最小二乘法等,但常用最小二乘法求解[14]、[15]。
3 三基色配比到色温、显色指数的RBF神经网络的模型确定
就目前的RGB-LED来说,商业应用的LED芯片或激发荧光粉后产生的蓝、黄绿和红光的峰值波长大多分别落在420~490、500~580和590~660nm区域,按照CIE显色指数计算方法,光源的显色指数与光谱功率分布密切相关,对于RGB-LED来说,单色LED的峰值波长是光谱功率分布的决定因素,不同的峰值波长的叠加会产生不同的光谱分布。一般而言,显色指数越高,光源的照明效果会越好,但由于单个LED的光谱分布与传统光源具有很大不同,因此显色指数并不能有效的反映实际照明效果,尤其是白光 LED 光源[16]、[17],而这并不是本文的重点,另外在一些特殊场合,对RGB-LED的显色指数要求并不高,比如代替汞灯使用的一些场合,因此,这里对样本输出的显色指数并不做过多要求,只要求符合样本选择的条件即可。
同时,根据三基色原理,任意色温的光源可以通过红绿蓝任意比例实现,因此可以根据不同比例的三基色LED搭配来实现不同色温和显色指数的LED光源,目前商用RGB-LED色温主要局限在2000k~6500k。
本文所使用的三基色样本选取峰值波长分别为627nm、519nm和442nm,在这个条件下,三基色的配比作为输入量,输出量为色温和显色指数。本文选用参考文献中的样本[18](见表1),其分布均匀,完全符合RBF神经网络对样本的要求。结合RBF网络性质和聚类思想,其隐含层节点数不会超过学习样本数。图2为隐含层节点个数为5时的RBF神经网络的结构。
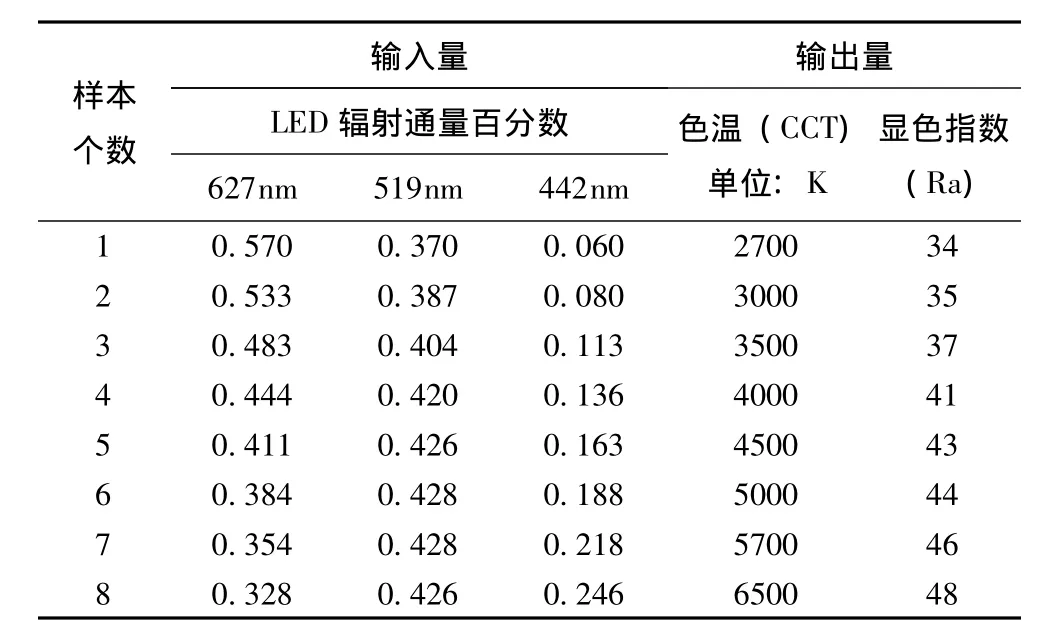
表1 RGB-LED样本Table 1 RGB-LED samples
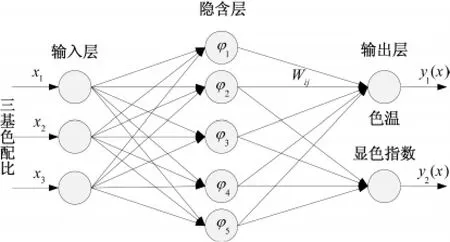
图2 三基色配比与色温、显色指数的RBF网络结构Fig.2 Three-color ratio and color temperature,color rendering index of RBF neural network structure
为了避免输入和输出数据离散程度太大,造成学习数值的溢出和出现网络预测误差大,原始数据必须进行预处理,由于输入是三基色配比数值在0到1之间,因此只需将输出数据做归一化处理。
对于输出色温来说:
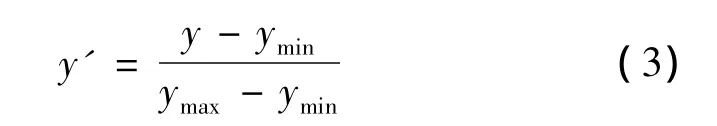
由于对于显色指数越大,效果就愈好,因此其归一化采用不同的方式:

3.1 RBF神经网络的学习和验证
本文通过样本的训练要达到目标关系的拟合,经过三个步骤:
(1)通过网络学习建立目标关系的网络模型;
(2)验证网络模型在一定误差范围下的正确性;
(3)预测在新的输入情况下,产生理想输出。
因此,本文随机将前5个样本和第8号样本选作网络的训练样本,用于网络的训练构建,剩下的样本6号作为验证样本,7号样本作为预测样本来验证网络的精度和准确性。网络的中心数和扩展常数都采用寻优的方式进行确定,而权值的确定将根据隐含层输出利用最小二乘法求解,其原理是根据式 (5)即输出层的神经元是隐含层神经元的输出加权求和,建立矩阵为确保获得最佳网络设计。在Matlab中,有专门的MSE(Mean Squared Errors,均方误差)SSE(Sum of Squares for Error,误差平方和)性能函数来判断神经网络的网络优越性。MSE数值的大小反映了数据的变化程度,其值越小,越说明该模型具有跟高的精确度用来描述数据关系,具体表达式如下:
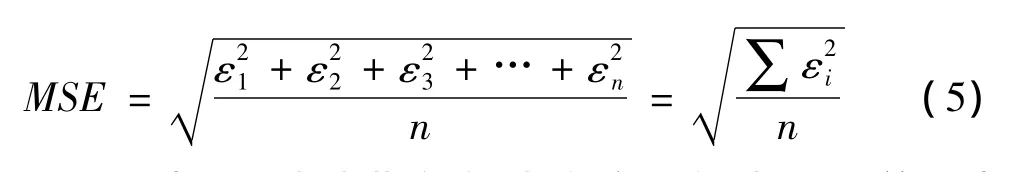
其中,εi代表期望输出和实际输出的误差。本文MSE的数值采用实际输出反归一化后的误差进行计算,因此考虑到数量级的问题,可能会呈现较大的数值。
而SSE则体现了样本实际输出值的离散状况,数值越小,越能反映网络中心具有标志性,聚类效果优异,产生的预测效果就会更好,因此该网络就具有很好的泛化能力。在神经网络学习中,此时的误差是实际输出和期望输出 (归一化后)的比较而得,考虑到精度的要求,数值上往往呈现接近于零的状态。
通过两个性能函数对不同情况下的网络模型进行判定,以寻优的方式获得理想网络模型。
3.2 输出数据要求
色温是对光源颜色的度量,人眼对颜色的可辨别颜色的容许色容差一般要求在4~5SDCM内,因此,模拟输出的色温偏差必须在一定色容差值内,否则就是无效,而国家标准GB/T24823—2009《普通照明用LED模块性能要求》其色容差仅要求小于7SCDM即可,由于不同的色温色容差要求是不同的,结合飞利浦照明公司的数据 (见表2),本文认为输出色温偏差值局限在 (-200,200)作为对结果输出有效要求。
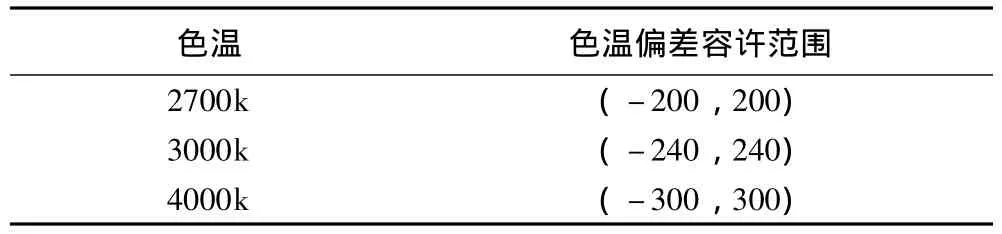
表2 一定色温允许偏差值范围Table 2 Deviation range in color temperature
对于显色指数,该数值是对光源显色性能的评价,但是,比如指数为1,具体为何种视觉感知,目前并没有对于显色指数容许范围的研究,但根据实际应用中,显色指数往往精确到整数部分,因此,本文将结合RBF网络的性能函数进行判定,使得显色指数的输出与实际值相差不超过1。
3.3 仿真结果分析
在Matlab上建立基于6个学习样本的RBF网络,通过不断调整隐含层节点数,即中心数,进行,选择扩展常数从0.2到20,步长为0.2的不同取值,进行优化网络。
例如,当中心数为5时,见图3。
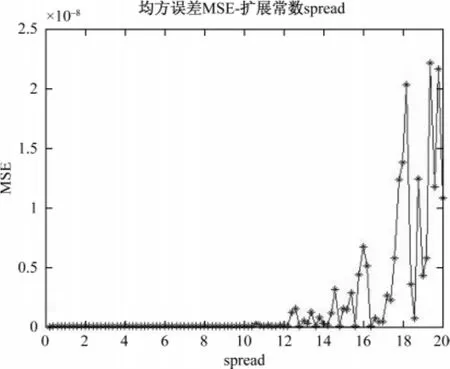
图3 不同扩展常数下的MSE变化趋势Fig.3 MSE trends under different extensions constant
由图3中可知,随着spread的增加,均方误差刚开始为零,随后在扩展常数为12以后发生波动,说明扩展常数并不是越大越好,由图中可见,此时的MSE在扩展常数0.2到12内都为0,说明此时的网络可以很好地反映输入和输出之间的关系。
由图4可知,SSE变化趋势与MSE变化趋势类似,这说明,网络精度和泛化能力都有不错的表现,针对已知样本具有很好的模拟能力。经Matlab计算,当扩展常数为7.4。
实际上由公式来看,MSE和SSE随着扩展常数的增加,理论上应该具有相似的趋势变化,以MSE为标准 (这里的零表示其数量级已经达到10-10或者更小),通过调整中心数,具体的仿真结果参见表3。
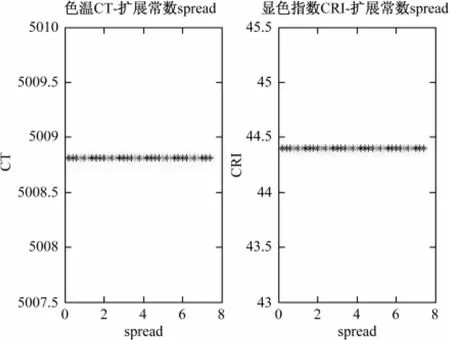
图4 不同扩展常数下的SSE变化趋势Fig.4 SSE trends under different extensions constant

表3 网络模型仿真结果Table 3 The simulation results of the network model
在表3中,显然随着中心个数的不断增加,RBF具有无限逼近的能力,输入和输出数据得到很好的模拟。同时从表中可以看出通过聚类方法,中心数为5或者6的网络模型,在MSE相同时,网络综合性能都很优异,不仅输出误差适中,而且扩展常数值符合常态,但对于这两种网络模型,通常情况下,RBF网络的设计在精度满足的情况下,会选取具有最小结构的神经网络[19]~[20],以保证神经网络的泛化能力,因此,本文最终选取第4个网络模型用于第6号样本的验证,见图5。
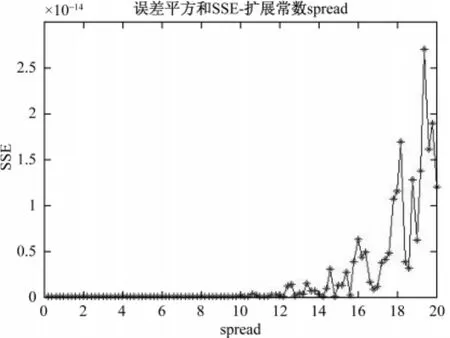
图5 不同扩展常数时的输出结果 (反归一化后)Fig.5 Results under different extensions constant
由图5可以看出,该网络模型针对测试样本6号输出结果与期望结果始终徘徊在个位数差值,尤其是显色指数方面,误差不超过0.5,与实际偏离值都在要求范围内,显示该网络模型的性能优越性,通过网络运行,此时的MSE在扩展常数为7.4时达到最小,数值为38.9,因此,最后确定扩展常数为7.4,结合7号样本进行预测,其结果见表4,此时中心个数为5,扩展常数为7.4。
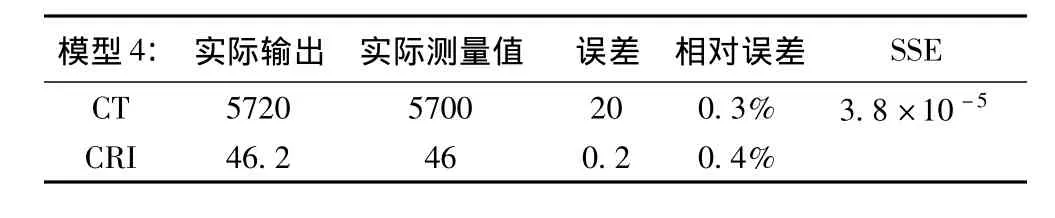
表4 第7号样本预测结果Table 4 No.7 prediction results
表4结果显示,该网络模型预测数据有效,表现在预测色温和实测数据仅相差20k,优越于飞利浦照明标准对产品色温的要求,同时显色指数偏离值只有0.2,相差值不超过1,符合输出结果要求。输出结果与测量值相对误差非常小,色温和显色指数的输出相对误差几乎一样;同时SSE精度很高,表现了该网络模型的泛化能力仍然具有很高的水平,因此该预测数据完全可以代替测量数据,省去测量步骤。采用该网络模型可以有效对三基色配比预测色温和显色指数,应用于光源的生产和评价。
4 结论
通过RBF神经网络建立的网络模型,采用聚类的方法,针对参照样本进行了学习和仿真,结果显示,该网络具有局部逼近的能力,只需三基色比例,就可同时获得理想的色温和显色指数,快捷有效。与传统的方法相比较,不仅简单实用,而且功能强大,可同时实现色温和显色指数的获得,对光源生产和及时有效的评价具有重要意义。
[1]Robertson A R. Computation of correlated color temperature and distribution temperature [J].J.Opt.Soc.Am.,1968,58(11):1528~1535.
[2]林岳,叶烈武,刘文杰等.二分法优化计算LED光源相关色温 [J].光学学报,2009,29(10):2791~2794.
[3]代彩红,于家琳,于靖等.颜色温度和相关色温的不确定度评定方法 [J].光学学报,2005,25(4):547~552.
[4]徐示波,吕毅军.陈焕庭等.基于二分法的RGB-LEDs配色研究 [J].光电技术应用,2009,24(6):7~10.
[5]张浩,徐海松.光源相关色温算法的比较研究.光学仪器,2006年2月.
[6]谭力,刘玉玲,余飞鸿.光源显色指数的计算方法研究.光学仪器,2004年8月.
[7]丘行中.光源显色指数计算的沃尔特方法改进 [J].照明,2000,(2):28~321.
[8]殷录桥,杨卫桥,李抒智,程备,张建华.基于三基色的动态色温白光发光二极管照明光源.光学学报,2011年5月,第31卷第5期.
[9]彭浩,刘东月,聂丛伟,茹志芹,黄杰.白光LED的显色指数模型研究.第十二届全国LED产业研讨与学术会议论文集,2010年.
[10]Buhmann M D. Radial Basis Functions:Theory and Implementations[M].Cambridge Univ.Press,2003:56~104.
[11]张雅,向虎,郭芳瑞.RBF网络模型参考自适应控制在温度控制中的仿真研究 [J].系统仿真学报,2008,28(2):429~432.
[12]陈琪.基于RBF的语音情感识别方法的研究.硕士论文,长沙理工大学,2010年3月.
[13]李彬.径向基函数神经网络的学习算法研究.硕士论文,2005年4月,山东大学.
[14]刘文菊,郭景.RBF神经网络中心选取OLS算法的研究 [J].天津工业大学学报,2002,21(2):71~73.
[15]王红萍,金彦丰,曹海军,陈晓辉.基于径向基函数网络的水声信号预测模型研究.舰船电子工程,2008年第10期.
[16]CIE Technical Report 177:2007.Color rendering of white LED light sources.ISBN 9783901906572.
[17]Wendy Davis,Yoshi Ohno.Towards an improved color rendering metric.Proc.of SPIE Vol.5941 59411G.
[18]Artūrasukauskas, Rimantas Vaicekauskas, Michael Shur.Solid-state lamps with optimized color saturation ability,OPTICSEXPRESS,2010,Vol.18,No.3.
[19]Niyogo P, Gorisi F. On the Relationship between Generalization Error,Hypothesis Complexity and Sample Complexity for Radial BasisFunction [J]. Neural Computation,1996(8):819~842.
[20]Moody J.The Effective Number of Parameters:A Analysis of Generalization and Regularization in Nonlinear Learning System [J].NIPS4,1992:847~854.
