分布式多天线信道时变特征参数的联合估计

张静

(上海师范大学 信息与机电工程学院，上海 200234)

1 引言

在收发端配置多根天线的多天线系统即多输入多输出(MIMO)系统可以有效地利用空间分集并改善链路的可靠性。利用分散在不同地点的无线终端构成分布式MIMO系统在协同通信乃至多点协作重传等技术中被广泛采纳。由于无线移动终端分布地点分散，组成虚拟MIMO系统时在接收端得到的是包含多个不同的信道状态信息：衰落、时延和频率偏置这3类特征参数的混叠信号。准确地获取这些参数并进行有效的同步和均衡，可显著地改善接收机性能。

在分布式MIMO系统中，当多个频率偏置和平信道衰落在多个符号周期不变时，参数的联合获取可采用期望最大化方法，它避免了极大似然估计的求逆运算，可逼近参数的克拉默—拉奥下界[1]，还可运用最小二乘估计和最小均方误差估计[1～3]；对时变特征参数的获取有以下几种方法：建立MIMO信道的状态空间模型，用卡尔曼滤波来跟踪参数[4]；用序列蒙特卡洛方法获取在伪码辅助下的信道衰落[5]。此外，将时变信道近似为在若干个符号周期不变，以及联合估计MIMO-OFDM系统的信道衰落和频率偏置[6]及盲方法等[7]。

本文针对多天线无线信道随机时变的特点，考虑分布式MIMO系统时变特征参数的联合获取。它包括多个复信道衰落和多个频率偏置的联合估计。依据无线信道的统计模型理论建立了参数的状态空间模型，对强非线性观测模型进行线性化处理，然后运用扩展卡尔曼滤波算法联合获取多个未知参数，同时将结果对照了参数估计的克拉默—拉奥下界。

2 接收信号模型及其线性化

一个具有NT根发送天线和NR根接收天线的分布式MIMO传输系统如图1所示。对分布式的NT个发送天线上的发送符号{x1,x2,…,xNT}进行空时编码得到在时刻k的发送符号{s1(k),s2(k),…,sNT(k)}，在发送符号中插入导频序列，然后经由无线信道传输。在第r个接收天线上的接收信号为

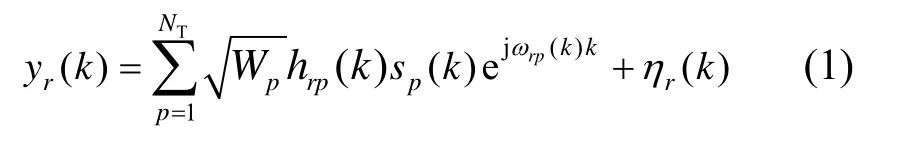
其中，Wp为第p个发送天线的发射功率，hrp(k)为第p个发送天线和第r个接收天线间在时刻k的复信道衰落，sp(k)为时刻k在第p个发送天线上的发送符号，ωrp(k)=2πfrp(k)Ts为归一化后的载波频率偏置，其中，frp(k)为时刻k的绝对实际频偏，Ts为符号周期；0＜ωrp(k)＜π，ηr(k)为均值为0、实部和虚部的功率为N02/2的复高斯观测噪声。

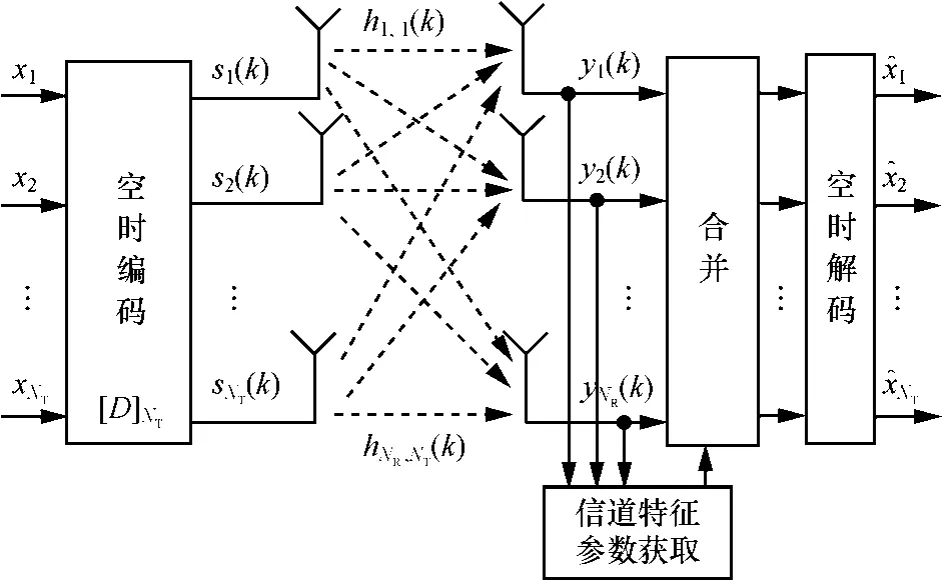
图1 分布式MIMO系统传输模型

因参数估计过程在所有的接收天线上相同，不失一般性，略去下标r。式(1)在导频点处的接收信号为

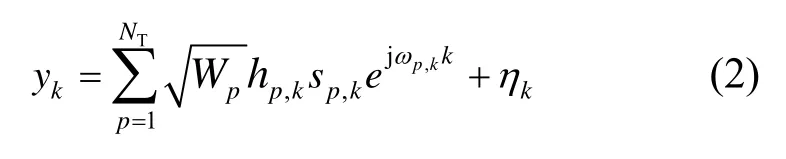
设导频序列每隔若干个由发送符号构成的空时编码块后插入且接收端已知，此时式(2)包含和这些未知参数。由于该非线性观测模型的未知参数为时变参数且混叠在接收信号中，获得解析解较困难。当采用足够小的采样间隔时，可利用扩展卡尔曼滤波进行参数获取。为此对式(2)进行线性化。记式(2)为yk=f(xk)+ηk，其中，将yk在状态估计值附近展开成泰勒级数，并取其一次项，有

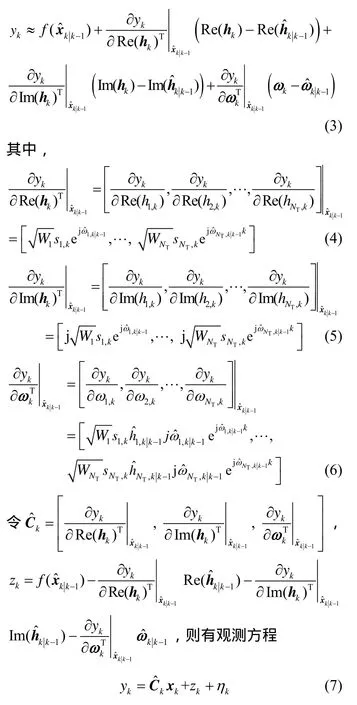
3 时变信道特征参数的状态空间模型

上述分布式MIMO系统的发射天线共时共频传送信息对接收端信号造成了混叠。在发送天线不相关时，多根发送天线和某个接收天线间构成了独立的多径信号。对于小尺度衰落，当接收机带宽B和符号周期Ts一定时，每条主路径可用信道衰落、频偏、时延3类特征参数{hp,fp,τp}的亚扩展函数来表征，其等同于若干个不可分辨的时延小于1/2B并且频偏小于1/2Ts的路径的和[8]。hp的幅值在无直射波时服从瑞利分布，相位服从(0,2π]间的均匀分布。更进一步地，可将时延和信道衰落用直角坐标方式表示为复信道衰落，时延等效为复信道衰落的相位。然后建立参数化的二阶自回归模型[4]

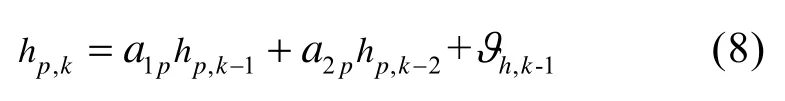
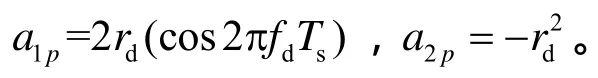
其中，其中，df是最大的多普勒频移，dr是信道功率时延谱的衰减系数，

频率偏置为慢变参数，可建立为一阶自回归模型

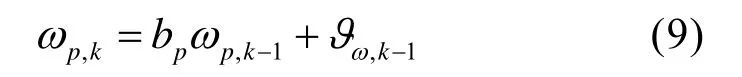
其中，pb为与移动速度有关的系数，

将式(7)、式(8)表示成状态空间模型为

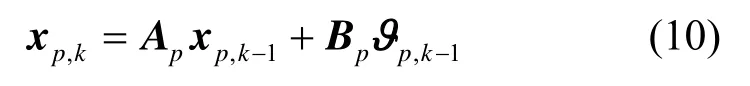
将所有发送天线对任一根接收天线间信道特征参数的状态方程表示为

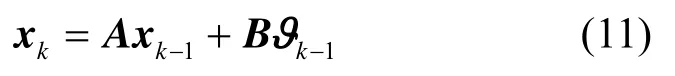
4 扩展卡尔曼滤波（EKF）算法

4.1 EKF算法

EKF算法在过程噪声和观测噪声均为高斯白噪声时具有最优意义。当对过程模型和观测模型线性化后，EKF公式与常规卡尔曼滤波公式一致。针对式(6)和式(10)的模型，在设定初始状态x0、初始估计误差方差P0以及过程噪声方差1k-Q和观测噪声方差kR后，可进行如下计算获得每步EKF估计值和估计误差方差kP，即有

1) 一步预测

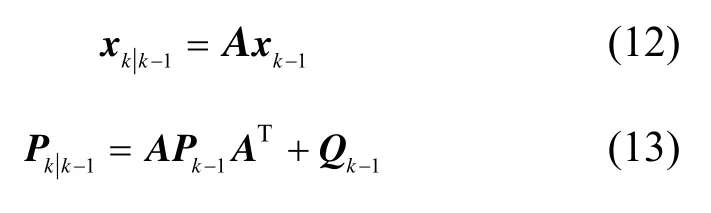
2) 一步修正因子

3) 一步修正估计误差方差

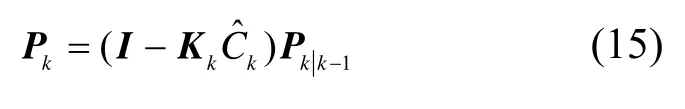
4) 一步修正

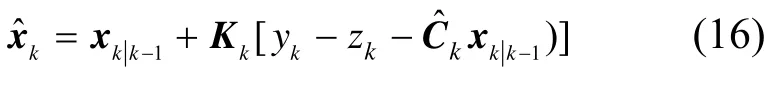
4.2 时变特征参数估计的克拉默—拉奥下界

根据文献[9]，该模型下参数估计的克拉默—拉奥下界为递推费希尔矩阵kJ的逆。kJ为

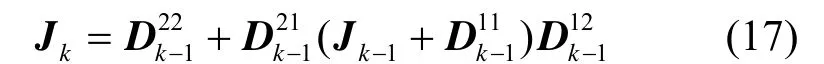
5 仿真实例

本文仿真考察时变信道参数联合估计性能。不失一般性，考虑2发1收分布式MIMO系统时变复信道衰落和时变频率偏置的联合估计，并设MIMO信道的各子信道为瑞利衰落信道。仿真参数的数值见表1。

本文进行了三方面的仿真，一是在给定的信噪比条件下考察联合估计时参数的均方误差(MSE)随观测值个数增加而变化的情况；二是当估计收敛后各参数的MSE随信噪比的变化情况；三是考察过程噪声对MSE的影响。通过与参数的克拉默—拉奥下界（CRLB）对比来进一步表明参数的估计性能。

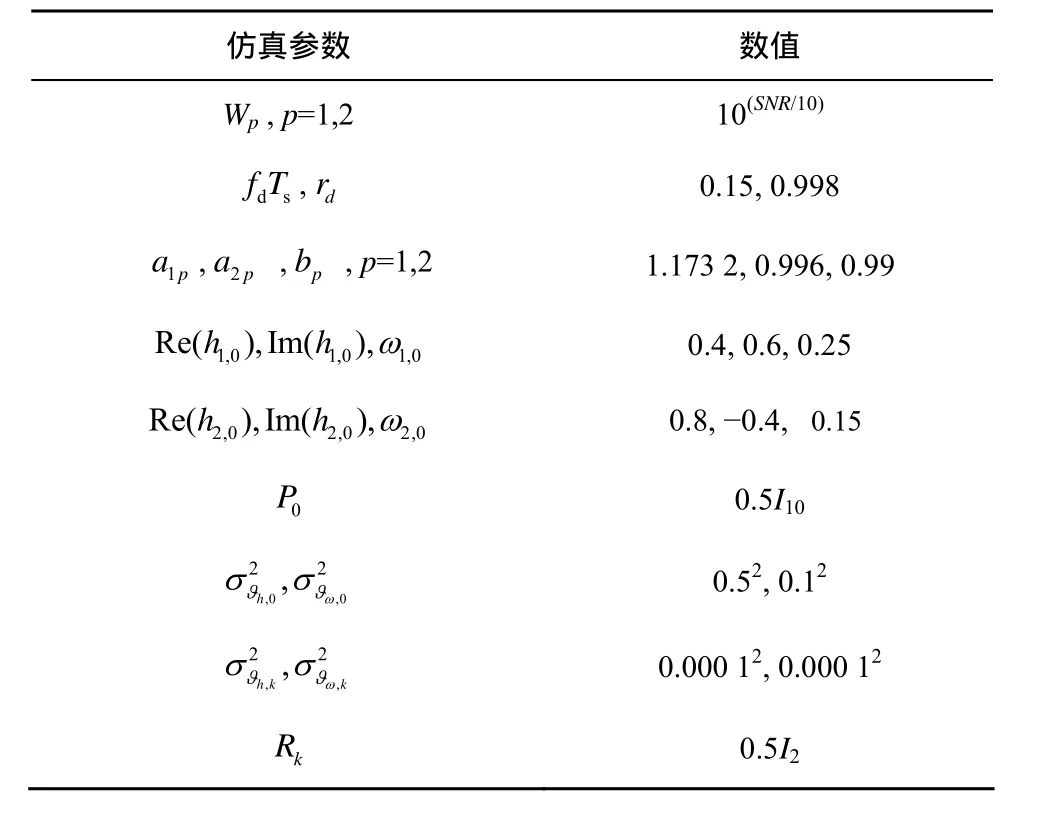
表1 仿真参数数值

图2是在设定信噪比（SNR）为0dB时，由EKF估计的信道衰落h1实部的MSE与CRLB随观测值个数增加而变化的曲线。其他信道衰落参数具有与该图类似的估计情况，不再示出。图3是由EKF估计的频率偏置1ω的MSE与CRLB随观测值个数变化的曲线。这2幅仿真曲线表明，EKF估计的MSE和CRLB都随观测值个数的增加渐近收敛，在观测值个数达到10时，EKF估计的MSE已可进入稳态。同时，由于信道衰落模型被建立为二阶AR正弦振荡模型，导致CRLB和EKF估计值在稳态时都具有类似正弦的振荡形式，且EKF的MSE接近CRLB。

图4和图5是在EKF和CRLB均已进入稳态后，在第40个观测时刻EKF的MSE随SNR的变化曲线。仿真结果表明，EKF的MSE随SNR的增加逐渐减小，稳态时与CRLB相当。

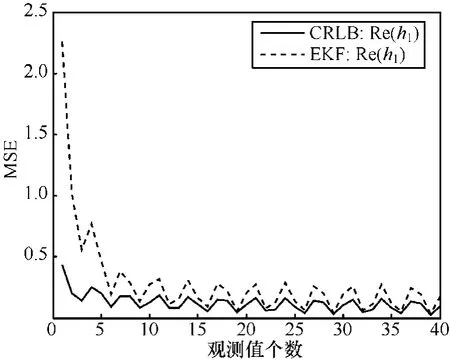
图2 信道衰落估计的渐近收敛曲线与CRLB曲线

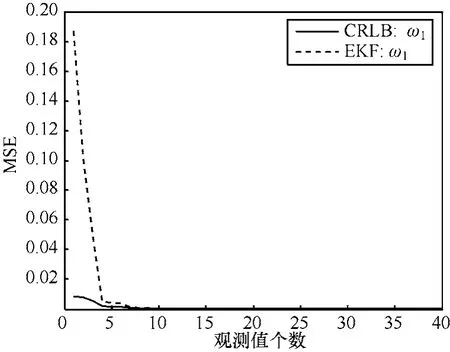
图3 频率偏置估计的渐近收敛曲线与CRLB曲线

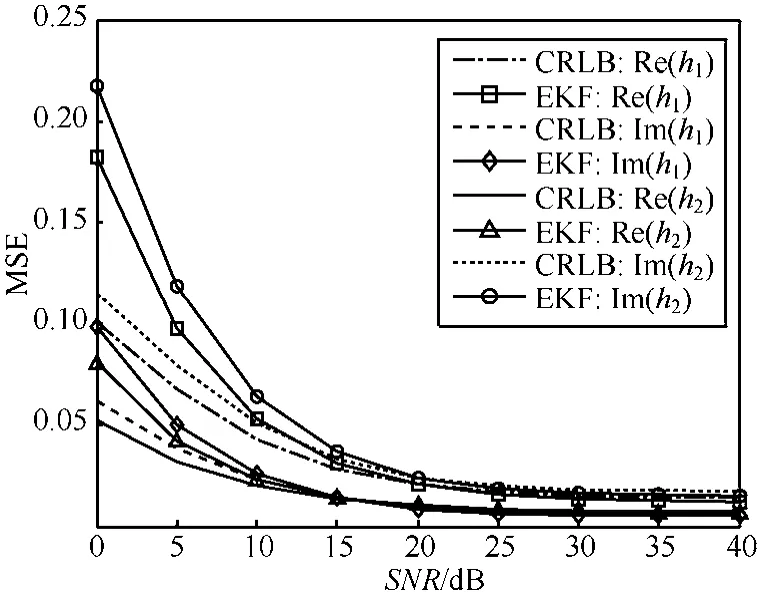
图4 信道衰落估计与CRLB曲线

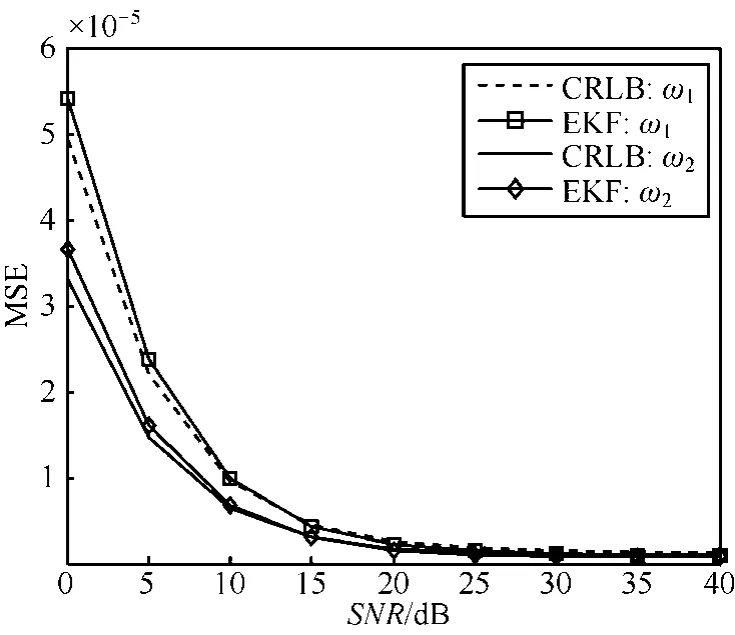
图5 频率偏置估计与CRLB曲线

图6和图7是在SNR为0dB时，各参数估计值随过程噪声方差的数量级而变化的曲线。这些曲线表明，当过程噪声方差小于10-6时，参数能良好地估计，但是随着方差数量级的增加，各参数的MSE迅速增大。

这些仿真结果表明，当分布式多天线信道随机时变特征参数的方差较小即过程噪声方差较小时，EKF联合估计到达稳态所需的导频数目以及稳态估计精度与参数时不变时极大似然估计的情况相当[1]，MSE收敛速度较快，估计精度可逼近CRLB。但是，当特征参数的方差较大时，由于各特征参数耦合在观测模型中，联合估计时各参数的估计过程有较大程度的互相影响，加上频率偏置的观测模型呈现较强的非线性，EKF联合估计还存在MSE较大的不足。此外，由于分布式多天线信道是典型的随机时变信道，其时不变参数可视作方差为零的随机参数的特例，因此，可运用EKF联合估计既包括静止终端也包括移动终端之间信道的特征参数，适用性较为广泛。

图6 信道衰落估计的MSE随过程噪声阶次的变化曲线

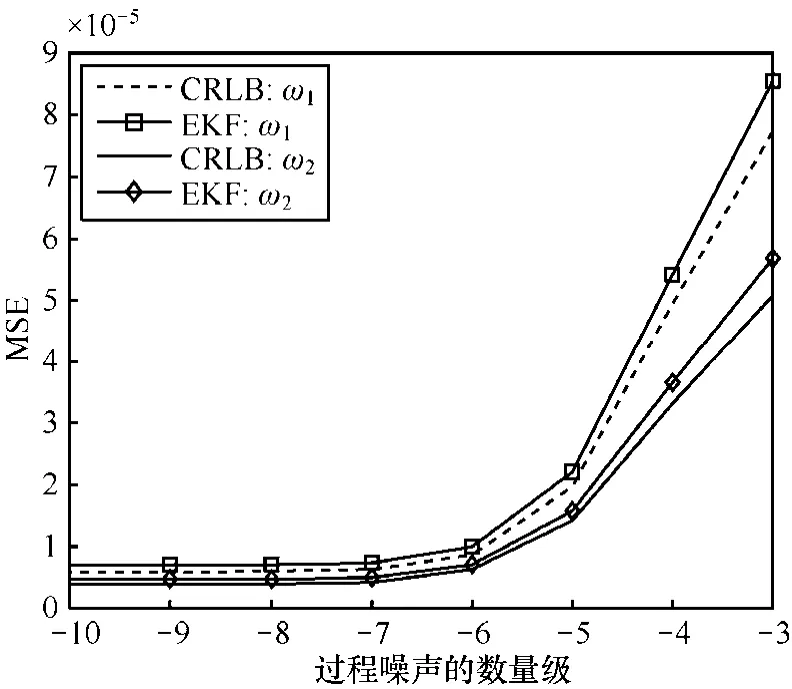
图7 频率偏置估计的MSE随过程噪声阶次的变化曲线

对比仿真结果中频率偏置和复信道衰落的估计性能曲线还可以看出，频率偏置的MSE收敛曲线为线性，稳态时的MSE很小；而复信道衰落的MSE收敛曲线为振荡形式，稳态时的MSE较大。这一方面是由于频率偏置是一阶慢变参数而复信道衰落是二阶快变参数，另一方面是由于频率偏置和复信道衰落对观测信号的影响情况不同。时变的频率偏置使观测信号产生时变相移，该相移基本不受复信道衰落及其时变性的影响，在SNR较低时就可使频率偏置估计的MSE很小，但该相移会改变复信道衰落在2个正交支路上的观测信号，从而导致复信道衰落估计的MSE较大。

6 结束语

本文考虑分布式多天线信道的特征参数：复衰落和频率偏置为随机时变参数，运用了扩展卡尔曼滤波来联合估计。它建立各参数的自回归及状态空间模型，求解观测方程的雅可比矩阵进而线性化观测方程，再通过序贯的观测值估计参数。这种联合获取方法在特征参数的方差较小时，估计跟踪精度可逼近克拉默—拉奥下界，到达稳态时所需的导频数目与对时不变特征参数做联合最优估计时所需的导频数目相当，具有较广泛的适用性。

[1] PHAM T H, NALLANATHAN A, LIANG Y C. Joint channel and frequency offset estimation in distributed MIMO flat-fading channels[J]. IEEE Trans Wireless Communication, 2008, 7(2):648-656.

[2] NOORALIZADEH H, MOGHADDAM S S. A novel shifted type of SLS estimator for estimation of Rician flat fading MIMO channels[J].2010, 90(6):1886-1893.

[3] ROSSI P S, MULLER R R. EDFORS O. Linear MMSE estimation of time–frequency variant channels for MIMO-OFDM systems[J]. Signal Processing, 2011, 91(5):1157-1167.

[4] ENESCU M, ROMAN T, KOIVUNEN V. State-space approach to spatially correlated MIMO OFDM channel estimation[J]. Signal Processing, 2007, 87(9): 2272-2279.

[5] VAZQUEZ M A, BUGALLO M F, MIGUEZ J. Sequential monte carlo methods for complexity-constrained MAP equalization of dispersive MIMO channels[J]. Signal Processing, 2008, 88(4):1017-1034.

[6] AMO C P D, JIMÉNEZ V P G, GARCÍA M J F G. Joint channel and frequency offset estimation in MIMO-OFDM systems with insufficient cyclic prefix[J]. Physical Communication, 2011, 6(22): 254-265.

[7] PALAMIDES A, MARAS A, VELONI A, etal. Blind tracking of channel state and multiple frequency offsets in MIMO–OFDM systems[J]. Physical Communication, 2011, 4(2):123-126.

[8] GIANNAKIS G B, HUA Y B, STOICA P, etal. Signal Processing Advances in Wireless and Mobile Communications, volume 2: Trends in Single-and Multi-User Systems[M]. Beijing: Post and Telecom Press, 2002. 403-433.

[9] LEI M, VAN WYK B J, QI Y. Online estimation of the approximate posterior Cramer-Rao lower bound for discrete-time nonlinear filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011,47(1):37-57.