一类求解堆石混凝土结构温度场分布的解析法

麦 戈，唐欣薇，唐照平

（1.仲恺农业工程学院城市建设学院，广州 510225；2.华南理工大学亚热带建筑科学国家重点实验室，广州 510640；3.中交第三航务工程勘察设计院有限公司，上海 200032）

一类求解堆石混凝土结构温度场分布的解析法

麦 戈1，唐欣薇2，唐照平3

（1.仲恺农业工程学院城市建设学院，广州 510225；2.华南理工大学亚热带建筑科学国家重点实验室，广州 510640；3.中交第三航务工程勘察设计院有限公司，上海 200032）

堆石混凝土作为一种新型材料已应用于水利、港口、采矿等诸多工程结构，目前，对于这种材料的应用仍处于发展阶段。为深入研究堆石混凝土的热力学特性，根据堆石混凝土结构的特性，建立等效的计算模型，确定堆石混凝土温度场的数理方程，并获得材料温度场分布的解析解。以一个堆石混凝土结构为例，借助Matlab的编程工具，分析了温度变化特性。计算实例表明，该解析法可用于研究堆石混凝土材料温度场的分布规律，为研究堆石混凝土材料的温度场变化奠定了理论基础。

堆石混凝土；温度场；数理方程；解析解

1 研究背景

堆石混凝土是将大粒径的块石直接堆放入仓，然后从堆石体的表面浇筑无需任何振捣的专用自密实混凝土，并利用专用自密实混凝土高流动性、高穿透性的特点，依靠自重完全填充堆石的空隙，形成完整、密实、水化热低、满足强度要求的大体积混凝土。

堆石混凝土的施工技术与方法于2003年获得了国家专利［1－2］，安雪晖等［3－6］针对这一新型材料开展了基本力学试验研究。这一新型复合材料与普通混凝土相比，具有水泥用量较少，水化热温升较低，施工时连续抛石铺填、连续灌注自密实混凝土，无需碾压或振捣，可减少人工结构缝与施工缝，因而加快了施工建设进程，降低造价。

根据堆石混凝土的特性，不仅可将其推广应用在堆石混凝土拱坝、重力坝、心墙堆石坝和堆石混合坝等大坝结构形式中，也可将其应用在围堰、港口、海工、护坡、块石胶结充填采矿等结构形式中，其应用前景广阔，目前已在京郊西山试验坝中获得初步成功，此外，还应用于河南宝泉抽水蓄能电站副坝、四川宜宾向家坝水电站沉井回填等工程中［7－8］。

目前，采用这一复合材料建坝存在的主要问题是：针对堆石混凝土的各种综合性能比如弹性模量、收缩性能、绝热温升等还需要进一步研究；并且针对堆石混凝土技术的施工工艺同样需要作进一步研究，以便对其进行优化，建立更加完备的堆石混凝土施工方法。因此，这一新型材料应用仍处于发展阶段。

本文立足于堆石混凝土的结构特征，建立合理的数理方程，对堆石混凝土结构温度场的解析解进行求解，为研究堆石混凝土的温度场变化规律奠定理论基础。

2 问题描述

为了定性地研究堆石自密实混凝土结构的温度场分布规律，可以将其近似简化成图1的形式求解热传导问题，其中区域1代表堆石体，可视为散热材料；区域2代表自密实混凝土，可产生水化热，引起自密实混凝土温升。根据该结构及其材料的特点，

图1 求解示意图Fig.1 Sketch of simplified rockfill concrete for solution

可得到以下求解方程及约束条件：

热传导方程：

式中：k为导温系数；β为放热系数；q为导热系数；u0为年平均气温；ur为堆石体的初始温度；us为自密实混凝土的初始温度；θ0为自密实混凝土的初始水化热。

3 热传导偏微分方程的求解

本文采用参数的下标和区域编号一一对应。求解过程主要分3步。

（1）步骤1：求解使边界条件齐次化的特解。

设u（r，t）＝v（r，t）＋w（r，t），其中w（r，t）为满足方程和边界条件的特解。为了使边界条件的齐次化，并考虑到t→∞，u1（r，∞）＝u0，可令w1＝u0。则初始条件可记为：v1（r，0）＝u1（r，0）－w1（r，0），即v1（r，0）＝ur－u0。同理可令：w2（r，t）＝u0，则

v2（r，0）＝u2（r，0）－w2（r，0） 。

即v2（r，0）＝us－u0。

（2）步骤2：利用分离变量法，求解齐次方程的本征函数。

将v2（r，t）＝u2（r，t）－u0代入式（5），必然得到齐次化的边界条件，即

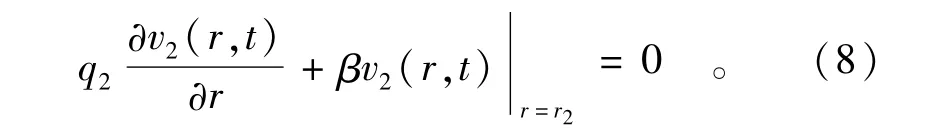
由于式（2）含有非齐次项，因此可以先求齐次方程、齐次边界条件的一般解为

采用分离变量的方法，即令v（r，t）＝R（r）T（t），对应的本征值为β2。对于每一个本征值β2n，通过方程和边界条件，都可以确定出相应的Rn（r）及Tn（t）。由于偏微分方程和边界条件都是齐次的，把它们（任意有限）的特解叠加起来，只要级数具有一定的收敛性，便可以得到合理的一般解［9］，即v（r，t）＝

式（12），式（13）含An，Bn，βn3个未知数，结合方程的边界条件和连接条件可得：

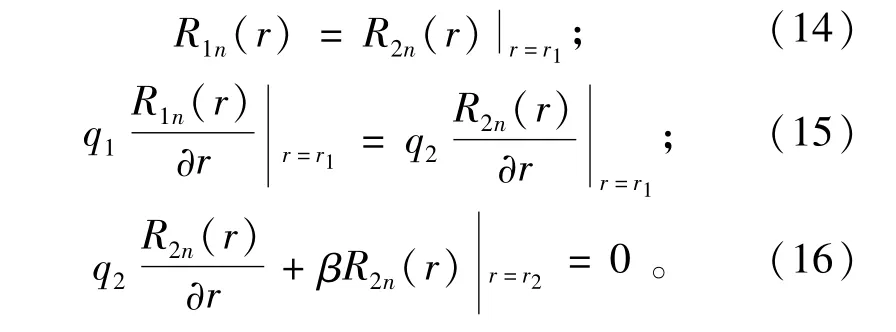
联立式（14）至式（16）可以得到以上3个未知数。即

其中：

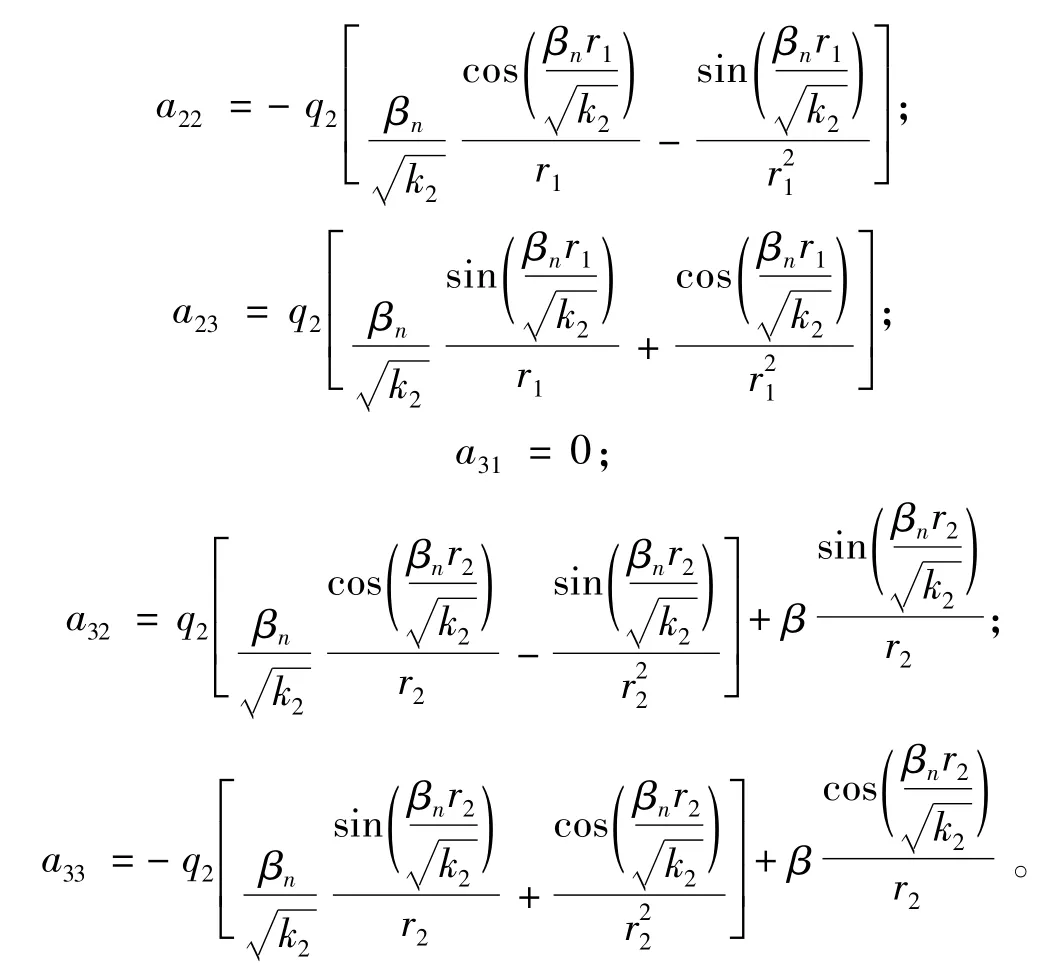
由矩阵行列式为0，可以确定βn，再将βn代入式（17）得到

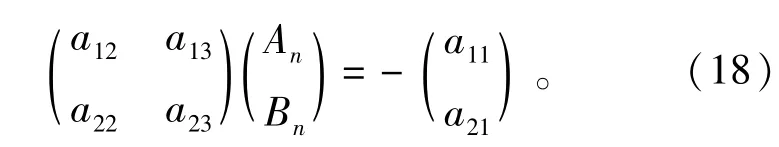
由式（18）可解得系数An，Bn。则齐次问题的求解基本完成，可以得到相应的关于径向r的本征函数组以及本征值。所求问题的解的形式为

（3）步骤3：将方程非齐次项及初始条件按本征函数展开，并最终得到方程的解。

对于式（2）的非齐次项，可以用齐次方程的本征函数展开，即

式中Rn具备正交函数的性质［10］，根据正交函数的性质，可得展开系数为

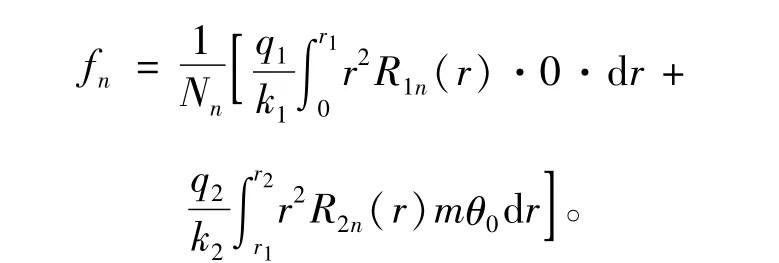
归一化系数为

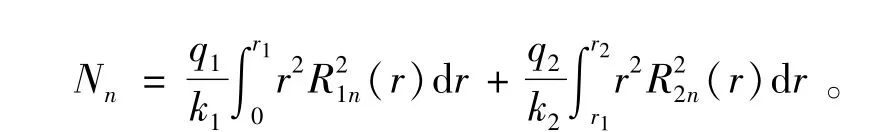
同理把初始条件按本征函数组展开得

利用正交函数的性质，可求得展开系数为

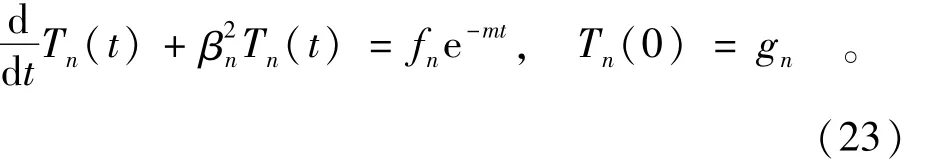
考虑到Tn＝A e－β2nt＋B e－mt（第一项是通解，第二项是特解），代入式（23）可得

综上，可以得到式（1），式（2）在式（3）至式（7）约束条件下的最终解，即

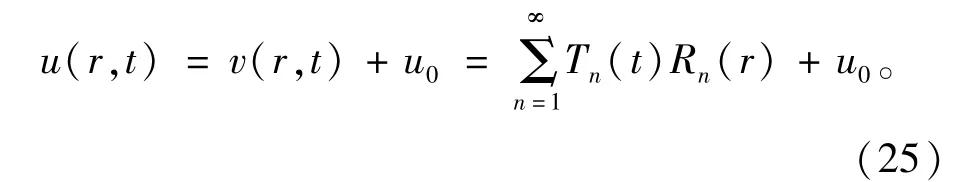
式（25）即为本文给出的堆石混凝土温度场分布的显式解析表达式，在实际计算时，在给定了材料属性后，利用Matlab软件进行编程，依次对各待定系数及温度场进行求解计算。

4 算例分析

为分析堆石混凝土材料温度变化的规律，本文取一组堆石混凝土为算例，堆石体及自密实混凝土的计算参数如表1所示；温度条件为：年平均气温u0＝20℃，堆石体初始温度ur＝4℃，自密实混凝土初始温度us＝15℃。自密实混凝土的水化热温升方程为θ＝24.0（1－e－0.09t）。计算时间取300 d，时步为1 d。计算结果如图2和图3所示。

堆石体以较低温度（4℃）投放，堆石体外部被自密实混凝土包围，而自密实混凝土产生水化热，使得堆石体温度不断升高。从图2中可以看出，越靠近外部的自密实混凝土（r越大），堆石体的温度提高得越快，最终形成稳定的温度场。

表1 堆石体及自密实混凝土计算参数Table 1 Calculation parameters for rockfill and self—compacting concrete

图2 堆石体内部温度场变化Fig.2 Variation of temperature field inside the rockfill

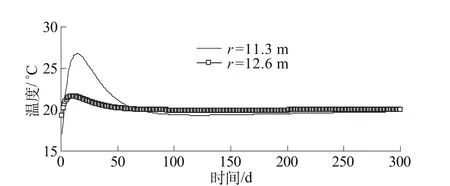
图3 自密实混凝土内部温度场变化Fig.3 Variation of tem perature field inside the self compacting concrete

由图3可知，在自密实混凝土内部，由于受外部气温及堆石体的影响较小，水化反应引起温度的升高（从20℃增加到26.78℃），随着混凝土表面的不断散热，温度场趋于稳定（r＝11.3 m）。而自密实混凝土的表面（r＝12.6 m）受外界气温影响较大，绝热温升幅度不大（从20℃增加到21.63℃），并随着表面的不断散热，温度场趋于稳定（与外界多年平均气温相近）。

5 结 语

针对堆石混凝土材料的自身特点，本文建立了等效的计算模型，确定了堆石混凝土温度场分布的数理方程，并给出了温度场分布的显式解析表达式。以一个堆石混凝土结构为例，借助Matlab的编程工具，研究了堆石混凝土材料温度场的分布规律，并最终形成稳定的温度场，该成果为堆石混凝土材料温度场变化的研究奠定了理论基础。

［1］ 金 峰，安雪晖.堆石混凝土大坝施工方法：中国，30102674.5［P］.2003.（JIN Feng，AN Xue hui.Con struction Method for Rock Fill Concrete Dam：China，30102674.5［P］.2003.（in Chinese））

［2］ 金 峰，安雪晖，石建军，等.堆石混凝土及堆石混凝土大坝［J］.水利学报，2005，36（11）：1347－1352.（JIN Feng，AN Xue hui，SHI Jian jun，et al.Study on Rock fill Concrete Dam［J］.Journal of Hydrau lic Engineering，2005，36（11）：1347－1352.（in Chi nese））

［3］ 安雪晖，金 峰，石建军.自密实混凝土充填堆石体的试验研究［J］.混凝土，2005，10（1）：3－6.（AN Xue hui，JIN Feng，SHIJian jun.Experimental Study of Self compacting Concrete Filled Prepacked Rock［J］.Concrete，2005，10（1）：3－6.（in Chinese））

［4］ 石建军，张志恒，金 峰，等.自密实混凝土充填堆石体的试验［J］.南华大学学报，2005，19（1）：38－41.（SHI Jian jun，ZHANG Zhi heng，JIN Feng，et al.Experiment on Self compacting Concrete Filling Rock fill［J］.Journal of University of South China，2005，19（1）：38－41.（in Chinese））

［5］ 周 虎，安雪晖，金 峰.低水泥用量自密实混凝土配合比设计试验研究［J］.混凝土，2005，10（1）：20－23.（ZHOU Hu，AN Xue hui，JIN Feng.Experi mental Study of Low Cement Dosage Self compacting Con crete Mix Design［J］.Concrete，2005，10（1）：20－23.（in Chinese））

［6］ 周绍青，石建军，杨晓峰，等.神经网络在自密实混凝土流动性能中的应用［J］.水利与建筑工程学报，2005，3（4）：42－45.（ZHOU Shao qing，SHI Jian jun，YANG Xiao feng，etal.Application of Neural Network in Prediction for Flowing Property of Self compacting Con crete［J］.Journal of Water Resources and Architectural Engineering，2005，3（4）：42－45.（in Chinese））

［7］ 宋殿海，刘 剑.自密实堆石混凝土在宝泉抽水蓄能电站的应用［J］.水力发电，2007，33（9）：26－28.（SONG Dian hai，LIU Jian.Application of Self compac ted Rockfill Concrete in Baoquan Pumped Storage Power Station［J］.Water Power，2007，33（9）：26－28.（in Chinese））

［8］ 安雪晖，黄绵松，周 虎，等.堆石混凝土施工技术综述［C］∥全国混凝土新技术及其工程应用技术交流会.中国：宁波，2007：23－31.（AN Xue hui，HUANG Mian song，ZHOU Hu，et al.Review of Construction Technology for Rock Fill Concrete［C］∥National Sympo sium on New Concrete Technique and Its Engineering Ap plication.Ningbo，China，2007：23－31.（in Chinese））

［9］ 吴崇试.数学物理方法［M］.北京：北京大学出版社，1999.（WU Chong shi.Methods of Mathematical Physics［M］.Beijing：Peking University Press，1999.（in Chi nese））

［10］M.N.奥齐西克.热传导［M］.俞昌铭，译.北京：高等教育出版社，1983.（OZISIK M N.Thermal Conduc tion［M］.Translated by YU Chang ming.Beijing：High er Education Press，1983.（in Chinese） ）

（编辑：黄 玲）

An Analytical M ethod for Tem perature Field Distribution of Rock fill Concrete Structure

MAIGe1，TANG Xin wei2，TANG Zhao ping3
（1.School of Urban Construction，Zhongkai University of Agriculture and Engineering，Guangzhou 510225，China；2.State Key Laboratory of Subtropical Building Science，South China University of Technology，Guangzhou 510640，China；3.CCCC Third Harbor Consultants Co.，Ltd.，Shanghai 200032，China）

As a new typematerial，RFC（rock fill concrete）has been applied to structures of hydraulic engineering，harbor engineering and mining engineering.At present，the application of RFC is still in the stage of development.To research the thermodynamic properties，an equivalentmodel is built according to characters of RFC structure.Themathematical equation for the temperature field of RFC is constructed，and the analytical solution of tempera ture field distribution is obtained.Taking an RFC structure as an example，Matlab is used as a programming tool to analyze the temperature properties of the structure.Results show that the analyticalmethod in this research could be used to study the temperature field distribution of RFC.It lays a theoretical foundation for the study of RFC temper ature field.

rock fill concrete；temperature field；mathematical equation；analytical solution

TU 37

A

1001－5485（2013）12－0097－04

10.3969／j.issn.1001－5485.2013.12.018 2013，30（12）：97－100，106

2012－11－28；

2013－01－23

国家自然科学基金青年基金（51109083）；中央高校基本科研业务费专项资金（2012ZM0091）；华南理工大学亚热带建筑科学国家重点实验室开放基金（2011KB28）

麦 戈（1970－），女，广东广州人，高级工程师，主要从事土木工程、环境工程的研究，（电话）13660215386（电子信箱）maige8821＠163.com。