回转装置内三组元颗粒径向混合评价方法分析

李少华，朱明亮，张立栋，王 擎，刘朝青，于丁一

（1 中国大唐科学技术研究院，北京 100032；2 东北电力大学油页岩综合利用教育部工程研究中心，吉林 吉林 132012）

混合是物料在外力（重力或机械力等）作用下发生运动速度和运动方向的改变，使各组分颗粒均匀分布的操作过程；其目的在于通过混合过程获得组成和性质均匀的混合物，以保证所得产物组成、结构和性能的均匀一致性[1-2]。

国内外对颗粒混合的研究从20 世纪中叶开始至今一直没有停息过。1966年Hogg 等[3]对水平搅拌混合装置进行实验研究并提出了混合动力方程；李水清等[4-5]利用分子动力学在中等转速情况下经受力分析模拟颗粒在水平回转设备中的运动轨迹，并用PIV 试验进行验证。Ottino 小组[6-8]对颗粒物料的混合与分离进行了基本阐述，并提出建立颗粒物料运动模型所需考虑的基本问题与颗粒混合计算方法，通过实验对EDEM 等模拟软件的模拟结果进行论证。Jha 等[9]研究了不同应变速率物料对混合的影响，并得到当应变速率为0.25 与0.5 时二元物料混合最好。Cleary 等[10]采用DEM 方法模拟了滚筒中的颗粒混合，并采用了两种不同方法估算混合度。Simo Siiriä 等[11]采用DEM 方法研究混合参数的选择对混合效果的影响，得出选择合适的混合参数，不但提高了混合的最终效果，而且在减少混合器耗损上也有着良好的效果。赵永志等[12-14]对薄滚筒内二元S 型颗粒体系采用DEM 方法对颗粒流动进行数值模拟，讨论颗粒在薄滚筒内混合、运动及分布情况。

在这些研究中，颗粒混合度的评价一直没有一个定性的分析，虽然各学者均采用与自己研究相适合的混合度评价方式，但并无具体分析。本文作者以回转装置内三组元颗粒径向混合实验为研究背景，对比较常用的混合度评价方法进行简单介绍与 对比，并针对Lacey 指数取样及计算相关问题进行探讨。

1 混合度评价方法简述

混合作为一个颗粒与颗粒间的物理行为，其混合过程极其复杂，对其混合程度的描述也难以详尽。通常以定性描述的方式评价混合度，比较其混合优劣。图1 是经常被用来描述颗粒的3 种混合状态。图1(a)为完全分离状态，又称为颗粒混合初始状态；图1(b)为部分混合状态，又称为随机混合状态，一般实际混合状态就是这一状态，两种颗粒呈无序不规则排列方式；图1(c)为完全混合状态，又称为理想混合状态，两种颗粒完全均匀地分布在一个颗粒群里，且互相之间接触最大而同种颗粒间无接触，但这种状态一般在生产中无法达到。

为了能够定量的分析颗粒间的混合程度，以便直观地了解其混合程度的高低，通常采用标准差、 变异系数、接触数、混合指数等来评价混合程度。

图1 颗粒混合模型

1.1 标准差评价法

该方法主要利用多组样本数据的标准偏差σ 来评价颗粒混合程度，是一种较为简单的评价方法，但标准偏差的大小与测定次数有关。另外，标准偏差值与各测定值相对于平均值的残差有关，而与各测定值本身的大小无关。当混合物料中的组分含量相差悬殊时，用标准偏差很难说明混合程度。因此仅用标准偏差还不足以充分说明混合程度。

1.2 变异系数评价法

变异系数（Cv）又称离散度，为了客观地反映混合程度，在上述标准偏差方法的基础上对平均值这一参数突显出来，用以弥补标准偏差法的不足。其算法为在上述标准偏差的基础上再利用式（1）进行计算。

变异系数能够较客观地反映出颗粒混合情况，曾被应用于测量回转装置内颗粒轴向混合度[15]。但对于径向混合来说，如果对混合各时刻图像进行网格取样，计算所得混合受局部影响很大，如本实验混合稳定后利用变异系数法计算得52 s 时Cv=1.6，而在54 s 时Cv=0.874，其值变化极大，不能够正确地反映出径向混合变化规律。

1.3 接触数评价法

Van Puyvelde 等[16]通过对颗粒混合图像的研究提出了通过计算颗粒接触数来衡量颗粒混合程度的方法，这种方法能计算出不同区域内的混合程度。由图1 可以得出，(a)接触数为5，(b)接触数为23，(c)接触数为31，通过这组接触数可以很好地反映出不同时刻特定区域内颗粒的混合状态，在区域(a)、(b)、(c)内接触数有很大的区别，颗粒接触数呈现出递增的趋势，混合度也呈现出递增的趋势，采用接触数评价混合度能很好地反应混合程度。

张立栋等[17]采用大颗粒和小颗粒之间的接触数与总的接触数（大颗粒与大颗粒，大颗粒与小颗粒，小颗粒与小颗粒）的比值来衡量混合程度q，其数学表达式如式（2）所示。

式中，Csl为大颗粒与小颗粒的接触数；Ctotal为总的接触数。q 值越小表明混合效果越差，越大表明混合效果越好。

但这种方法对颗粒统计要求极高，很难在实验分析中实现，因此多数被用于数值模拟中的颗粒混合评价。

1.4 Lacey 指数评价法

该方法也可称为混合指数法，是Lacey[18]在1954年利用统计学方法提出的一种针对颗粒混合度的计算方法。他通过对颗粒混合标准差评价法进行分析，结合颗粒混合实际情况，提出混合指数计算式（3）。

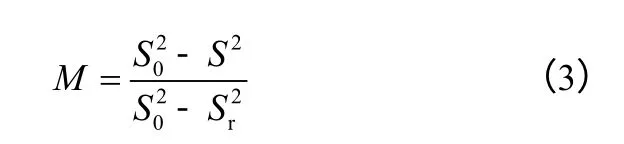
式中，S2为两种颗粒实际混合方差；S02为完全分离时的混合方差；Sr2为两种颗粒完全随机混合方差。各量计算公式如式（4）。

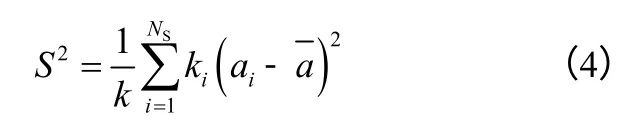
式中，Ns为样本总数；ai为两类颗粒任意一类在样本i 中所占的比例；为相应颗粒在滚筒内所占颗粒比例；ki为样本i 的权重，可表示为式（5）；k 表示为式（6）。

式中，Ni为样本i 内的颗粒数；Nt为颗粒数 总和。

完全分离时的混合方差S02计算公式为式（7）。

式中，P 为一种颗粒所占比例；（1-P）为另一种颗粒所占比例。

两种颗粒完全随机混合方差Sr2计算公式为 式（8）。

式中，n 为每一个样本内平均颗粒数。

该方法与变异系数法有着共同的优点，但在取样上差别比较明显，其取样采用对径向图像网格划分取样法，可利用摄像等设备对实验进行连续取样。

1.5 其它评价法

在混合度研究上国内外学者一直没有停止其前进的脚步，随着对颗粒混合认识的深入，对颗粒混合的算法也在逐渐发展着。Finnie 等[19]用统计焓来衡量混合度，这种方法注重对某一区域内物料比率的计算。Van Puyvelde[20]研究表明，用接触数和统计焓评价混合度分别适用于不同的领域。采用统计焓这种方法重点衡量某一区域内的总体混合，而接触数则用于发展互相混合的颗粒间的换热模型。

通过上文对比发现，混合程度评价方法较合理且应用较广泛的有变异系数法、接触数法及Lacey指数算法，其在混合度评价上各有优劣，且适用范围不同，其中，Lacey 指数算法比较适合评价径向混合；变异系数比较适合评价轴向混合，也可应用于易取料的工业混合测量；变异系数法主要适用于计算机数值模拟中涉及的混合。因此本文作者应用Lacey 指数算法对颗粒混合进行评价。

2 Lacey 指数算法探讨

为了适应不同粒径颗粒群混合度的计算，国内外学者普遍采用等效颗粒数算法对获得的大小颗粒数进行处理，主要方式就是设一标准颗粒，之后将其它颗粒利用等效关系转换成标准颗粒数，如本文中，以1 mm 直径颗粒为标准颗粒，由于只研究径向即二维颗粒混合，故可以将1 个3 mm 直径颗粒或5 mm 直径颗粒按面积等效法转换成9 个标准颗粒（1 mm 颗粒）或25 个标准颗粒，再利用标准颗粒总数代入式（3）～式（8）中进行计算。

Lacey 指数算法在应用过程中可分为取样、提取数据、计算混合度三部分，其中提取数据与计算混合度对于径向混合度并无太大影响，只要能够保证其准确性即可，但在取样上对于颗粒混合影响比较大。Lacey 指数算法取样如图2 所示，其取样样本多少将直接影响到样本内颗粒分布，进而影响总体混合度。因此一种合适的取样将影响颗粒混合评价正确与否。本文作者以33.3%填充率无倾角3.4 r/min 工况为例，分别采用4×4、6×6、8×8、 10×10 共4 种取样方式，分析不同取样对颗粒混合的影响情况。为了全面地研究取样对颗粒混合度的影响，取混合初始时0～8 s 及混合稳定后的52～60 s 两个阶段进行分析。

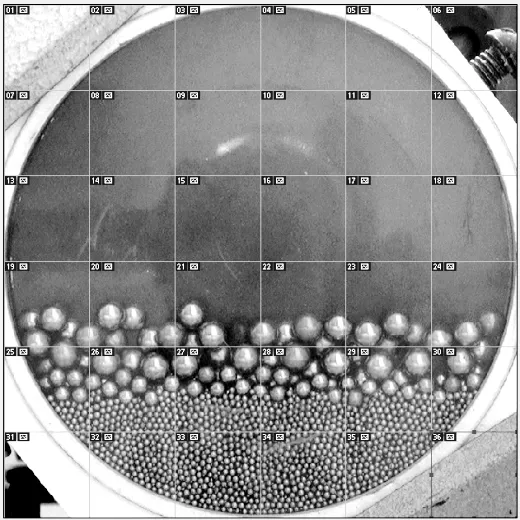
图2 Lacey 指数取样示例

图3 混合初始阶段各取样混合度

2.1 混合数值变化分析

初始0～8 s 各个取样方法混合度如图3 所示，随着样本的增加，混合度逐渐降低，但混合度变化趋于平缓。其中4×4 取样方式下，颗粒混合度的变化最为剧烈，虽然总体变化趋势还是上升的，但上下波动幅度最大；而10×10 取样方式下颗粒混合度变化最为平缓，整体呈现出先略降后缓慢上升的趋势；6×6 取样方式及8×8 取样方式所获得的混合度变化介于4×4 和10×10 两者之间。

为了获得引起这一变化的原因，将取样原图及Lacey 指数算法与混合度曲线进行对比分析。

首先按Lacey 指数算法分析。Lacey 指数计算混合度M 直接涉及的量有S2、S02、Sr2三个，因此针对这3 个量进行分析：其中，根据式（7）可以得出S02只与大小颗粒总数有关，与取样方式无关；Sr2可看作S02/n，其中n值为颗粒总数除以样本个数，在本文中n 值均较大，求出的Sr2均为10-3数量级，与S02（10-1数量级）相差很大，对M 值影响极小，故假设引起图3 现象与Sr2无直接关系；根据式（8）得出S2与单个样本内颗粒总是有直接关系，因此假设S2是引起图3 现象的主要原因。

为了验证上述两点假设，对实验数据作以下分析：用颗粒总数代替n，这样n 将不再受取样方式影响，计算发现其规律与图3 所示规律一致且数据基本无变化，这表明假设一正确；如图4 所示，对比 4×4 取样与8×8 取样0 s 时部分图片，发现其取样空间相同，切割外框线相同，仅是将4×4 中每一样本再次分成4 个样本，但其整体混合度值相差很大，其4×4 时M 值为0.299，而8×8 时M 值为0.1496，这表明样本内颗粒数是引起混合度变化的关键。由于Sr2假设成立，所以S2假设也是成立的。

图4 4×4 取样与8×8 取样对比

在S2计算公式中，k 在本文计算中为恒定值1，为小颗粒在滚筒内所占颗粒比例，即q，并不会因样本取法不同而改变，故这两个量不予分析。因此引起S2变化的只可能与ki、ai有关。

ki与ai在计算过程中都需要样本内等效颗粒数及样本内大小颗粒数，通过图4 能够看出，4×4 取样与8×8 取样其每一样本内颗粒数均有极大变化，特别是8×8 中47、54 与55 三个样本内部包含了1 mm、 3 mm、5 mm 颗粒，这将直接影响ki与ai两个值，从而影响到S2，这也是不同取样所得混合度不同的根本原因，即单一样本内大小颗粒数比例及个数改变引起混合度数值的改变。

为了证明同一样本内颗粒分布是影响混合度数值变化的根本原因，本文对2 s 时刻图像进行如下处理：在3.4 r/min 转速下2 s 时间内可使滚筒旋转40.8°，但这一角度并未引起颗粒间相对位置较大改变，所以2 s 时刻与0 s 时刻混合度理论值应该基本相同，因此将2 s 时刻图像顺时针（滚筒为逆时针旋转）旋转40.8°，获得图像与2 s 时刻初始位置及0 s 时刻图像对比如图5 所示，图5(b)与图5(c)颗粒分布基本无变化，按4×4 取样计算图5(b)混合度为0.3026，这与图5(c)即0 s 时刻混合度0.2992基本相同，但与图5(a)混合度0.4878 相差甚远。

对比其4×4 取样图（图6）发现，在大小颗粒交汇位置样本内颗粒数有很大不同，图6(a)中这一交汇位置单一样本内大小颗粒数相差不多，而图6(b)与图6(c)这一位置单一样本内大小颗粒数相差极大，这就导致这一区域单一样本内混合度前者要远远优于后者，从而引起整体混合度之间的巨大 差异。

图5 滚筒旋转对比图

图6 滚筒旋转取样对比图

通过上述讨论可得，Lacey 指数计算中取样方式对颗粒混合度数值影响主要体现在单一样本内颗粒分布上，单一样本内颗粒个数相差越小，则整体混合值越高。

取上述工况混合稳定阶段52～60 s 图像进行计算得混合度如图7 所示。随着取样数量的增加，其混合度值降低，但其总体趋势变化不大。表明取样不同对混合趋势基本没有影响，但对混合度数值影响较大，这与初始阶段所呈现的规律相同。这表明上述分析结论适用于混合各个阶段。

2.2 取样标准分析

从上文分析结果可以看出，虽然取样方式对颗粒混合曲线趋势影响较小，但对混合度数值影响极大。通过相关性计算得：取样网格大小与颗粒混合度表现为显著性正相关，其相关系数为0.9。因此如何选取取样方式将影响实验数据处理的准确性。

通过图6 及相关结论可以得出，取样空间过大并不利于颗粒混合度的准确分析，由于取样空间过大，其内部易产生大小颗粒群间混合，被误认为颗粒间混合进行计算，这使得计算结果产生较大误差。

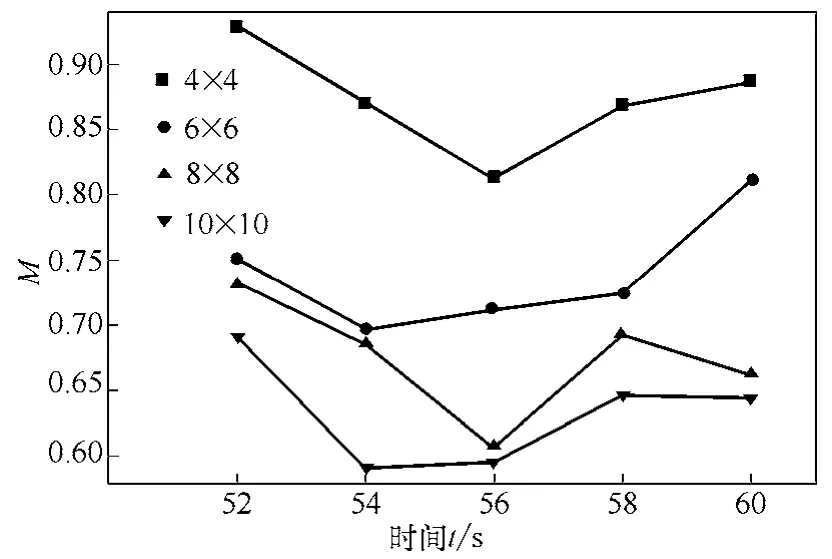
图7 混合稳定阶段各取样混合度

图8 取样引起混合变低示意图

但取样空间过小时，会产生大小颗粒被人为的分离现象，如图8 暗色标记颗粒附近，其上部大颗粒与小颗粒完全混合在一起，但由于网格过小无法将大颗粒附近的全部信息包含在一起，使得其混合度被人为的降低。针对本实验工况计算得：所用颗粒为1 mm、3 mm、5 mm，其大小颗粒理想化均匀横向混合为1 mm 颗粒、3 mm 颗粒，1 mm 颗粒、5 mm 颗粒、1 mm 颗粒分布模式，其横向尺寸为11 mm，则单一样本横向尺寸最好在11 mm 左右，即可将其信息全部包含在内。本研究所取样本4×4、6×6、8×8、10×10 计算成单一样本单边尺寸分别为21 mm、14 mm、10.5 mm 及8.4 mm，则14 mm样本与10.5 mm 样本接近最佳样本，但10.5 mm 样本容易引起图8 所示问题，故14 mm 取样方式即 6×6 取样方式为最佳。通过对比图3 与图7 发现，相对于其它两种取样方式而言，这两种取样方式各项数据变化趋势与其它相同而数值居于中间位置，初始阶段两种取样方式下混合度变化基本相同，但稳定阶段8×8 取样方式下颗粒混合度上下变化较大，相对而言6×6 取样方式优于8×8 取样方式。其结果验证了理想混合度计算选取的取样方式的正确性。

为了进一步验证此结论对三组元颗粒径向混合评价上的广泛性，对6.8 r/min、10 r/min 及16.7%填充率3.4 r/min 工况稳定阶段进行计算得如图9 所示结果。结果表明，不同取样方式所引起的混合度变化基本相同。这一结果表明上述取样方式普遍适用于三组元颗粒混合实验。

3 结 论

对比分析多种混合度评价方法，较常用的混合度评价方法为变异系数、接触数及Lacey 指数，其中变异系数比较适合评价轴向混合，也可应用于易取料的工业混合测量；接触数法主要适用于计算机数值模拟中涉及的混合；Lacey 指数算法比较适合评价径向混合。

图9 混合度综合取样

通过对Lacey 指数算法取样方式对比分析可知，在同一工况下不同取样方式所得混合度有很大差异，其原因在于不同取样方式引起单一样本内大小颗粒比例不同，从而引起S2值产生较大变化，最终引起M 值变化；在实验处理上最佳取样尺寸应该略大于颗粒最佳混合时横向尺寸；本实验所得最 佳取样尺寸为单一样本单边长14 mm，即6×6 取样方式。

[1] 卢寿慈. 粉体技术手册[M]. 北京：化学工业出版社，2004：590-603.

[2] Williams J C. The segregation of Powders and granular materials[J]. Fuel Soeiety Journal，1963，14：29-35.

[3] Hogg R，Cahn D S，Healy T W，et al. Diffusional mixing in an deal system[J]. Chemical Engineering Science，1966，21（11）：1025-1038.

[4] Li Shuiqing，Yao Qiang，Chen Bing，et al. Molecular dynamics simulation and continuum modeling of granular surface flow in rotating drums[J]. Chinese Science Bulletin，2007，52（5）：692-700.

[5] 李水清，姚强，陈冰，等. 回转筒颗粒表面流的分子动力学模拟和连续理论[J]. 科学通报，2006，51（19）：2319-2326.

[6] Ottino J M，Khakhar D V. Mixing and segregation of granular materials[J]. Annual Review of Fluid Mechanics，2000，32：55-91.

[7] Ottino J M，Lueptow R M. On mixing and demixing[J]. Science，2008，319（5865）：912-913.

[8] Pérez-Alonso C，Delgadillo J A. Experimental validation of 2D DEM code by digital image analysis in tumbling mills[J]. Minerals Engineering，2012，25（1）：20-27.

[9] Jha A K，Puri V M. Percolation segregation of multi-size and multi-component particulate materials[J]. Powder Technology，2010，197（3）：274-282.

[10] Cleary P W，Metcalfe G，Liffman K. How well do discrete element granular flow models capture the essentials of mixing processes?[J]. Applied Mathematical Modelling，1998，22（12）：995-1008.

[11] Siiriä S，Yliruusi J. DEM simulation of influence of parameters on energy and degree of mixing[J]. Particuology，2011，9（4）：406-413.

[12] 赵永志，程易. 水平滚筒内二元颗粒体系径向分离模式的数值模拟研究[J]. 物理学报，2008，57（1）：321-328.

[13] 赵永志，张宪旗，刘延雷，等. 滚筒内非等粒径二元颗粒体系增混机理研究[J]. 物理学报，2009，58（12）：8386-8393.

[14] Jiang Maoqiang，Zhao Yongzhi，Liu Gesi，et al. Enhancing mixing of particles by baffles in a rotating drum mixer[J]. Particuology，2011，9（3）：270-278.

[15] 张立栋，李少华，余侃胜，等. 油页岩与固体热载体在回转干馏炉内混合特性的冷态实验[J]. 化工进展，2011，30（3）：492-497.

[16] Van Puyvelde D R，Young B R，Wilson M A，et al. Experimental determination of transverse mixing kinetics in a rolling drum by image analysis[J]. Powder Technology，1999，106（3）：183-191.

[17] 李少华，张立栋，张轩，等. 回转干馏炉内影响颗粒混合运动因素的数值分析[J]. 中国电机工程学报，2011，31（2）：32-38.

[18] Lacey B P M C. Developments in the theory of particle mixing[J]. Journal of Applied Chemistry，1954，4：257-268.

[19] Schutyser M A I，Padding J T，Weber F J，et al. Discrete particle simulations predicting mixing behavior of solid substrate particles in a rotating drum fermenter[J]. Biotechnology and Bioengineering，2001，75（6）：666-675.

[20] Van Puyvelde D R. Comparison of discrete elemental modeling to experimental data regarding mixing of solids in the transverse direction of a rotating kiln[J]. Chemical Engineering Science，2006，61（13）：4462-4465.