基于邻域粗糙集和距离判别的信用风险评级

郭春花

(重庆大学数学与统计学院，重庆 401331)

信用风险评级是金融管理领域的热门话题。一些传统和非传统的方法如多元统计分析、人工神经网络［1］、支持向量机［2－6］、数据挖掘［7］等已被广泛应用到该领域，并取得了大量的研究成果。随着技术的进一步发展，一些综合的方法［8－9］也被广泛应用于信用风险评级中。我国的信用分析和评估技术仍处于传统的比率分析阶段，信用风险的分析仍然是以单一投资项目、贷款和证券为主，对衍生工具、表外资产的信用风险以及信用集中风险的评估尚属空白。信用数据多具有高维性特点，且既有数值型属性也有类别型属性，与单一的数值型属性相比，在处理上更为复杂。邻域粗糙集方法与其他降维方法相比是一种软计算方法，无需提供样本数据之外的任何先验知识或附加信息，对不确定性的描述有具体的数学公式，减少了算法的随意性，近年来在数据降维［10－11］和分类问题［9，12］中得到了广泛应用。同时信用数据的数值型属性在量纲上的差异较大，所以在信用评级中考虑量纲的差异具有重要意义。基于上述问题，本文提出了一种基于邻域粗糙集和距离判别的信用风险评级方法。用邻域粗糙集对训练样本数据作降维处理，去掉冗余的数据，简化计算过程。距离判别中采用马氏距离消除了数据在量纲上的差异对分类的影响。最后通过实验对该方法的有效性进行了验证。

1 基于邻域粗糙集特征选择的距离判别

1.1 特征选择的邻域粗糙集方法

设分类样本含有p个变量，它们构成p维随机向量X=(X1，X2…Xp)T。为了避免遗漏重要信息，往往要考虑尽可能多的与分类有关的属性，此时会产生2个问题:①随着属性个数p增大，计算量显著增加，问题分析的复杂性明显提高;②各属性之间存在着一定的相关性，使得观测样本反映的信息在一定程度上有重叠。

为了解决上述2个问题，本文采用邻域粗糙集方法对样本变量进行选择。

粗糙集［13－14］理论最早是由Pawlak提出来的，它可以挖掘属性之间的相关性，选择相关属性，去掉无关属性，实现数据降维。本文的邻域粗糙集特征选择对属性集中的数值型属性和类别型属性分别作了讨论。对类别型属性考虑的是它们的等价关系，对数值型属性考虑的是它们的邻域关系。邻域定义如下:∀xi∈U，xi的邻域关系为

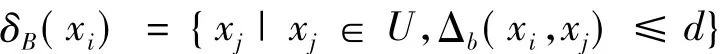
Δ 是 距 离 函 数， 通 常 Δp(xi，xj)=上、下近似分别定义为:

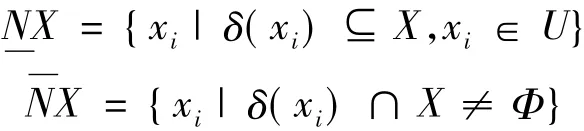
邻域粗糙集属性选择采取前向贪心搜索策略，通过测试加入新的候选属性后度量指标的变化来生成新的属性集，以粗糙集属性依赖度作为度量指标。属性依赖度的具体描述如下:

设a∈A －BSIG(a，B，D)=γB∪a(D)－ γB(D)=POSR(B∪a)－POSR(B)，其中R是U上的等价关系，POSR(B∪a)和POSR(B)分别表示B∪a，B的正域。SIG(a，B，D)反映了属性 a的增加对信息量的影响，显然 SIG(a，B，D)∈［0，1］。如果 SIG(a，B，D)=0，说明属性a的增加没有增加任何的信息，因此a是完全多余的，可以将其删除，从而降低特征的维数，减少计算量。

邻域粗糙集特征选择的具体步骤:

根据给定的信用数据集合，构造并输入决策表(U，Ac∪An∪D)以及 β、d，其中:Ac、An分别代表类别型属性集和数字型属性集;β是一个计算变量精度近似的阈值;d是邻域半径，记输出结果为Red。然后按如下步骤进行:

第1步 ∀a∈Ac计算等价关系Ra，∀a∈An，计算邻域关系Na。

第2步 令Red=φ，其中Red为已选择的特征构成的集合。∀ai∈A － Red，计算 γRed∪a(D)=γRed(D)，这里定义

第3步 选择满足 SIG(ak，Red，D)=SIG(ai，Red，D))的特征 ak。

第4步 如果 SIG(ak，Red，D)＞ε(其中 ε 是用来控制收敛性的一个正数)，则令Red=Red∪ak，回到第2步，直到所有的ai∈A－Red都被进行上述选择为止。

第5步 给出最终被选择特征的集合Red。

设M={x1，x2…xn}是某一个类S的训练集，训练集中的每个样本包括p个属性X1，X2…Xp，经过邻域粗糙集方法进行特征选择后p个属性变为m个属性，分别记为X'1，X'2…X'm。用经过邻域粗糙集特征选择后的样本集合代替原始样本进行下面的距离判别。

1.2 两分类问题的距离判别

传统的距离判别使用的距离多为欧氏距离［15－16］，但欧氏距离中每个坐标对其的贡献是同等的，当坐标轴表示测量值时，往往带有大小不等的随机波动，合理的方法是对坐标加权。同时，欧氏距离的另一个缺点就是当个分量为不同性质的量时，“距离”的大小往往与指标的单位有关系。基于上述缺点，本文为了消除各指标量纲之间的差别对分类的影响，采用马氏距离作为分类依据。

设x'1，x'2…x'n的均值向量为μ，协方差矩阵为∑。给定待判样本x，记dm(x，S)为x与类S之间的马氏距离，并以此距离来度量x与类S之间的相似性，为了方便直接计算d2(x，S)，

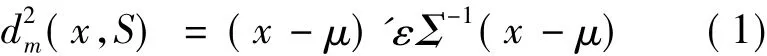
对于两分类问题，设S1、S2是2个类，分别从2类中选择n个样本，每个样本有p个指标，记为S1={x1，x2…xn}。用邻域粗糙集进行特征选择后上述训练集变为 M1={x'1，x'2…x'm}，M2={y'1，y'2…y'l}(m，l＜n)。设 M1、M2的均值向量分别为μ1、μ2，协方差矩阵分别为 Σ1、Σ2，待测样本 x 与 S1、S2之间的马氏距离分别记为 dm(x，S1)和dm(x，S2)。分以下情况讨论:

1) 当 Σ1= Σ2= Σ 时，考 察)与(x，S2)的差，则有

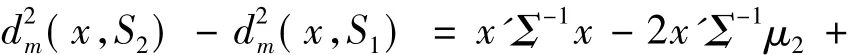
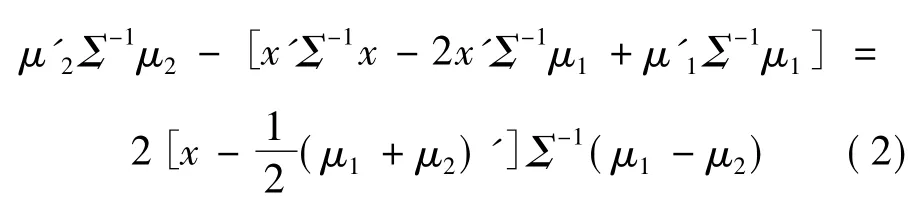
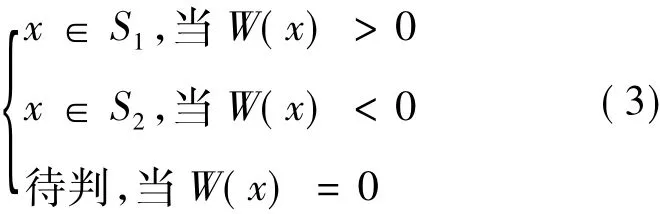
2) 当 Σ1≠Σ2时，可用

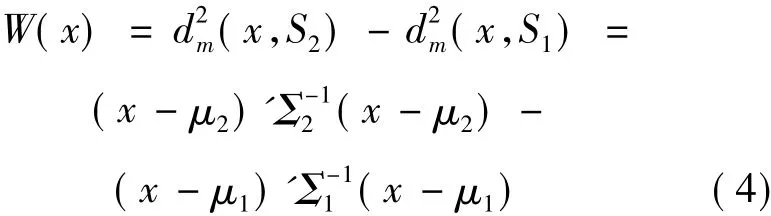
进行判别，判别准则同式(3)。

实际中参数μ1、μ2和Σ都是未知的，通常通过样本数据取其无偏估计。将上述估计值代入式(2)、(4)计算即可。

基于邻域粗糙集的距离判别算法的步骤如下:

1)对于每类的训练集样本，用邻域粗糙集的方法进行特征选择，具体做法如本文1.1节所述。

2)将每类的训练集样本数据用选出的特征表示，计算出各类训练集的均值向量和方差。

3)对于给定的待判样本x，根据式(2)或(4)计算x与各类训练集的马氏距离之差。

4)根据式(3)判断x的归属。

2 实验分析

信用风险评级是借贷机构根据客户提供的信息，构造某种分类器对其进行分类，以便做出正确的借贷决策，确保损失达到最小的过程。对一组德国的信用数据［15］用本文的方法进行分类实验。该数据包括1 000个样本，其中700个样本属于“信用好”型，另外的300个样本属于“信用差”型。每个样本含有包括借贷目的、借贷金额、工作性质，以及个人信息在内的24项衡量指标。为了说明该法的分类有效性，同时对此数据用 Linear SVM，RBF-kernel SVM等方法进行分类，并将结果进行比较。实验结果包括2类各自的分类准确率和总体分类准确率。为了方便设定为“信用好”型和“信用差”型，总体的分类准确率分别记为a1、a2、a，测试集中被正确分为“信用好”“信用差”，被正确分类的样本书分别记为b1、b2、b，测试集为“信用好”“信用差”，测试集总的样本数分别记为c1、c2、c，则:

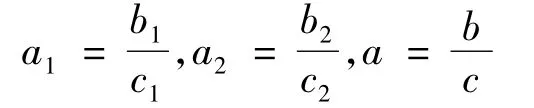
将24项衡量指标分别记为 x1，x2…x24，经过邻域粗糙集特征选择后被选出的特征为x1，x2，x3，x4，x6，x7，x8，x9，x11，x12，x13，x14。实验中每类分别随机选取40、60、80、100、120、140、160、180 个样本作为训练集，剩余样本作为测试集，每种情况重复实验20次，最后取平均值作为该情况下的结果。实验结果如表1～3所示。

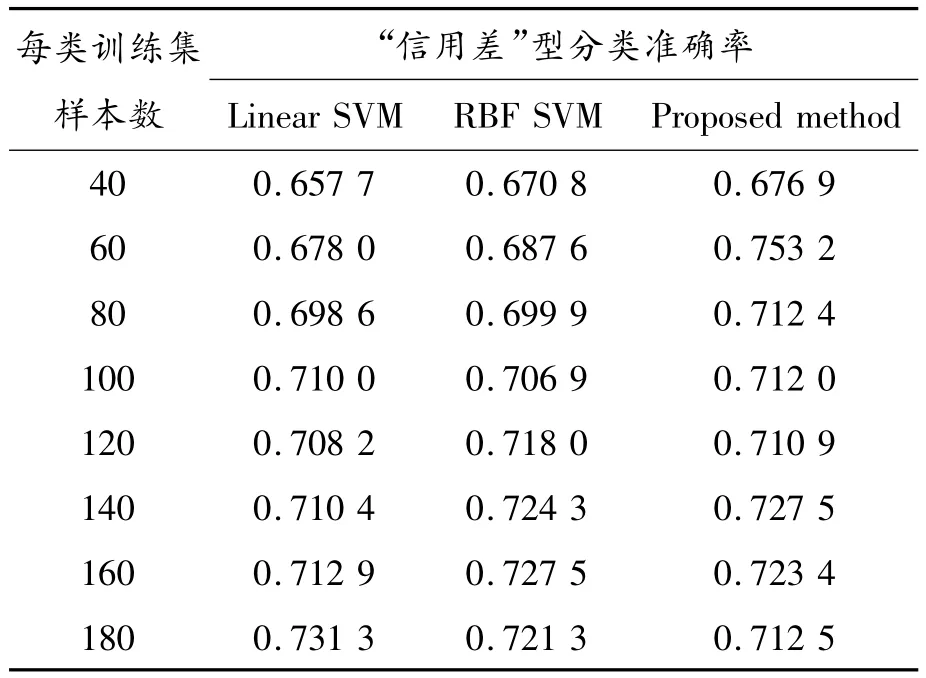
表1 “信用差”型分类准确率比较

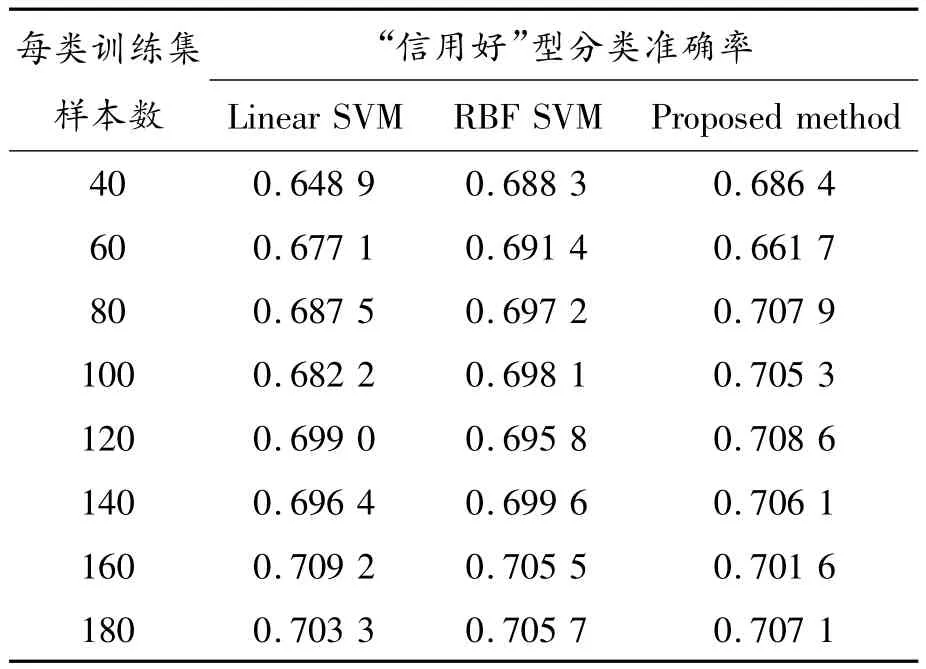
表2 “信用好”型分类准确率比较

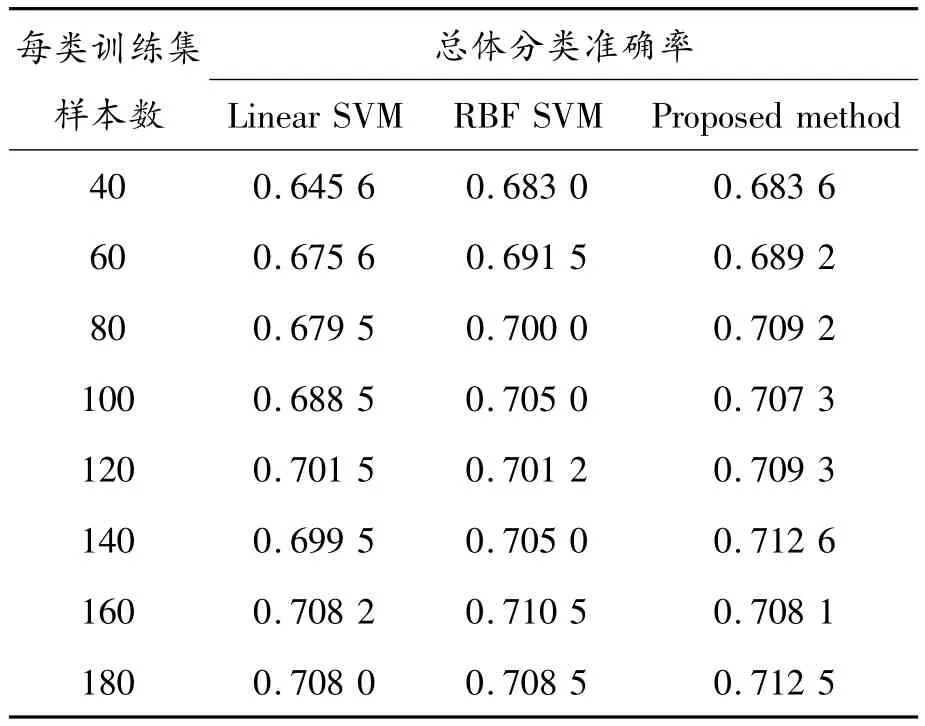
表3 总体分类准确率比较

从表1可以看出当训练集样本数为80、100、120、140、180时，本文提出的方法对“信用差”型样本的分类效果要优于其他2种方法。由于将一个本属于“信用差”的样本误判带来的损失要远远大于将一个本属于“信用好”的样本误判带来的损失，所以提高“信用差”型样本的分类准确率是信用风险评级的一个最为重要的目标。从表1看到:当训练集样本数量大于等于60时该法对“信用差”型样本的分类准确率均超过了70%。这也说明了该方法的有效性。

从表2可以看到当训练集样本为40、60、80、140时本文提出的方法对于“信用好”这类的分类准确率要高于其他2种方法。同时，本文提出的方法对于“信用好”这类的分类准确率大都在70%以上。

从表3可以看到当训练集样本数量为40、80、100、120、140、180时本文提出的分类方法的总体准确率超过了其他2种方法，而当训练集样本数为60、160时RBF SVM方法效果较好。

根据上述实验结果认为，基于邻域粗糙集和距离判别信用风险评级方法是一种更为有效的评级方法。

3 结束语

本文提出了一种基于邻域粗糙集和距离判别的信用风险评级方法。通过邻域粗糙集特征选择去掉了样本中的冗余信息，快速降低了样本属性的维数，简化了计算过程。距离判别中采用马氏距离，消除了各属性量纲差异对分类带来的不良影响。应用该法对现实数据进行实验。结果表明，基于邻域粗糙集和距离判别的信用风险评级方法是一种更为有效的分类方法。

［1］Angelini E，Tollo G，Roli A.A neural network approach for credit risk evaluation［J］.The Quarterly Review of E-conomics and Finance，2008，48(4):733 －755.

［2］Bellotti T，Crook J.Support Vector machines for credit scoring and significant features.［J］.Expert systems with Applications，2009，36(2):3302 －3308.

［3］Danenas P，Garsva G，Saulius Gudas.Credit Risk Evaluation Model Development Using Support Vector Based Classifiers［J］.Procedia Computer Science，2011(4):1699－1707.

［4］余珺，郑先斌，张小海.基于多核优选的装备费用支持向量机预测法［J］.四川兵工学报，2011(6):118－119.

［5］万辉.一种基于最小二乘支持向量机的图像增强算法［J］.重庆理工大学学报:自然科学版，2011(6):53－57.

［6］邬啸，魏延，吴瑕.基于混合核函数的支持向量机［J］.重庆理工大学学报:自然科学版，2011(10):66－70.

［7］Bee Wah Yap，Seng Huat.Nor Huselina Mohamed Husain Mohamed Husain.Using data mining to improve assessment of credit worthiness via credit scoring models［J］.Expert Systems withApplication，2011，38(10):13274－13283.

［8］Lean Y，Yao X，Wang S Y.Credit risk evaluation using a weighted least squares SVM classifier with design of experiment for parameter selection［J］.Expert systems with Application，2011，38(12):15392 －15399.

［9］Yao P，Lu Y H.Neighborhood rough set and SVM based hybrid credit scoring classifier［J］.Expert systems with Application，2011，38(9):11300 －11304.

［10］Hu Q H，Daren Yu，Liu J F.Neighborhood rough set based heterogeneous feature subset selection［J］.Information Sciences，2008，178:3577 －3594.

［11］Meng Z Q，Shi Z Z.Extended rough set-based attribute reduction in inconsistent incomplete decision systems.［J］.Information Sciences，2012，204:44 －69.

［12］Zhang S W，Huan D S，Wang S L.A method of tumor classification based on wavelet packet transforms and neighborhood rough set［J］.Computers in Biology and Medicine，2010，40:430 －437.

［13］Pawlak Z.Rough sets［J］.International Journal of Computer and Information Science，1982，11:341 －356.

［14］王磊，王金山，沈浮.一种基于灰色绝对关联度的变精度粗糙集模型［J］.重庆理工大学学报:自然科学版，2012(5):123－126.

［15］Zhou X F，Jiang W H，Shi Y.Credit risk evaluation by using nearest subspace method［J］.Procedia Computer Science，2010(1):2449 －2455.

［16］Zhou X F，Jiang W H，Shi Y.Credit risk evaluation with kernel-based affine subspace nearest points learning method［J］.Expert systems with Application，2011，38(4):4272－4279.