同轴对转行星齿轮传动系统的固有特性

刘 敬，石万凯，邹卓航

(1.重庆大学机械传动国家重点实验室，重庆 400044;2.武汉理工大学信息工程学院，武汉 430070)

行星齿轮传动系统具有体积小、传动比大、承载能力强等优点。同轴对转传动系统不仅具有普通行星齿轮传动的特点，还可以将单一输入转换成两个输出，实现减速增扭的作用。

国内外学者对行星齿轮系统的固有特性进行了深入研究［1－11］。Kahraman 等［1－2］采用集中质量法建立了行星齿轮系统的非线性时变动态模型，考虑不同误差种类对系统动态特性的影响，并通过实验模型验证了不同误差与行星轮个数对系统动态特性的影响。Lin和Parker［3］建立了直齿行星齿轮传动系统的扭转－横向耦合模型，分析了无阻尼振动下系统的3种振动模式:扭转振动、横向振动和行星轮振动。Zhu等［4］建立了柔性销轴行星传动系统的动力学模型，分析了其模态特性与不同变量对固有频率灵敏度的影响。赵永强等［5－6］以人字齿封闭行星轮系为研究对象，指出了系统存在星形轮系振动模态、行星轮系振动模态和耦合振动模态，并对其进行了模态跃迁现象分析。罗玉涛等［7］推导并建立了混合动力传动系统的纯扭转动力学模型，讨论了耦合刚度对系统固有频率的影响。秦大同等［8－9］基于Lagrange方程建立了盾构机多级行星齿轮传动的动力学模型，并分析了该系统的模态特性、位移响应和加速度响应等特性。

1 齿轮传动系统的动力学模型

同轴对转传动系统如图1所示。定轴轮系由太阳轮Zs1、行星轮Zpi(i=1，2，…，N)和内齿圈Zr1组成;差动轮系由太阳轮Zs2、行星轮Zmj(j=1，2，…，M)、内齿圈Zr2和行星架C组成，其中，内齿圈是双齿圈且采用相同的几何参数。输入扭矩通过太阳轮分流传递给定轴轮系机构与差动轮系机构，并通过内齿圈和行星架C分别形成输出A和B。

为了简化计算模型，在建立同轴对转系统的平移－扭转齿轮传动系统的动力学模型时做以下假设:各个构件为刚体;各级行星轮在圆周均匀分布，其平移质量与转动惯量分别相等;系统中各个构件的支撑刚度为常值，各对齿轮之间的啮合刚度也为常值，忽略啮合阻尼对系统的影响;忽略齿轮对啮合时的摩擦力、传递误差等。

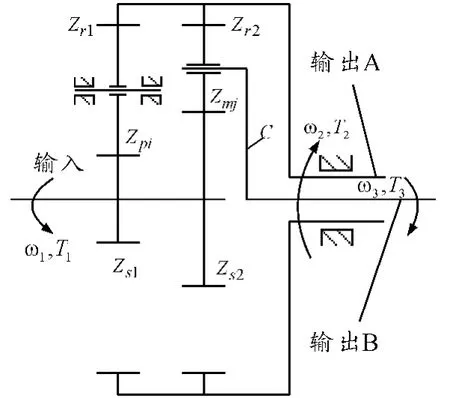
图1 同轴对转传动系统

基于集中质量参数法建立同轴对转传动系统的动力学模型。图2(a)为固定坐标系下定轴轮系的动力学模型，其中Kspi为太阳轮Zs1与行星轮Zpi的啮合刚度，Krpi为内齿圈 Zr1与行星轮 Zpi的啮合刚度;图2(b)为差动轮系以行星架转速ωc为动坐标的动力学模型，其中Ksmj为太阳轮Zs2与行星轮Zr2的啮合刚度，Krmj为内齿圈Zr2与行星轮Zmj的啮合刚度。图(2)中:k1为太阳轮Zs1、Zs2之间的耦合扭转刚度;k2为内齿圈Zr1、Zr2之间的耦合扭转刚度;kC为行星架的扭转刚度;kr1、kr2分别为内齿圈 Zr1、Zr2的支撑刚度;kp1、kp2分别为行星轮 Zpi、Zmj的支撑刚度。行星轮支撑刚度按Montestruc［10］提供的方法进行计算。

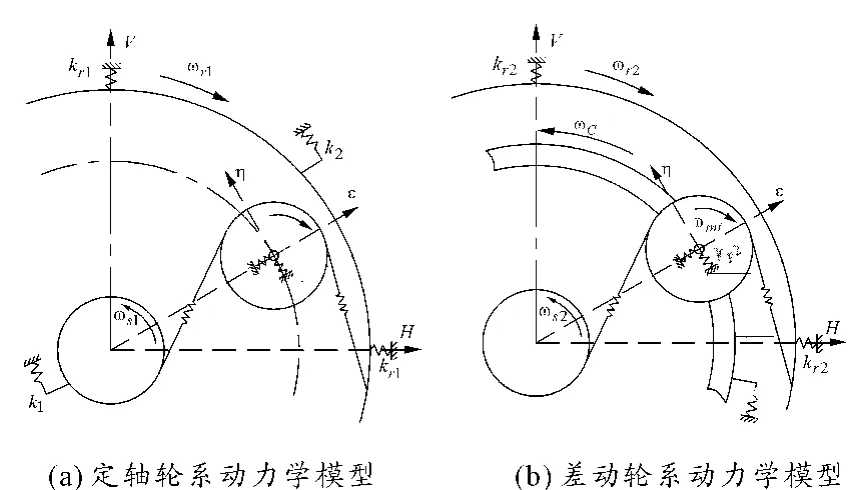
图2 同轴对转系统动力学模型

同轴对转传动系统共有(13+3N+3M)个自由度，其广义坐标如下:

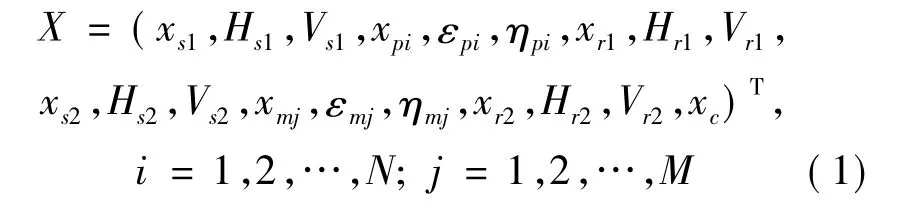
式(1)中:xs1、xpi、xr1、xs2、xmj和 xr2分别为齿轮 Zs1、Zpi、Zr1、Zs2、Zmj和 Zr2沿啮合线的微位移;Hxy和 Vxy(x=s，r;y=1，2)分别为齿轮xy中心的横向和纵向微位移;εpi和ηpi为行星轮Zpi中心的径向和切向微位移，εpi和ηpi为行星轮Zmj在动坐标系下中心的径向和切向微位移;xC为行星架C在其半径rC上的切向微位移。

2 同轴对转系统的动力学平衡方程

设δspi和δrpi为定轴轮系第i个行星轮与太阳轮和内齿圈沿啮合线的等效微位移，δsmj和δrmj为差动轮系第j个行星轮与太阳轮和内齿圈沿啮合线的等效微位移，则:

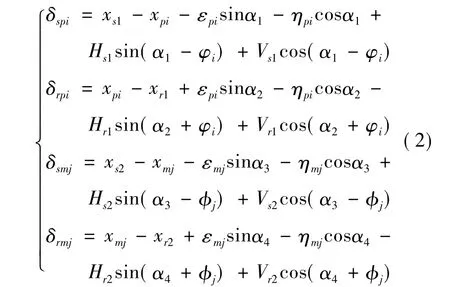
式(2)中:φi=2π(i－1)/N 为定轴轮系第 i个行星轮相对于第1个行星轮的位置角;φi=2π(j－1)/M为差动轮系第j个行星轮相对于第1个行星轮的位置角;α1和α2分别为定轴轮系行星轮与太阳轮和内齿圈的啮合角，α3和α4分别为差动轮系行星轮与太阳轮和内齿圈的啮合角。

根据Lagrange方程推导出同轴对转系统各个自由度的振动微分方程。

定轴轮系平衡方程:

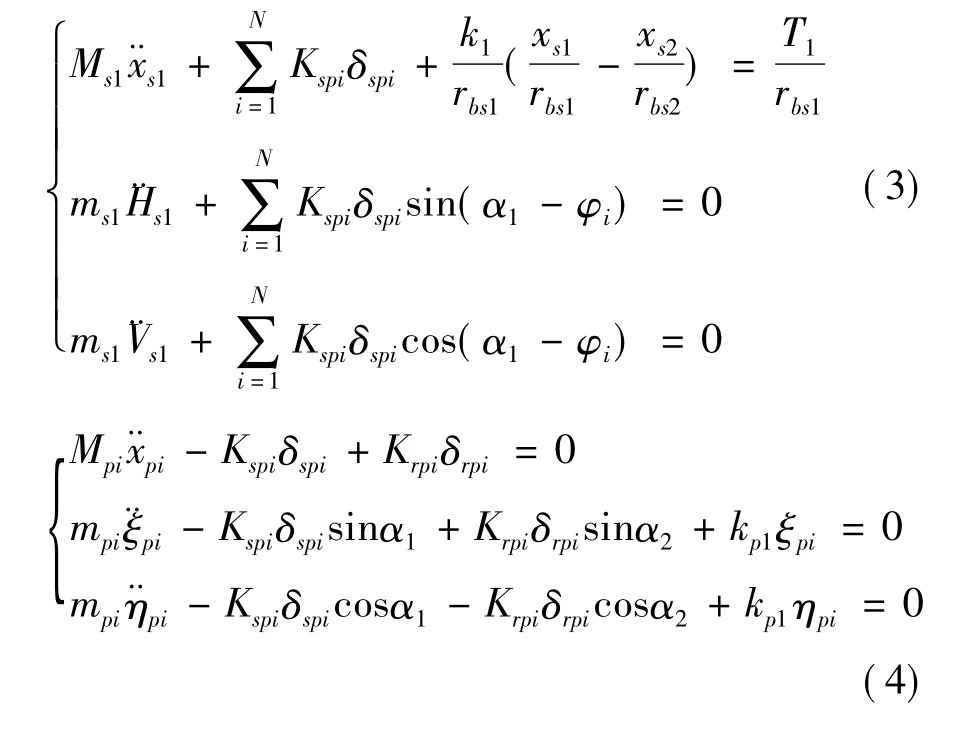
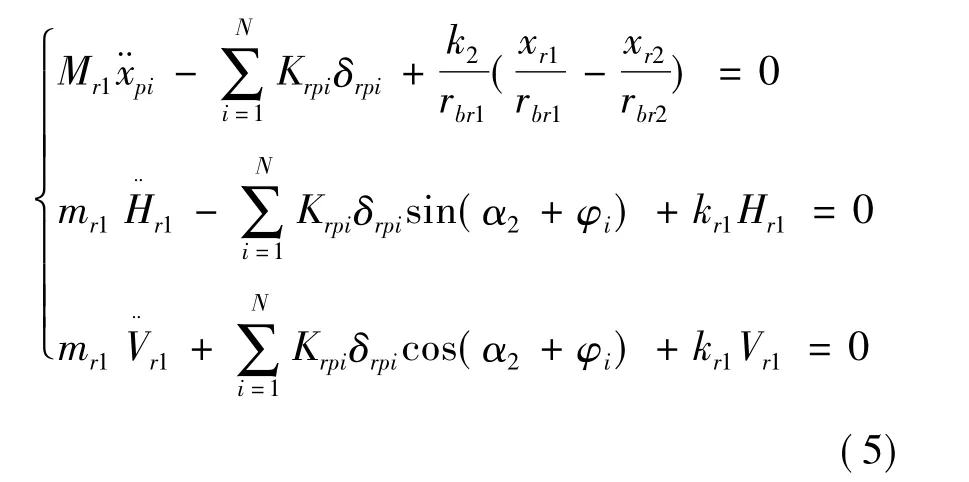
差动轮系平衡方程:

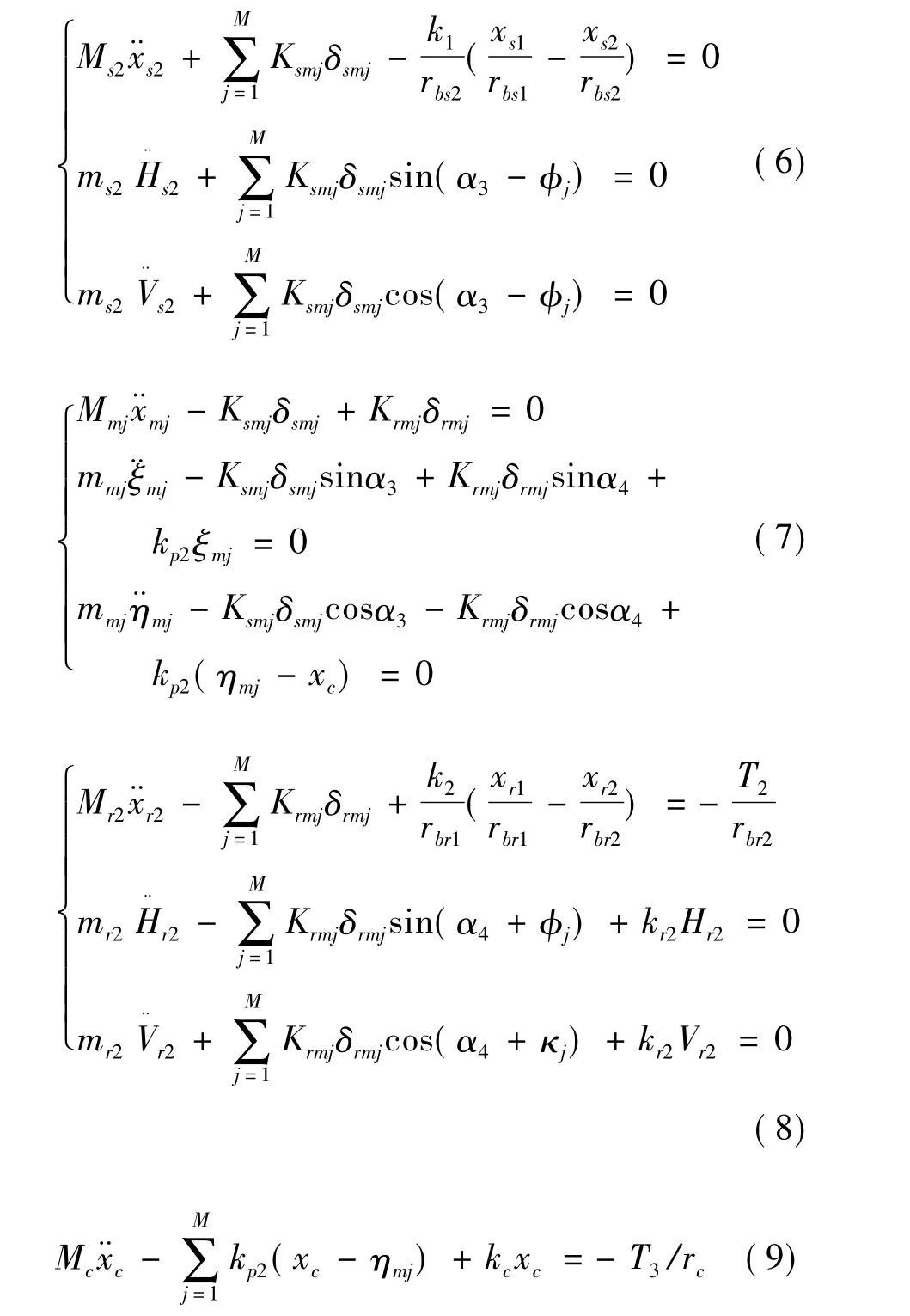
其中:M和m分别为各个构件的等效质量和平移质量，且M=J/r2;J为构件的转动惯量，对于齿轮，r是其基圆半径rb，对于行星架，r是其当量基圆半径rbc;T1为同轴对转系统的输入扭矩，T2为差动轮系内齿圈Zr2的输出扭矩，T3为差动轮系行星架C的输出扭矩。

将方程(3)～(9)整理成如下的矩阵形式:

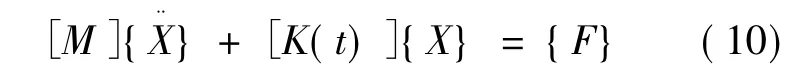
其中:M、X分别为广义质量矩阵和广义坐标位移列阵;F为外载荷列阵;K为刚度矩阵。

3 固有特性分析

根据式(10)建立的同轴对转系统平移－耦合动力学模型对系统进行模态分析，可得到系统的各阶固有频率与对应的振型。式(10)对应的特征值问题为

其中:ωi为系统的第i阶固有频率;φi为对应固有频率下的振型矢。

表1给出了某一同轴对转系统的几何参数，通过计算可以得到系统的各阶固有频率与振型矢量。主要考虑系统不同的振动模式、两级行星轮个数与固有频率重根数的关系、行星轮个数的改变对振动模式的影响、系统耦合刚度的变化对固有频率的影响等。

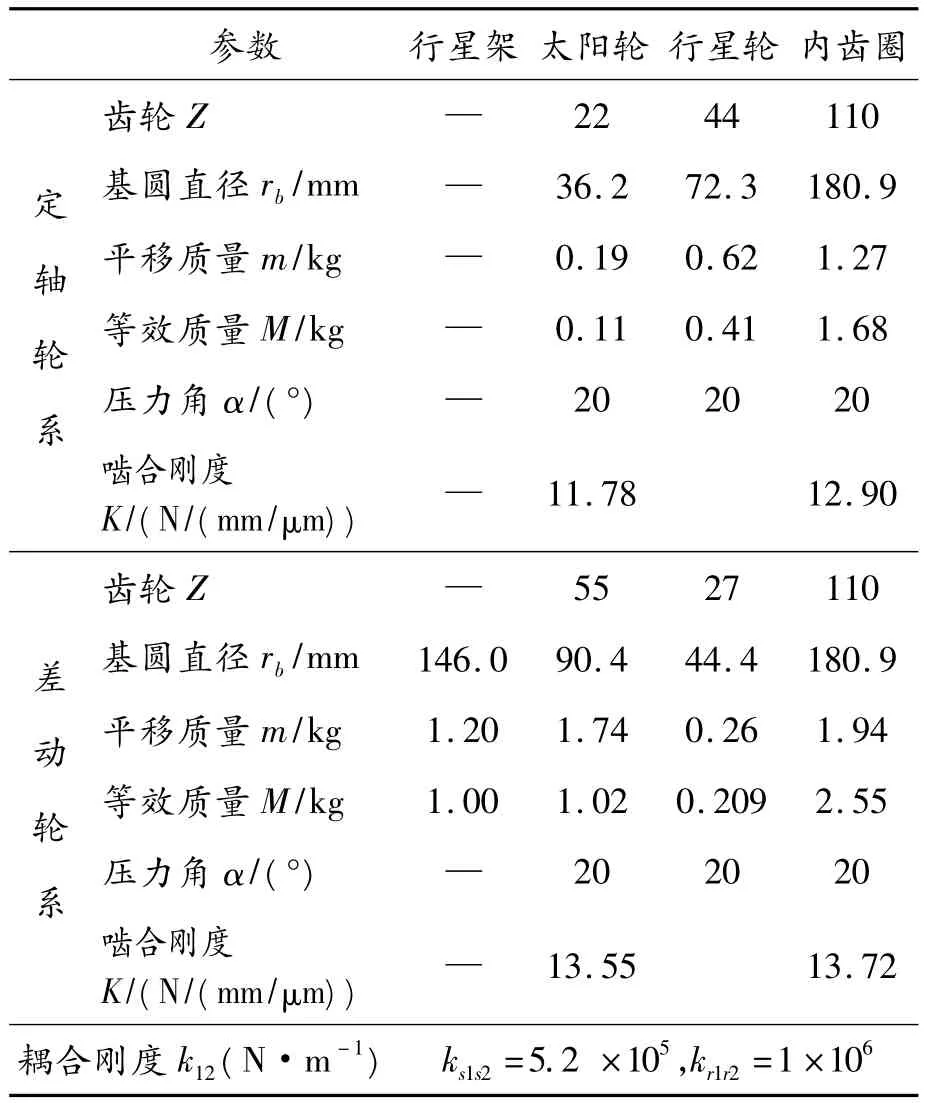
表1 同轴对转系统的几何参数

表2列出了定轴系统行星轮N=3时，系统在差动轮系行星轮M=3、4、5下的固有频率，同时分析了不同固有频率下系统的振动矢量，得到以下的结论:

1)定轴轮系振动模式

①此时差动轮系振动幅值为0，定轴轮系各构件主要表现为平移模式振动，即中心构件的扭转振动为0。图3为定轴轮系振动模式的振型图。

②随着差动轮系行星轮个数的增加，定轴轮系各振动频率不发生变化，差动轮系振动频率个数为(3M+1)。

2)差动轮系振动模式

①此时定轴轮系各构件振动幅值为0。当M为奇数时，差动轮系的振动频率均为重根，重根数为(3M+1)/2，各构件主要表现为平移模式振动;当M为偶数时，差动轮系的振动频率有单根和重根，此时单根主要表现为差动级行星轮模式振动，重根主要表现为平移模式振动。图4为差动轮系振动模式的振型图。

②定轴轮系行星轮一定时，随着差动轮系行星轮个数的增加，系统的振动频率变化趋势为逐渐增大，这与文献［5］中的结果一致。

表2 定轴系统行星轮的固有频率(N=3)

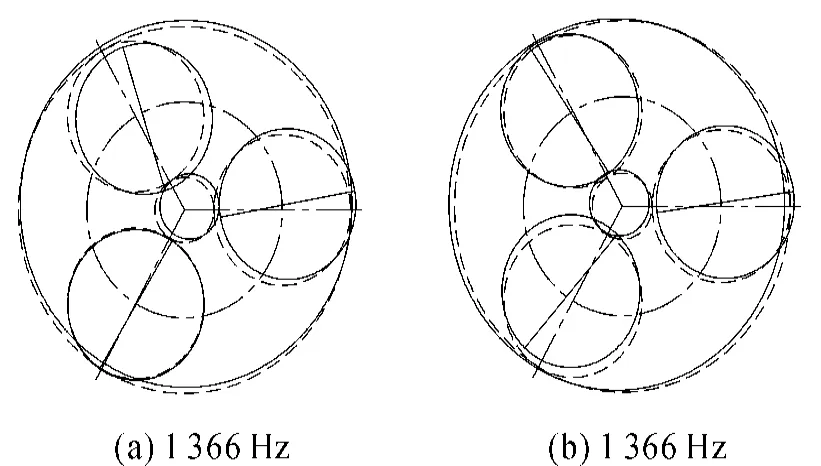
图3 定轴轮系振动模式振型图(M=3，N=3)

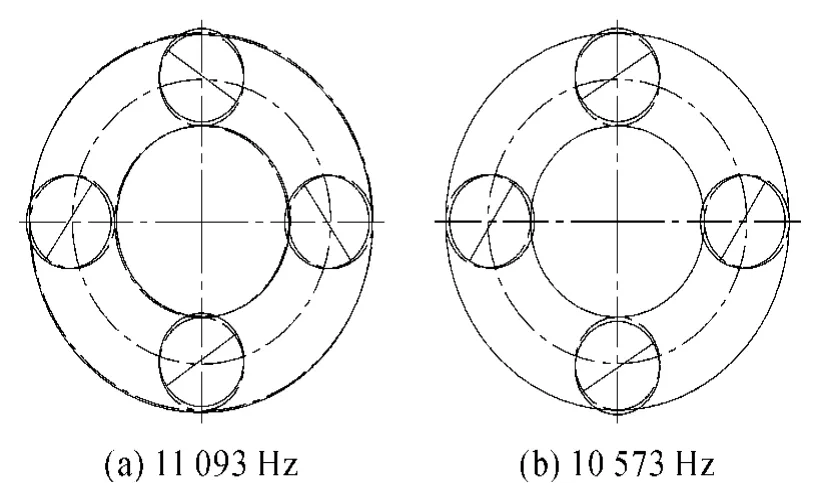
图4 差动轮系振动模式振型图(M=4，N=3)

3)耦合振动模式

①随着差动轮系行星轮个数的增加，耦合振动频率个数不发生变化，共有11个固有频率，并且无重根。

②系统的振型主要为两级构件的扭转模式振动。图5为耦合振动模式的振型图。

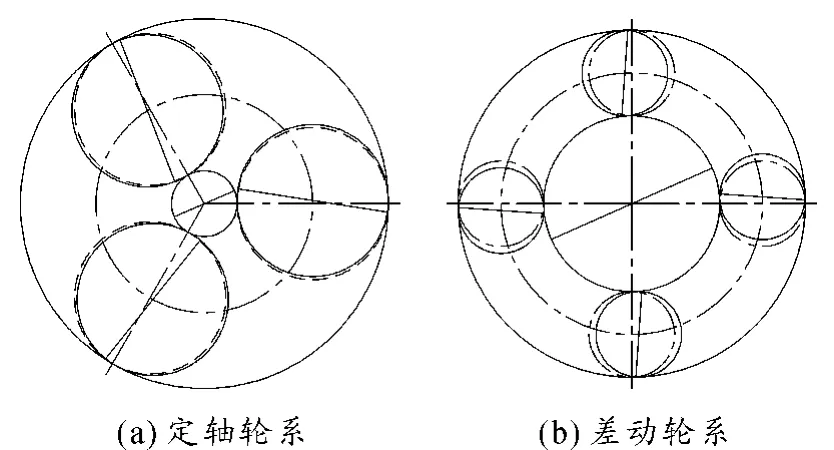
图5 耦合振动模式振型图(M=4，N=3，f=230 Hz)

4 系统的耦合刚度对固有特性的影响

定轴轮系与差动轮系有两种不同的耦合，即两个太阳轮的扭转耦合与两个内齿圈的扭转耦合。以两太阳轮的耦合刚度为设计变量，两内齿圈的耦合刚度为定值，考查不同太阳轮扭转耦合刚度下系统的固有频率变化情况。此时取两级行星轮个数为 M=N=3，k2=1.0 ×106，计算不同太阳轮耦合刚度下系统的固有频率，可以得到如下结论:扭转刚度的变化对定轴轮系振动模式和差动轮系振动模式的固有频率没有影响，各阶频率保持不变。说明定轴轮系振动模式和差动轮系振动模式的固有频率只与齿轮的啮合刚度和质量有关，与扭转耦合刚度无关，与文献［7］的结论一致。表3列出了太阳轮耦合扭转刚度下系统的固有频率。随着两太阳轮耦合刚度的增加，耦合振动模式的固有频率也相应递增。

表3 太阳轮耦合扭转刚度下系统的固有频率(M=3，N=3)

5 结论

1)基于Lagrange方程采用集中参数法建立了同轴对转传动系统的平移－扭转耦合动力学方程，分析了其固有特性。

2)同轴对转系统具有3种不同的振动模式:定轴轮系振动模式、差动轮系振动模式和耦合振动模式。讨论了不同差动轮系行星轮个数对系统固有特性的影响，指出了重根数与行星轮个数的关系，与前人的相关研究结论吻合。

3)通过计算不同太阳轮扭转耦合刚度下系统的固有频率，说明定轴轮系振动模式和差动轮系振动模式下的固有频率没有变化，仅影响耦合振动模式的固有频率，并且随着耦合刚度的递增，耦合振动模式的固有频率也相应增大。

［1］Kahraman A.Load sharing characteristics of planetary transmissions［J］.Mechanisms and Machine Theory，1994，29(8):1151 －1165.

［2］Kahraman A.Static load sharing characteristics of transmission planetary gear sets:model and experiment［J］.SAE Transactions，1999，108(2):1954 －1963.

［3］LIN Jin，PARKER R G.Analytical characterization of the unique properties of planetary gear free vibration ［J］.Journal of Vibration and Acoustics，1999，121(3):316－321.

［4］Zhu Caichao，Xu Xiangyang，Wang Haijun.Modal prediction and sensitivity analysis of wind-turbine planetary gear system with flexible planet pin［J］.Advanced Science Letters，2011，4(3):1219 －1224.

［5］赵永强，李瑰贤，常山，等.船用大功率两级人字齿行星传动系统的振动特性研究［J］.船舶力学，2009，13(4):621－627.

［6］赵永强，李瑰贤，常山，等.两级人字齿行星传动系统的模态跃迁现象［J］.吉林大学学报:工学版，2011，41(1):133－138.

［7］罗玉涛，陈营生.混合动力两级行星机构动力耦合系统动力学建模及分析［J］.机械工程学报，2012，48(5):70－75.

［8］秦大同，肖正明，王建宏.基于啮合相位分析的盾构机减速器多级行星齿轮传动动力学特性［J］.机械工程学报，2011，47(23):20 －29.

［9］秦大同，肖正明，王建宏，等.盾构机主减速器三级行星传动系统扭转动力学［J］.中国机械工程，2010，21(18):2176－2182.

［10］Montestruc A N.Influence of planet pin stiffness on load sharing in planetary gear drives［J］.Journal of Mechanical Design，2011，133(1):014501.

［11］李润方，王建军.齿轮系统动力学［M］.北京:科学出版社，1996.