五元函数全微分求积

张勇军

(海南大学信息科学技术学院，海口 570228)

全微分是多元函数微分学中的一个非常重要的概念，它反映了多元函数值的增量、各自变量的增量以及偏导数之间的关系。通过多元函数的全微分，在一定条件下可以求得满足一定关系的函数解析式，从而得出各变量之间的关系，这对于求解全微分方程所建立的数学模型是一种行之有效的方法。文献［1－5］中已给出二、三、四元函数全微分求积的概念、定义、条件、定理和方法;文献［6－12］中分别对二、三、四元函数的全微分求积问题进行了进一步的演绎、推理、归纳、总结，并给出了关于二、三、四元函数全微分求积的几种具体方法。本文在二、三、四元函数全微分求积问题的基础上，对五元函数的全微分求积问题进行研究。

1 五元函数全微分求积

1.1 五维空间曲线积分与路径无关的定义

定义 1 设 G 是一个五维空间区域:P(x，y，z，h，l)，Q(x，y，z，h，l)，R(x，y，z，h，l)，H(x，y，z，h，l)、L(x，y，z，h，l)。对于在区域G内具有一阶连续的偏导数，满足下列条件之一都成立:

① 如果对于G内任意指定的2点A，B以及G内从A到B的任意2条曲线Γ1、Γ2，则等式

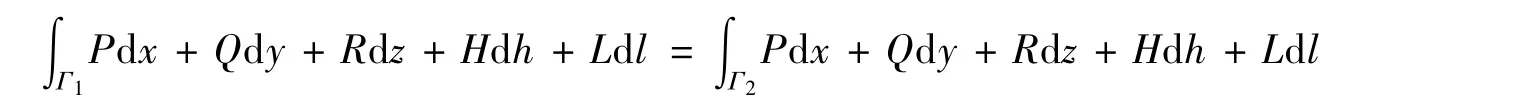
成立。

②如果沿G内任意闭曲线C的曲线积分(C在G内)有

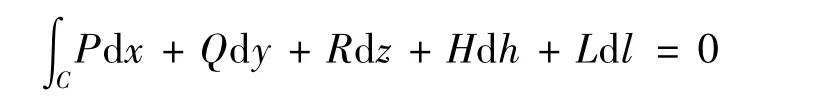
成立，则称空间曲线积分∫ΓPdx+Qdy+Rdz+Hdh+Ldl在G内与路径无关，否则与路径有关。

1.2 定理及证明

定理 1 设空间区域 G 是一个五维单连通域，函数 P(x，y，z，h，l)，Q(x，y，z，h，l)，R(x，y，z，h，l)，H(x，y，z，h，l)和 L(x，y，z，h，l)在区域 G 内具有一阶连续的偏导数，则下面的 4 个命题等价:

①对于G内的任意一条光滑(或者分段光滑)闭曲线C，满足

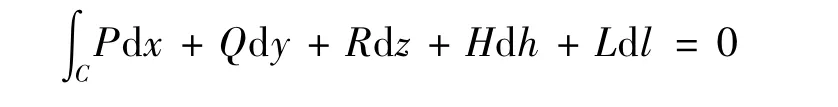
② 曲线积分∫ΓPdx+Qdy+Rdz+Hdh+Ldl与路径无关;

③ 存在 G 上的可微函数 U(x，y，z，h，l)，使得 dU=Pdx+Qdy+Rdz+Hdh+Ldl，即 Pdx+Qdy+Rdz+Hdh+Ldl为 U(x，y，z，h，l)的全微分;

证明 ①⇒②

设A，B为G内任意2点，Γ1和Γ2是G中从A到B的任意2条路径，则C=Γ1+(－Γ2)就是G中的一条封闭曲线。因此

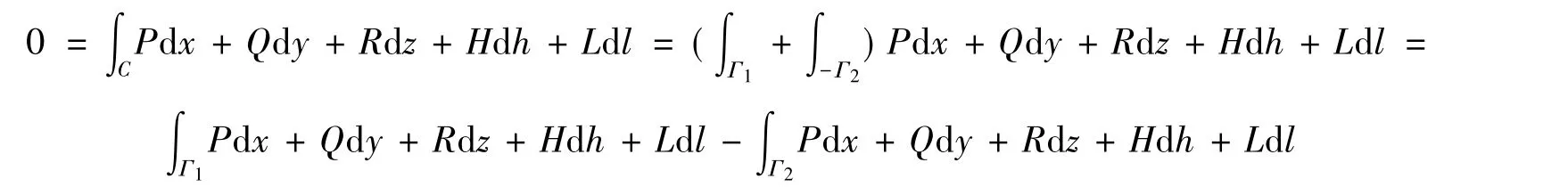
于是有

即曲线积分与路径无关。

证明 ②⇒③

取一定点(x0，y0，z0，h0，l0)∈G，作函数

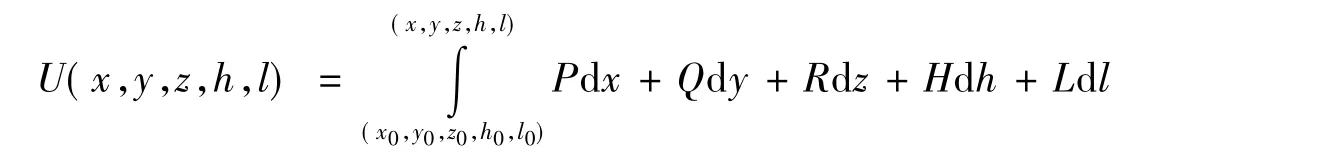
这里，沿从(x0，y0，z0，h0，l0)到(x，y，z，h，l)的任意路径积分。由于曲线积分与路径无关，因此 U(x，y，z，h，l)有确定意义。根据积分中值定理有

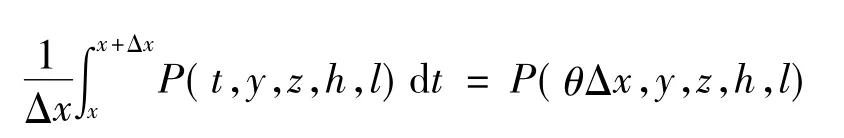
其中0＜θ＜1。因此有

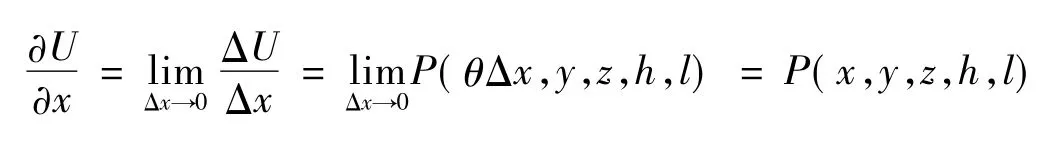
同理有

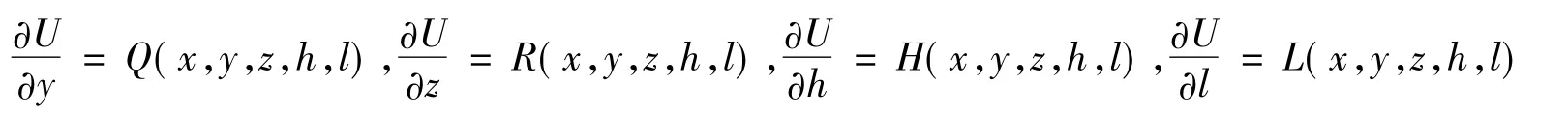
因此，在G内dU=Pdx+Qdy+Rdz+Hdh+Ldl成立。

证明 ③⇒④

因存在G上的可微函数U，使得dU=Pdx+Qdy+Rdz+Hdh+Ldl，那么

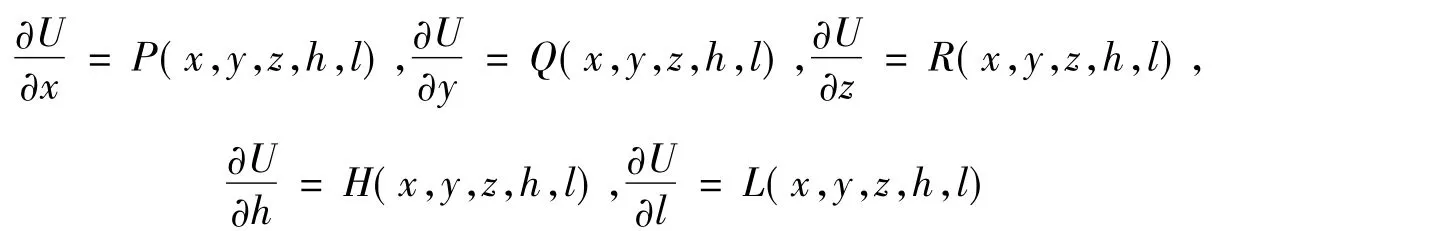
又由于函数 P(x，y，z，h，l)、Q(x，y，z，h，l)、R(x，y，z，h，l)、H(x，y，z，h，l)和 L(x，y，z，h，l)在 G 内具有 1 阶连续的偏导数，那么

证明 ④⇒①

对于包含在G内的光滑(或分段光滑)闭合曲线Γ，设它所包围的区域为～D。根据在R5中的Stokes公式得:

2 定理1成立下的五元函数解求法

2.1 空间曲线积分解求法

当定理1成立时，此函数(不计常数之差)可用下式求出

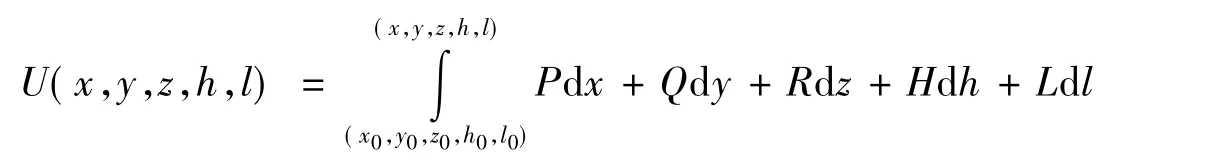
或用定积分表示为

其中 M0(x0，y0，z0，h0，l0)为 G 内某一定点，M(x，y，z，h，l)∈G。

2.2 不定积分原函数法

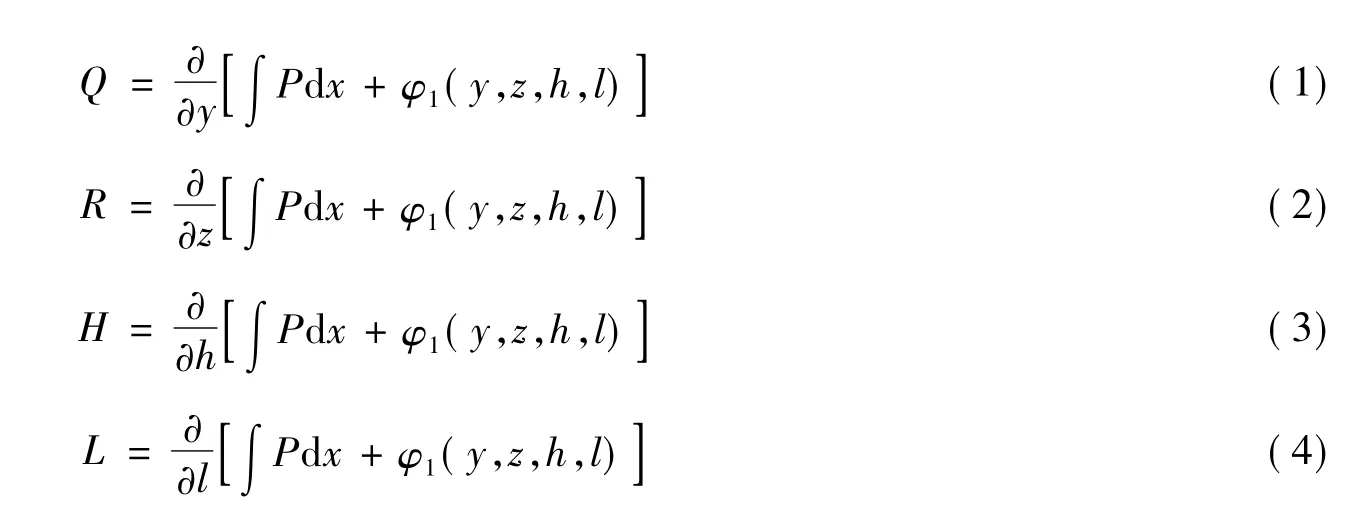
将式(1)～(4)联立方程组，可得:

又设

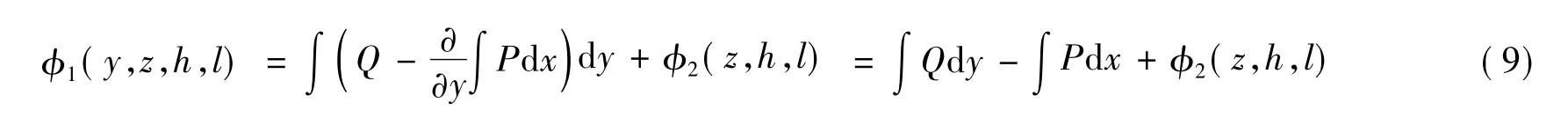
将式(9)分别代入式(6)～(8)，化简可得:

再设

将式(13)分别代入式(11)、(12)，化简得:

联立式(14)、(15)解出 φ3(h，l)，然后依次回代解出 φ2(z，h，l)，从而得出 φ1(y，z，h，l)，进而得出 U(x，y，z，h，l)。

2.3 全微分方程的分部微分法

2.3.1 凑微分法(分项组合法)

因dU=Pdx+Qdy+Rdz+Hdh+Ldl，若存在有限个函数Ui(i=1，2，…，n)属于dU=dU1+dU2+…+dUn时，则必有

其中 Pi、Qi、Ri、Hi、Li，i=1，2，…，n 为函数。

2.3.2 拆微分法(拆项微分法)

将等式dU=Pdx+Qdy+Rdz+Hdh+Ldl右边的各微分式拆开分别积分，划去相同项(相同项只取1项)即可。

3 结束语

推导了五元函数全微分求积的4种不同方法，这些方法对于一般题目的求解都可行。实际解答时，可根据题目具体特点来选择较为简洁的方法进行求解。

［1］同济大学应用数学系.高等数学:下册［M］.6版.北京:高等教育出版社，2007.

［2］同济大学应用数学系.高等数学:下册［M］.5版.北京:高等教育出版社，2002.

［3］华东师范大学数学系.数学分析:下册［M］.2版.北京:高等教育出版社，1991.

［4］华东师范大学数学系.数学分析:下册［M］.3版.北京:高等教育出版社，2001.

［5］陈纪修，於崇华，金路.数学分析:下册［M］.北京:高等教育出版社，2000.

［6］张勇军.基于四元函数全微分求积研究［J］.海南大学学报:自然科学版，2011，29(4):309－312.

［7］张勇军，智霞.基于三元函数全微分求积研究［J］.海南大学学报:自然科学版，2010，28(4):294－297.

［8］张勇军.二元函数的全微分求积［J］.重庆理工大学学报:自然科学版，2010(5):111－114.

［9］刘浩荣.关于二元函数全微分求积中积分路径的选取问题［J］.高等数学研究，1997(1):18－19.

［10］冯录祥，阎恩让.二元函数求积的一个简单方法［J］.高等数学研究，2009，12(2):48－50.

［11］资治科.全微分方程不定积分解法及其证明［J］.高等数学研究，2002(2):20－21.

［12］吴绪权.二元函数的全微分求积问题［J］.大众科学，2007(4):25.