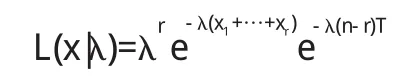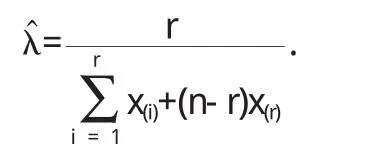基于EM算法实现混合密度极的大似然参数估计

邹小云

（湖北职业技术学院，湖北 孝感 432000）

基于EM算法实现混合密度极的大似然参数估计

邹小云

（湖北职业技术学院，湖北 孝感 432000）

在介绍极大似然估计与EM算法的基础上，探讨了基于EM算法的两混合正态分布极大似然参数估计，并举例说明了若干经典场合的极大似然估计的算法.

极大似然估计；EM算法；似然函数；参数估计

极大似然估计参数也称为最大概似估计，这就是一种概率论在统计学中的应用，同时也是参数估计的方法，它用来求一个样本集的相关概率密度函数的参数.其主要意思就是已知某随机样本满足某种概率分布，但其中具体参数还不确定，参数估计就是通过很多次反复的试验，看其结果，利用它的结果推算出参数的大概值.极大似然估计就是建立在这种思想上：已知某个参数能使这个样本出现的概率最大，我们自然就不会再去选择其他小概率的样本，所以就把这个参数作为估计的真实值，这种算法就是EM的模型.付淑群给出了《EM算法正确收敛性的探讨》的文章；李述山给出了《两混合分布的一种参数统计方法》[1]的文章；杨珂玲,韩惠芳给出了《两混合正态分布的参数统计方法》[2]的文章.本文在介绍一般极大似然估计法和EM算法的基础上，综述了文献[1],[2],[3]的结果，并给出了几个极大似然估计算法的实例.

1 极大似然估计

定义1[4]设总体X的概率函数为f(x|θ)，其中θ={θ1,…, θm}为未知参数，θ∈Θ.设x=(x1,…,xN)，是来自X的简单随机样本，令

称作为θ的函数L(θ|x)为似然函数.

定义2[4]在定义1的记号下,若(x)是θ的一个估计量，满足条件

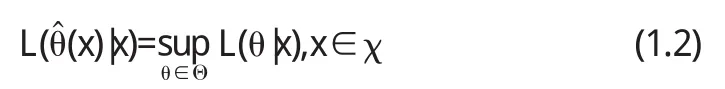
概率函数大都具有指数函数的形式，采用似然函数的对数求解通常更加简便.称

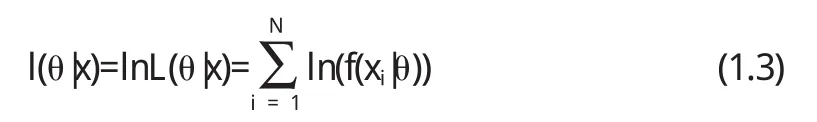
为对数似然函数.因为对数变换是严格单调的，所以lnL (θ|x)与L(θ|x)在求极大值的时候是等价的.因此通常将(1.3)式分别对θi求偏导，并令期值为零，得到似然方程组如下:

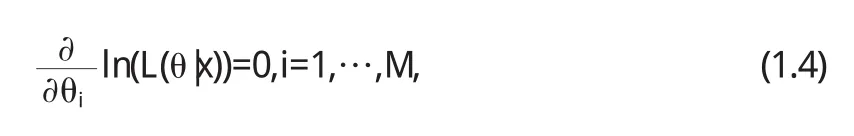
按上面介绍的思想又会存在一些问题：对于很多具体情况不能构造似然函数解析表达式，或似然函数表达式过于复杂，导致求解方程组(1.4)很困难.必须借助其它方法，其中EM算法就是在实际应用中的一种广泛且有效方法.

2 极大似然估计的算法

2.1 常规算法

通过对似然函数L(x|θ)或对数似然函数lnL(x|θ)求导而得到似然方程

得似然方程的解，验证其解从而得极大似然估计.

一般说来，我们并不要求似然函数一定关于θ可微，如果它关于θ可微，则往往用求似然方程的根来求解θ的M L E.要指出的是似然方程的根不一定是MLE，反过来，似然方程若无根，也可能有M L E存在.

2.2 极大似然估计的EM算法

2.2.1 EM算法

EM算法主要应用在缺失数据条件下的参数估计，是进行极大似然估计时的一种有效方法.根据EM算法的特点，我们可以在观测数据的基础上添加一些“潜在数据”，从而简化计算过程，完成一系列简单的极大化或者模拟.

假设Y为服从某一分布的非完全观测数据，Z为缺失数据，则完全数据X=(Y,Z)，由乘法公式，X的概率函数f(x|θ)与Y的概率函数f(y|θ)及Z的概率函数f(z|θ)的关系为

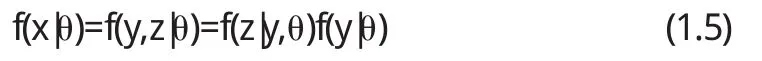
由(1.5)式给出的X,Y,Z概率函数之间的关系，可以得到新的函数

则称此函数为完全数据X的似然函数，但是由于隐变量未知，导致似然函数L(θ/X)是随机的，并且由Z决定，这样我们用不完全数据Y来估计参数θ的极大似然估计准则如下：

EM算法第一步(E-step)是给定观测数据Y和当前参数估计初值，来计算完全数据对数似然函数lnf(Y,Z|θ)，关于未知数据Z的条件期望，定义对数似然函数的期望

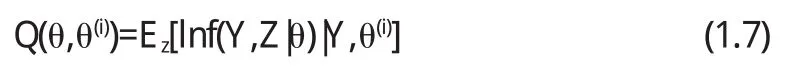
其中θ(i)为已知当前的参数估计值.在(1.7)式中Y和θ(i)都为常数，θ为待优化参数，Z为随机变量，并且假设它服从某一分布f(z|Y,θ(i))，因此(1.7)式可写作为

其中f(z|Y,θ(i))是未知数据Z的边缘分布的密度函数，且依赖于观测数据Y和当前参数θ(i)，D为Z的取值空间.由乘法公式可得

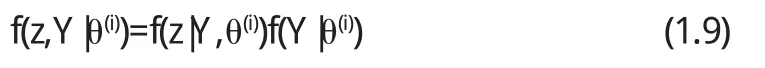
由于f(y|θ(i))与θ无关，因此在实际过程中f(z,Y|θ(i))用来代替f(z|Y,θ(i))并不影响(1.8)式中似然函数的最优化.

EM算法第二步(M-s t e p)：最大化期望Q(θ,θ(i))，即找到一个θ(i+1)使之满足

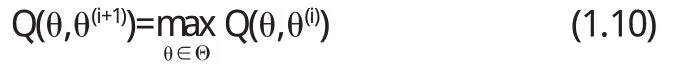
如此进行依此迭代θ(i)→θ(i+1)，将上述E步和M步进行迭代下去直到||θ(i)-θ(i+1)||或Q(θ,θ(i+1))-Q(θ,θ(i))充分小为止.

2.2.2 混合正态分布参数极大似然估计的EM算法

下面我们就两混合正态分布参数的极大似然估计问题来证明极大似然估计的EM算法

设观测样本X=(x1,x2,…,xN)是从两正态混合密度

(其中θ=(α1,θ1,θ2),α1+α2=1且f1,f2为正态分布的密度函数,θ1, θ2为分布参数)的总体中独立抽取的，则观测样本的对数似然函数表达式为

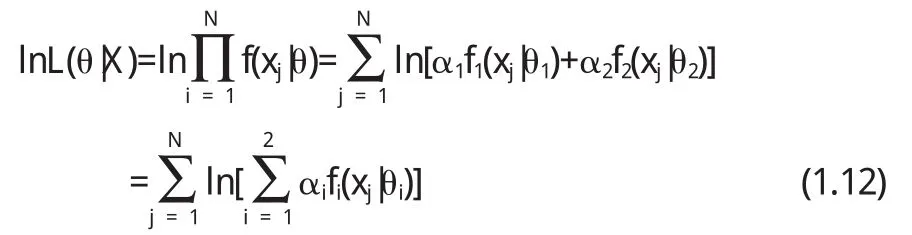
下面就于EM算法来求解两混合正态密度的极大似然估计.

假设Y为观测数据，Z为遗失数据，则完全数据X=(Y, Z).因为遗失数据Z未知，假定Z为随机变量，所以要确定Z的分布

则Zj=(Z1j,Z2j)T,Xj=(Yj,ZjT).

在一次观测中，有两种结果，每种结果的概率为α1,α2，所以

Zj～，其中Z1,Z2,…ZN独立同分布，从而

则完全数据的对数似然函数为

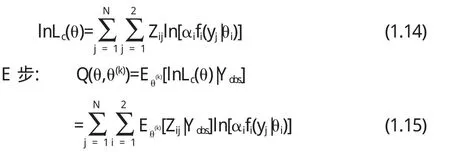
其中Yobs指Y的观测数据，θ(k)表示当前参数，令

M步：极大化Q(θ,θ(k))，并用极大值点处的θ代替θ(k)作为下一轮循环的迭代的初始值，在极大化(1.1 7)式时只需要极大化含αi和θi的项即可.为了估计αi我们可引入拉格朗日乘法，约束条件为.故

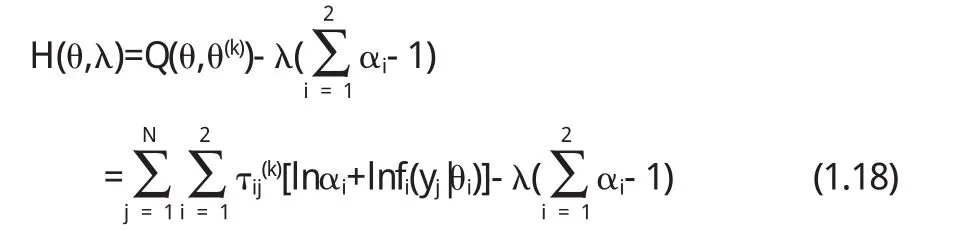
两边分别对αi,θi,λ求偏导.解方程组可得

假如混合分布中的两部分为d维多元正态分布，则概率密度函数为

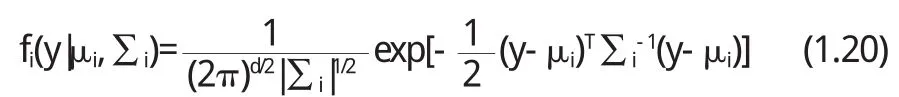
把(1.2 0)代入(1.1 7)中，忽略与θi无关的项得

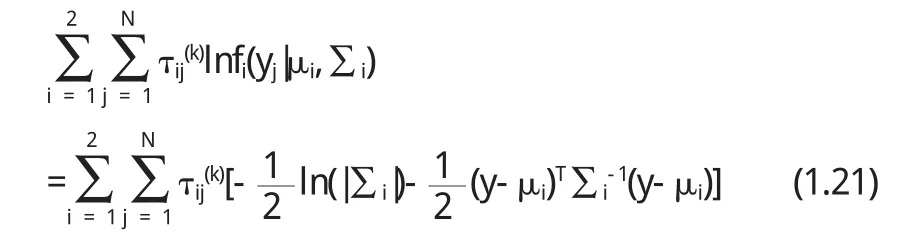
对上式关于μi求偏导并令其为0得：

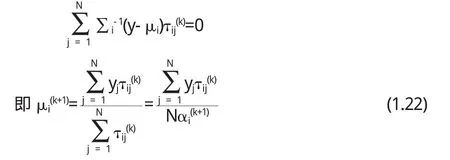
我们改写(1.2 1)式得

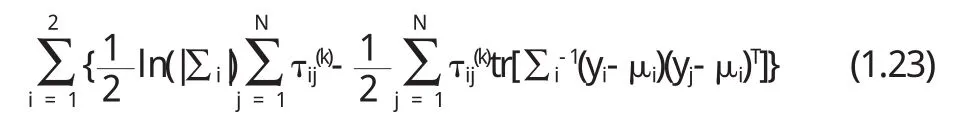
因此一次过程由式(1.19)，(1.22)，(1.24)实现.

将求得的参数值θ(k+1)代替θ(k)开始下一轮迭代，将最终收敛到极大似然估计值代入对数似然方程，即可获得对数似然函数的极大值.

3 若干经典场合的极大似然估计的算法

例1 设X1,…,Xn是来自B(1,θ)的一个样本，0<θ<1.求参数θ的极大似然估计.

解 因为P(X=k)=θk(1-θ)1-k,k=0,1，所以θ的似然函数为

对数似然函数为

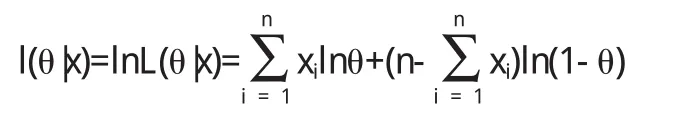
例2 设X1,…,Xn为取自Poisson分布P(λ)总体的简单随机样本，求参数λ的极大似然估计.

解 因为似然函数为

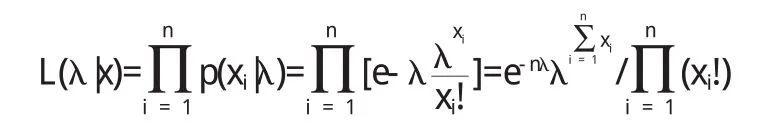
所以对数似然函数为

易验证l"(λ|x)<0,所以上式中的λ^即为l(λ|x)唯一的最大值点，即为λ的极大似然估计.

例3 (定数截尾寿命实验)设某种电子元件，由于种种随机因素的干扰，其寿命不同，抽取n个作试验，设元件寿命的分布为

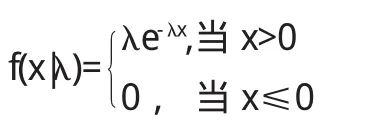
指定一个时刻T>0.实验进行到全部抽出的n个元件都失效，或到时刻T为止.记Xi=元件i的寿命或T，视元件在时刻T时已失效或否而定，要由X1,…,Xn作λ的极大似然估计.

若xi

对数似然函数为

似然方程的根为

这λ即为的极大似然估计.

在以上的例子中,许多常用的分布如正态分布,Bernoulli分布,Poisson分布等其参数的极大似然估计和矩估计是一致的,但也有许多情况如均匀分布,其参数的极大似然估计和矩估计并不同,而进一步比较往往是极大似然估计有更多的优良性,对于许多估计问题,求极大似然估计或似然方程的解,往往无法得到明显的表达式,所以在实际数据分析中常用的做法是用各种最有化算法求得极大似然估计的值,其中EM算法就是极大似然估计的一种有效方法.

〔1〕付淑群.EM算法正确收敛性的探讨[J].汕头:汕头大学学报,2002.1～12.

〔2〕李述山.两混合分布的一种参数统计方法[J].山东轻工业学报,1999.73～77.

〔3〕杨珂玲,韩慧芳.两混合正态分布的参数估计方法[J].黄冈师范学院学报,2006.16～19.

〔4〕陈希孺.数理统计引论[M].北京:科学出版社,1988.55～56.

〔5〕茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006.115～116.

O212

A

1673-260X（2013）12-0008-03