PSO-PID 控制器在发酵工程中的应用
2013-07-31金连龙屈宝存
金连龙,屈宝存
(辽宁石油化工大学, 辽宁 抚顺 113001)
发酵工程的各个变量互相制约,互相影响,共同决定发酵效果,这就决定了发酵过程是具有强非线性,造成了对其进行优化和控制较为困难[1,2]。发酵的效果直接影响了工程的效益,为了保证和提高产品质量,尽可能选择鲁棒性强和简单的控制器,这也是PID 控制器广泛使用的原因。其中重要的一点就是要通过参数整定的方法来获得良好的PID 参数,而稳定高效的PID 参数整定方法是我们现在一直在研究的[3]。
目前,已有超过200 种PID 控制器参数的整定方法,包括临界比例法,衰减曲线法,反应曲线法等等。一般的参数整定方法依赖经验,当对鲁棒性和快速性要求较高时,很难获得满足要求最佳 PID参数。包括遗传算法在内的一些人工智能方法具有结构简单,收敛速度快的优点,这为PID 控制器优化带来了更好的方法。但是,过早收敛是遗传算法的问题,其搜索能力会在优化具有参数相关性强的对象时变差。
粒子群优化(particle swarm optimization)算法是一种基于群智能(swarm intelligence)方法的演化计算(evolutionary computation)技术[1]。可用于优化多峰值、非线性和不可微的复杂函数,由于具有算法简单、可调参数较少、容易实现和效果明显等优点,获得了广泛的应用。发酵过程恰恰是一个非线性的复杂控制对象,还很少有智能优化的PID 控制器用于该过程。笔者针对发酵过程中的一个问题,使用粒子群优化PID 控制器参数,从而获得更好的控制效果,以提高发酵过程的质量。
1 粒子群优化算法的基本原理
粒子群优化算法(Particle Swarm optimization)又翻译为粒子群算法、粒子群算法、或粒子群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能 (Swarm intelligence, SI) 的一种。PSO 算法最初以图形方式模拟鸟群优美的不可预知的运动。通过观察动物的社会行为,社会共享的发现,提供了一个进化上的优势,并以此作为算法的开发基础。加入相邻的速度匹配,并考虑了加速的距离和多维搜索,形成了最初版本的粒子群优化算法。之后引入惯性权重 w,用来更好地控制开发(exploitation)和探索(exploration),形成的标准版本[4]。基于PSO算法的群体,根据个体对环境的适应程度,将其移动到最佳区域。然而,它不使用演化算子的,但每个个体作为一个 D 维的搜索空间的体积的粒子(点),以一定的速度在搜索空间中飞行,这是根据自己的飞行速度和同伴的飞行经验进行动态调整这个速度根据它本身的速度和同伴的飞行经验来进行动态调整[4]。第 i 个粒子表示为 Zi= (Zi1, Zi2, …, ZiD),它所经过的最佳位置(最佳适应值)记为Xi= (Xi1,Xi2, …, XiD),也称之为Xbest。用g 来表示群体中所有粒子经历过的最佳位置的索引号,即Xg,也称为gbest。Si= (Si1, Si2, …, SiD)表示粒子的速度。每一代中,它的第d 维(1 ≤ d ≤ D)的改变,根据下面的等式改变:
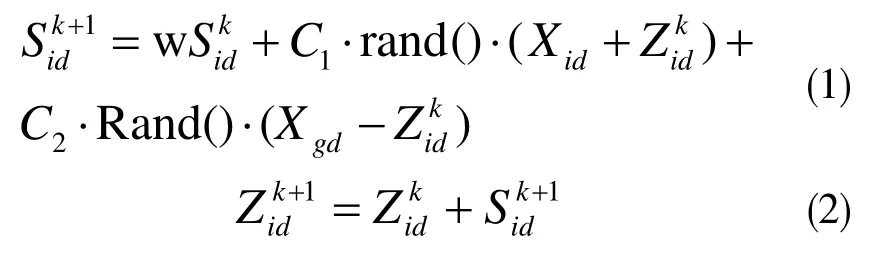
其中, w 为惯性权重(inertia weight),C1和C2为加速常数(acceleration constants),rand( )和Rand( )分别是在[0,1]范围内变化的随机数。
此外,Smax是粒子的速度Si的上限。如果粒子当前的速度使得它的速度 Si,d超过在某维度的最大速度Smax,d,则限制Smax,d为该维度的最大速度。
对公式(1),粒子先前行为的惯性为第1 部分,第2 部分是“认知(cognition)”,即粒子本身的思考;“社会(social)”为第3 部分,它表示跨粒子的信息共享与相互合作。
“认知”部分可以由Thorndike 的效应法则(law of effect)所解释,即一个得到加强的随机行为在将来更有可能出现。这里的行为即“认知”,并假设获得正确的知识是得到加强的,这样的一个模型假定微粒被激励着去减小误差[5]。
“社会” 部分可以由 Bandura 的替代强化(vicarious reinforcement)所解释。根据该理论的预期,当观察者观察到一个模型在加强某一行为时,将增加它实行该行为的几率。即微粒本身的认知将被其它微粒所模仿[5]。
粒子群优化算法使用如下心理学假设:在寻求一致的认知过程中,个体往往记住自身的信念,并同时考虑同事们的信念。当其察觉同事的信念较好的时候,将进行适应性地调整。标准PSO 的算法流程如下:
初始化一群粒子(群体规模为m),包括随机的位置和速度[6];
评价每个粒子的适应度;
对每个粒子,将它的适应值和它经历过的最好位置 xbest 的作比较,如果较好,则将其作为当前的最好位置xbest;
对每个粒子,将它的适应值和全局所经历最好位置gbest 的作比较,如果较好,则重新设置gbest的索引号[6];
根据方程(1)变化粒子的速度和位置;
如未达到结束条件(通常为足够好的适应值或达到一个预设最大代数Gmax),回到(2)[6]。
2 发酵工程的仿真和讨论
2.1 发酵工程
被研究的发酵过程由如下的微分方程描述的:

式中:V—稀释率;
X—菌体质量浓度;
S—底物质量浓度;
Sf—流加底物质量浓度;
P—产物质量浓度;
µ—比生长率,表现出典型的底物和产物抑制;
µmax=最大比生长速率;
Pm—产物饱和常数;
Km—底物饱和常数;
YX/S—菌体对底物的得率系数;
α,β—动力学参数,其参数值和发酵操作条件见参考文献[7]。
V—通常作为调节变量;
X,S,P—都可作为输出变量。
文献[7]的研究表明,通过合理的控制变量X 能够获得最佳的生产能力。所以,本文选择X 作为被控对象。
2.2 仿真结果及讨论
图1 给出了发酵过程的示意图,发酵工程常常表现出生长率不一致的多阶段特性,菌体质量浓度在不同区间有不同的生长特点,即使采用IMC 的方法整定的PID 控制器参数,也无法完全满足各个阶段的控制要求[8]。因为菌体质量浓度与最终的产物收率密切相关,所以,采用将发酵过程划分为3 个连续子过程,分别使用粒子群优化算法优化每个阶段的PID参数,这样就获得了3个子区间的基于PSO优化的PID 控制器。
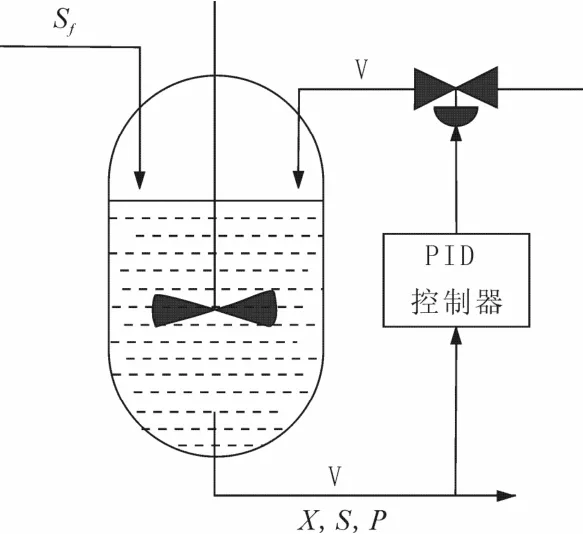
图1 发酵过程PID 控制系统Fig.1 Fermentation process PID control system
通过仿真进行比较,笔者把采用 IMC 优化的PID 控制器记为 PID,把采用粒子群算法优化的 PID控制器记为PSO-PID。由于高频率大幅度的调节执行阀会降低其使用寿命。所以,约束调节变量V 的变动范围调整到±0.5。
PID 和PSO-PID 控制器在有噪声和无噪声(理想状态下,实际操作用不存在无噪声情况,可视为噪声很小的情况)两种过程情况下在不同质量浓度阶段的菌体质量浓度的控制性能比较见表 1。控制器的性能指标采用常用的ISE(integral square error)误差平方积分指标。
当在无噪声干扰过程下,菌体质量浓度在高中低三种质量浓度下的控制结果的比较分别如图 2-4所示。PSO-PID 控制其的性能要明显优于普通PID控制器。当在有噪声干扰过程下,菌体质量浓度在三种质量浓度下的控制结果分别如图5-7 所示。在有噪声干扰下依然是PSO-PID 控制器的表现最佳。由于在控制各质量浓度区间的开始,都有偏向高质量浓度的趋势。在此发酵过程中,PSO-PID 控制器在各子区间都进行了优化,因此其在各区间的参数是不同的。所以采用PSO-PID 控制器的方案是最优的。

表1 两种PID 控制器在不同浓度区间的控制结果对比Table 1 Two PID controller in the control result of the different concentration ranges comparison kg/m2
3 总 结
通过仿真实验表明,PSO-PID 控制器的控制效果是要优于传统的PID 控制器的。这种具有进化能力的优化算法的应用对发酵过程有着十分重要的现实意义和应用价值。
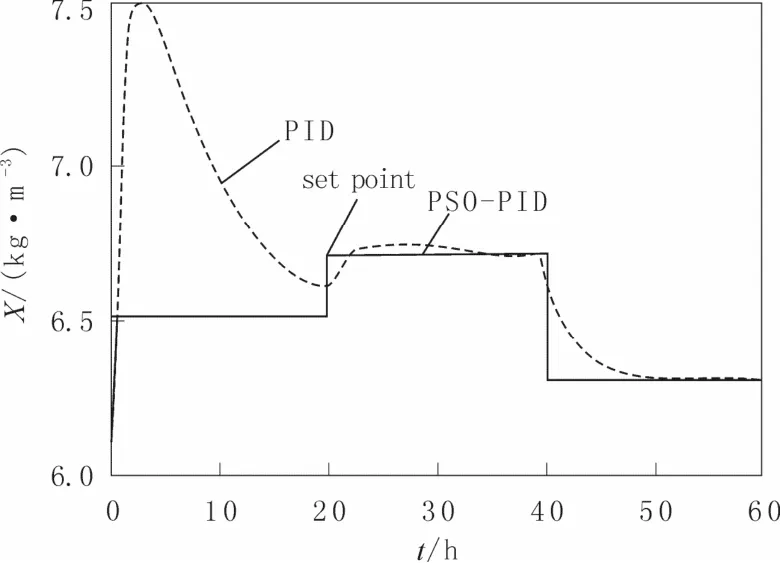
图2 PSO-PID 和PID 控制方法性能比较(高质量浓度下无噪声)Fig.2 Control method for performance comparison of PSO-PID and PID(No noise and high concentration)
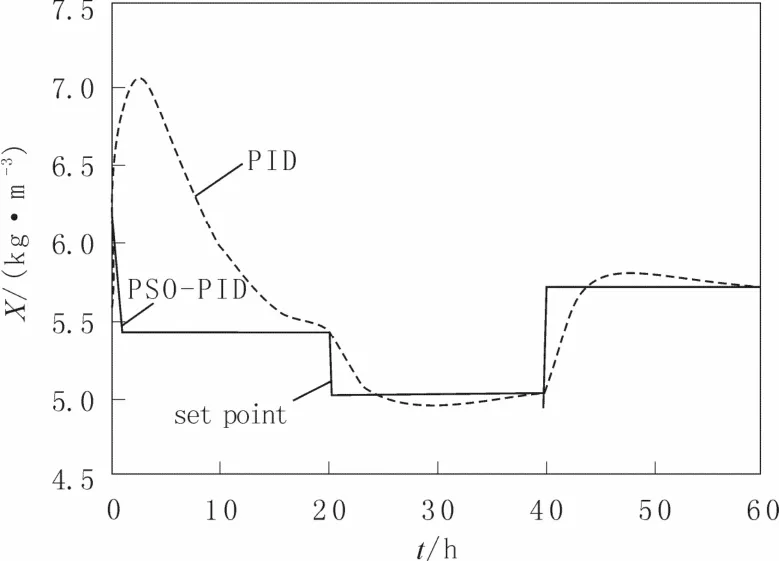
图3 PSO-PID 和PID 控制方法性能比较(中质量浓度下无噪声)Fig.3 Control method for performance comparison of PSO-PID and PID(No noise and normal concentration)

图4 PSO-PID 和PID 控制方法性能比较(低质量浓度下无噪声)Fig.4 Control method for performance comparison of PSO-PID and PID(No noise and low concentration)

图5 PSO-PID 和PID 控制方法性能比较(高质量浓度下有噪声)Fig.5 Control method for performance comparison of PSO-PID and PID(Noise and high concentration)
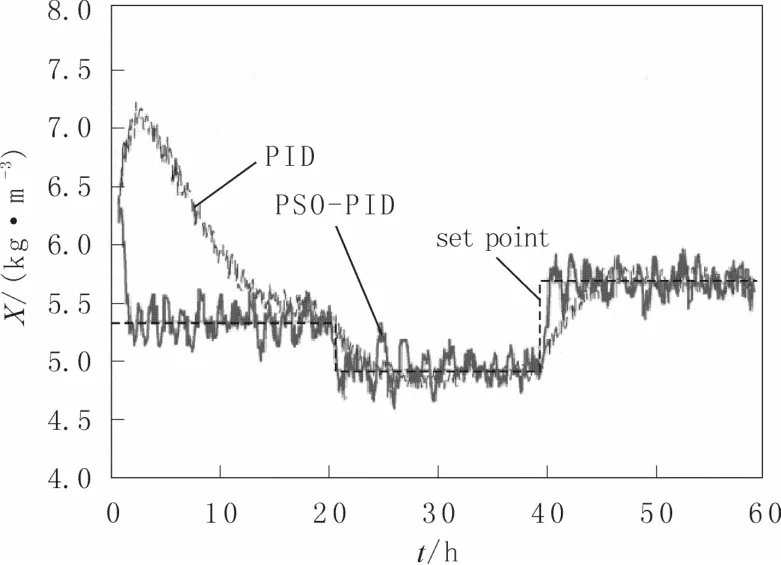
图6 PSO-PID 和PID 控制方法性能比较(中质量浓度下有噪声)Fig.6 Control method for performance comparison of PSO-PID and PID(Noise and normal concentration)
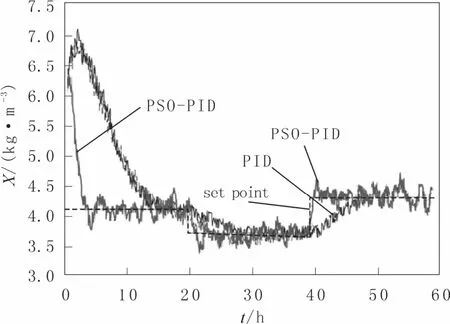
图7 PSO-PID 和PID 控制方法性能比较(低质量浓度下有噪声) 。Fig.7 Control method for performance comparison of PSO-PID and PID(Noise and low concentration)
[1] 陈坚, 李寅.发酵过程优化原理与实践[M]. 北京:化学工业出版社,2002.
[2] 史仲平, 潘丰.控制与检测技术[M]. 北京:化学工业出版社现代生物技术与医药科技出版中心, 2005.
[3] 王介生, 王金城, 王伟. 基于粒子群算法的 PID 控制器参数自整定[J]. 控制与决策, 2005, 20(1): 73-76.
[4] 石琴, 王楠楠, 仇多洋. 粒子群优化的模糊聚类方法在车辆行驶工况中的应用[J]. 中国管理科学, 2011, 19(2): 110-115.
[5] 吴平健. 进化多目标优化方法研究及在空战决策中的应用[D]. 长沙:湖南大学, 2009.
[6] 董殿敏. 微粒群算法在动态优化中的应用研究[D]. 太原:太原科技大学, 2009.
[7] Henson M A, Seborg D E. An internal model control strategy for nonlinear systems[J]. AIChE journal, 1991, 37(7): 1065-1081.
[8] Radhakrishnan T K, Sundaram S, Chidambaram M. Non-linear control of continuous bioreactors[J]. Bioprocess and Biosystems Engineering,1999, 20(2): 173-178.
