圆形无压隧洞水面线解析计算模型

滕 凯 李新宇

(1.齐齐哈尔市水务局，黑龙江 齐齐哈尔 161006;2.大连交通大学，辽宁 大连 116021)

圆形断面隧洞在水利水电供排水工程中应用广泛，由于受进、出口水位条件的限制，在洞内常常产生属于恒定渐变流条件的降水或壅水水面线，因此，圆形断面隧洞水面线计算是工程设计及运行管理中必须完成的一项重要工作。目前，工程上通常采用的水面线计算方法主要有分段求和差分试算法［1-2］、迭代法[3-4]和图解法[5]。这些方法均是以能量方程为基础，通过分段计算逐级推求下一个(或上一个)断面水位为基本思路来实现的，因此，这些方法均存在误差累积和计算繁复问题。而由于圆形断面隧洞的水力要素为含三角函数的超越方程，加之恒定渐变流水面线计算方程自身的隐含性，使得圆形断面隧洞内水面线计算变得更加复杂。为改进目前常规计算方法存在的问题，参考文献6 基于恒定渐变流基本微分方程，采用数值分析理论，得到了含流程S 与始、末端水深h1、h2的解析计算公式，利用该公式可直接完成沿程水面线计算，但因该公式适用范围小(仅适用于0.2≤x≤0.8，x 为充满度)，且在此范围内计算参数需按3 个分段区间分别选取，不便实际应用，而且最大替代误差达2.5%。

为了解决目前圆形断面隧洞水面线计算存在的问题，本文依据优化拟合原理，取目标函数为标准剩余差最小，经逐次逼近拟合计算，获得了在工程实用范围内用一个近似可积分函数替代原积分中不可积函数，并通过简单积分得到含有流程S 及首、末端水深h1、h2的简化解析计算通式，使求解该种断面水面线的计算过程更加简捷、直观，便于实际应用。

1 圆形断面隧洞水面线基本方程

由连续方程和能量方程表示的无压圆形断面恒定渐变流水面线数学模型为［5］

其中

1.1 断面水力要素

圆形过水断面(见图1)的水力要素为

以上式中:θ 为与水深h 相对应的圆心角，rad;d 为圆形断面直径，m。由式(5)经整理可得圆心角为

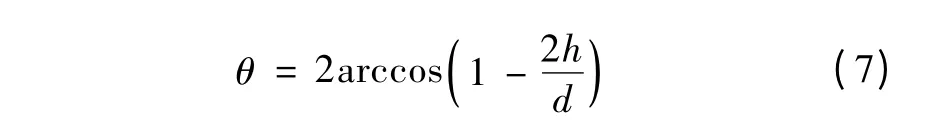
图1 无压流圆形断面

1.2 水面线基本方程

将圆形断面水力要素式(2) ～式(7)分别代入式(1)，并设

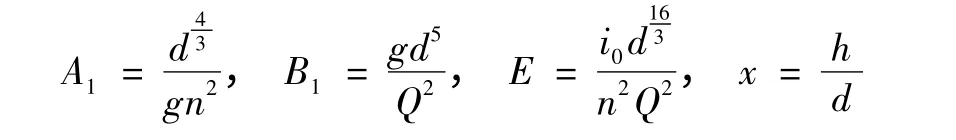
经进一步整理即可获得求解圆形断面隧洞水面线的基本公式为

其中

以上式中:A1、B1、E 均为已知综合参数;J'、Fr'2均为计算断面无量纲中间变量;x 为计算断面无量纲水深。

由式(9)、式(10)可见，x 的取值范围为［0，1］，而在实际工程中，x ＜0.15 的情况极为少见;同时，考虑为避免洞内产生不稳定的半有压流现象，《水工隧洞设计规范》［7］规定，洞内水面线以上的富余空间面积不宜小于隧洞断面积的15%，且净空高度不应小于0.4m，由此可以求得x ＜0.793，本文考虑实际应用中始、末端可能出现特殊水深，将x 的取值范围外延为［0.15，0.85］。

2 圆形断面隧洞水面线近似计算公式的建立及精度分析

2.1 解析计算模型的建立

因式(8)为分别含有J' 及Fr'2［即公式(9)、式(10)］两个未知量为x 的无量纲超越方程的积分函数，无法通过常规的数学方法直接获解。为解决这一复杂方程的积分求解问题，在工程实用参数范围内(即0.15 ≤x ≤0.85)，假定函数J″ = f(x)、Fr″2=f(x)可以分别替代式(9)及式(10)，并满足以下条件:

(1)要有较好的拟合替代精度，以确保水面线的最终成果满足工程设计要求。

(2)拟合替代公式的表达形式应最简洁化。

(3)该拟合式代入式(8)后，应满足用常规的数学方法完成积分的要求。

依据式(9)、式(10)即可通过设定不同的x分别求得J'及Fr'2，分别展绘J'—x 及Fr'2—x 关系曲线，如图2 所示。

图2 J—x 及Fr2—x 关系曲线

由线图2 可见，J'—x 及Fr'2—x 具有较好的高次反比例函数关系，据此，经多组备选函数的数值拟合分析及回归计算，以标准剩余差最小为最终希望目标函数［8-11］，即

式中:y'i、yi分别为拟合近似值及理论值;n 为拟合计算的数组数。

经逐次逼近拟合［12-13］即可获得如下替代函数，即

将式(11)、式(12)代入式(8)经整理并取积分可得

其中

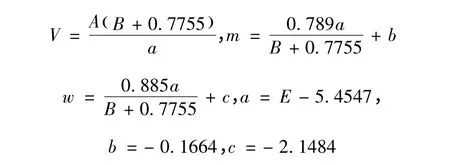
以上式中:V、m、w 及a 均为中间已知参数;J″、Fr″2分别为J' 及Fr'2的拟合替代值;b、c 均为已知常数。

在工程适用范围内，因a = E－5.4547 ＞0，则b2－4ac ＞0，完成式(12)中的积分可得

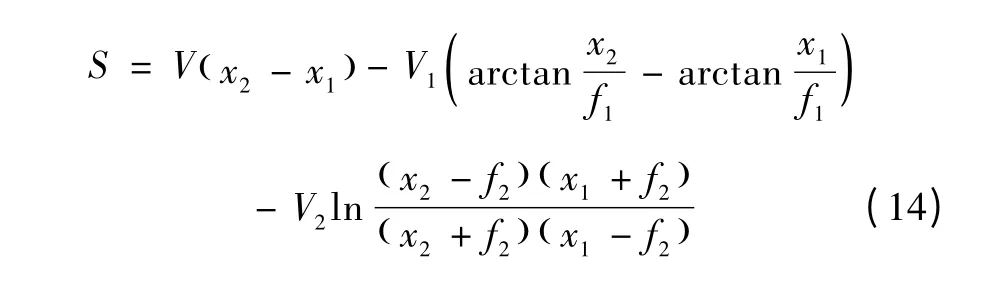
其中:

以上式中:f1、f2、V1及V2均为中间参数;x1、x2分别为已知和待求无量纲水深。

利用式 (14)即可根据已知参数Q、n、i0、r1及h1(或h2)求解出水深为h2(或h1)情况下所对应的流程S ，较《水工隧洞规范》推荐的分段求和法更加简单和直接，同时，也避免了因分段求和法所产生的误差累积。

2.2 拟合误差分析

为分析利用式(14)进行水面线计算的精度问题，先对式(11)及式(12)分别拟合式(9)及式(10)的替代精度进行分析。在工程实用参数范围内(0.15≤x≤0.85)，可选取不同的xi分别代入式(9)～式(12)即可分别 求 得J'、Fr'2及J″、Fr″2，并用式(15)完成拟合相对误差计算，计算结果见表1、表2。

式中:zi为拟合相对误差%;i 为在拟合计算中所选取的第i 个数据。

表1 式(11)拟合精度比较

表2 式(12)拟合精度比较

由精度比较表1、表2 可见，在工程实用参数范围内，用式 (11)、式(12)分别替代式 (9)、式(10)的最大拟合替代相对正、负误差分别为:式(11)为1.736%和－2.290%;式(12)为1.483%和－0.442%;且最大拟合相对误差均出现在常用区域边缘，在工程常用区域内，最大拟合误差小于1.762%，平均拟合相对误差分别为:式 (11)为0.074%;式 (12) 为 0.030%。由 此 可 见，式(11)、式(12)具有较高的拟合替代精度，完全可以满足实际工程的设计精度要求。

由于水面线计算公式为拟合替代函数的积分求和所得，而在求和后因正、负误差的相互抵消，可使最终水面线的计算成果精度进一步提高。因此，本文方法获得的水面线成果将更接近理论值。

3 应用举例

已知某输水隧洞为圆形断面，半径r =1.5m，洞底设计坡降i=0.013，洞内壁糙率系数n=0.015，设计流量Q=23.37m3/s，起始水深h1=1.9m。试计算沿程水面线(洞长为1.0km)。

根据明渠均匀流计算方法可求得洞内的临界水深hk=2.11m，正常水深h0=1.547m，因h0＜h ＜hk，洞内属降水水面线。取末端计算水深 h2=h0( 1 +1% )= 1.56m，利用本文公式可分别求得:f1=0.50798，f2= 0.51313，V = 318.652，V1=－79.389，V2= 85.322，x1= 0.6333，x2= 0.52，将其分别代入式(13)即可求得流程S 为

为比较本文公式计算成果的精度，采用分段求和法完成水面线计算，取3 个分段、6 个分段和9 个分段分别求得对应末端水深h2=1.56m 时的流程S 分别为172.68m、188.92m 和197.13m。由于分段求和法存在同号误差，因此随着分段数的增加，其水面线的计算成果逐渐接近理论水面线。可见，本文公式所求成果与常规的取9 个分段求和成果基本一致(相对误差仅为2.89%)，本文公式具有较好的计算精度。

4 结 语

采用常规的分段求和法计算圆形过水横断面隧洞内水面线十分繁琐。本文依据优化拟合理论，将积分内不可积分函数用可积分函数替代， 获得了可直接完成圆形断面隧洞内水面线求解的近似计算通式，它具有以下优点:

(1)简化公式在工程实用参数范围内不分段，可使水面线计算由一个表达简明的计算通式完成，避免了分段公式在求解计算中所带来的诸多不便。

(2)公式中的系数均为常数，可非常简捷地由已知水深h1计算出对应水深h2情况下的流程S，进而完成水面线计算，实现了计算简单、快捷，有效提高了工作效率，具有实际应用推广价值。

(3)由于分段求和法无论壅水还是降水水面线均存在同号误差，最终造成误差累积，影响成果精度，因此，只能通过增加分段数量来提高计算精度，而增加分段数量又使计算工作量增大。本文计算公式为通过对原函数的高精度替代并积分所得，因此，由于正、负替代误差的相互抵消，较好地解决了误差累积问题，使水面线计算成果的精度进一步提高。

［1］ 武汉大学水利水电学院，水力计算手册［M］.北京:中国水利水电出版社，2006:60-80.

［2］ 水工设计手册［M］.2 版.北京:中国水利水电出版社，2011.

［3］ 张建民，王玉蓉，许唯临.恒定渐变流水面线计算的一种迭代方法［J］.水利学报，2005(4):501-504.

［4］ 万五一，江春波，李玉柱.变步长法在天然河道水面线计算中的应用［J］.哈尔滨工业大学学报，2007(4):648-650.

［5］ 清华大学水力学教研室.水力学［M］.北京:高等教育出版社，1980.

［6］ 黄朝煊.圆形无压隧洞恒定渐变流水面线计算的近似法［J］.灌溉排水学报，2012(5):113-117.

［7］ DL/T 5195—2004 水工隧洞设计规范［S］.北京:中国水利水电出版社，2003.

［8］ 刘刚，滕凯.梯形断面均匀流水深的近似计算公式［J］.水利与建筑工程学报，2012，(1):41-44.

［9］ 谢成玉，滕凯.三次抛物线形渠道断面收缩水深的简化计算［J］.南水北调与水利科技，2012(2):148-150.

［10］ 谢成玉，滕凯.抛物线形断面渠道均匀流水深的近似计算公式［J］.水电能源科学，2012(7):94 ～95，172.

［11］ 滕凯.消力池深的简化计算法［J］.人民长江，2012(15):77-79，91.

［12］ 王慧文.偏最小二乘回归法及其应用［M］.北京:国防工业出版社，1999.

［13］ 阎凤文.测量数据处理方法［M］.北京:原子能出版社，1988.