电磁学与电动力学中的磁单极－I

王 青

（清华大学物理系，北京 100084）

1 关于磁单极子

磁单极子是指一些仅带有南极或北极单一磁极的磁性物质.在电磁学和电动力学中它是作为类比于电相互作用源的电荷对应针对磁相互作用的源而出现在物理中的.早在1931年英国物理学家狄拉克就利用数学公式预言了磁单极子的存在.当时他认为，既然带有基本电荷的电子在宇宙中存在，那么理应有带有基本磁荷的粒子存在.遗憾的是在现实世界中至今为止尚未发现磁单极子，而只看到正反磁荷靠的很近形成的磁耦极子.在著名的麦克斯韦方程组中，这体现为真空中的麦克斯韦方程组的右端没有出现相应的源磁荷密度项和磁流密度项.即使这样，在物质材料的磁性质描述中，人们还是经常喜欢采用等效磁荷的方法进行讨论和计算.理论物理学家和实验物理学家们还在大胆地想象和探索各种可能的磁单极及其相应的物理和应用.特别是实验物理学家们仍在孜孜不倦持续、积极、认真地寻找磁单极.虽然基本的磁单极粒子一直未能被发现，但层展意义的磁单极的研究进展确不断有所报道.例如2010年10月17日自然物理子刊（DOI：10.1038／NPHYS1794）报道科学家在人工戈薇的自旋冰中观察到实空间层展的磁单极及相关的狄拉克弦（将在下一篇文章介绍和讨论狄拉克弦）.2013年6月6日，美国每日科学网站报道，德国科学家通过将磁铁表面细小的磁尖混合在一起制造出了一个人造磁单极，研究结果发表在《科学》杂志上.除了实验上的不断探寻，这些年来理论上的讨论更是给磁单极子予以浓重的理论物理色彩.在电磁学和电动力学课上若希望对磁单极子的讨论予以介绍，通常无法回避其复杂的理论物理基础与背景，导致学生听不懂或理解不了.本文及后继三篇文章尝试克服这个困难，不用过多的理论物理知识，仅在电磁学和电动力学框架内分别介绍磁单极的若干奇特性质，或者说在麦克斯韦方程的框架内有效地实现理论物理对磁单极的各种畅想.由于尽量避免了艰深繁杂的非电磁学理论物理细节，这样给出的磁单极性质描写相比原来的理论物理描述往往图像更加清晰，并容易为学习电磁学和电动力学尚未有足够理论物理基础和背景的普通大学生所理解，而笔者也借助电磁场来体验和展示了理论物理学家的那些荒诞和古灵精怪的奇思妙想.由于在电磁学和电动力学课程中绝大多数讨论的内容是已经发现很久的各种物理现象，把磁单极这样一种在经典电磁现象中唯一尚未被发现的物质新的基本组分的介绍引进电磁学和电动力学课，对提升课程的先进性和趣味也许会有帮助.遗憾的是，关于磁单极的理论讨论通常是十分散乱和零碎的.有鉴于此，笔者分四篇文章分别选四个相互独立的涉及磁单极的例子，依据电磁学和电动力学针对磁单极的特定性质进行详细的介绍和演绎，展示有别于通常理论物理讨论的磁单极子的另类推导.这四篇文章可以看作在前期《物理与工程》杂志上业已发表的《电磁学与电动力学中的超导》文章（2013.23（5））的后继文章，它们的主要内容曾由笔者于2013年7月在云南昆明由国家自然科学基金委员会资助、教育部高等学校物理学类专业教学指导分委员会主办，云南大学物理科学技术学院承办的“2013年全国高等学校电磁学与电动力学课程骨干教师培训班”上进行过讲解和介绍.

2 磁单极与点电荷体系的电磁场角动量

本文讨论涉及磁单极的电磁场的角动量.由于电磁场的角动量要求同时存在磁场和电场时才可能具有，因此考虑一个最基本的满足这样要求的体系，它由一个磁荷为g的磁单极和一个电荷为e的点电荷构成.把磁单极放在坐标原点.这个体系的安排如图1所示，其中磁单极到场点P的矢量为r，点电荷到场点P的矢量为r′，磁单极到点电荷的矢量为R＝r－r′.为方便讨论，进一步引入r方向的单位矢量和r′方向的单位矢量.磁单极在场点P产生的磁场强度H 通过适当的单位制选择可以写为：；点电荷e在场点P产生的电场强度E可以写为：E＝下面先计算这样一个体系的电磁场的总角动量，它可按照标准的电动力学公式写为

图 1

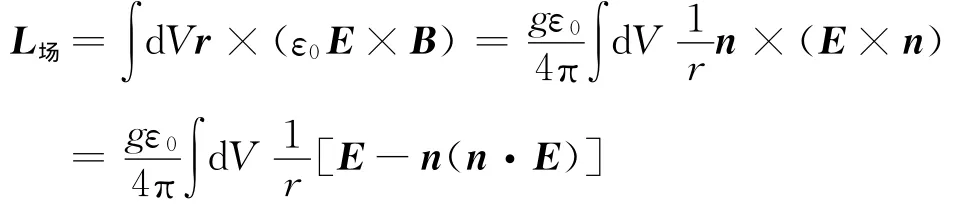
其中，先把磁感应强度B＝μ0H的表达式代入上式并将r改用单位矢量n表达，进一步把叉乘运算改用点乘运算表达.上面结果可以进一步被化简为

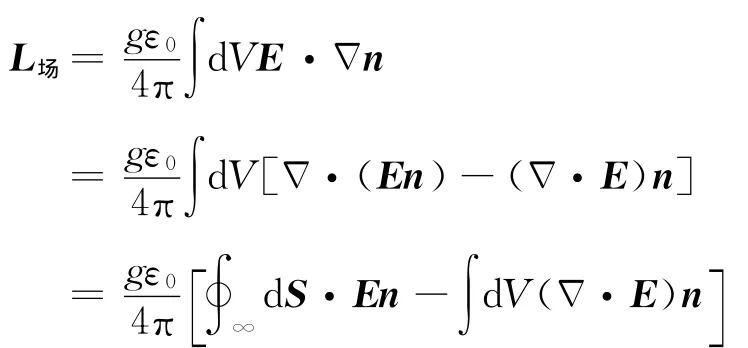
式中，第二个等号内的第一个微商对其后面E的作用所导致的项与第二项正好抵消，剩下第一个微商对其后面n的作用所导致的项正是第一个等号后面所给出的项.在第三个等号后，利用数学上全散度体积分与面积分的互换公式把第二个等式的第一项换为在无穷大空间边界上的面积分，也就是第三个等式的第一项.在这个无穷大的面上，由于距磁单极和点电荷已经是无穷远的距离，n′、r′和n、r之间的差别已经可以忽略，因此电场表达式中的n′和r′完全可以用n 和r来替代，即dΩ，其中，dΩ 是无穷远表面上的无穷小面元对坐标原点张开的无穷小立体角角元.把这个结果用于计算上面公式第三个等式中的第一项＝0，其中，最后的零是因为在4π立体角积分的过程中单位矢量n和它的反向矢量－n总会相互严格抵消掉.对上面公式第三个等式中的第二项中的Δ·E项可以利用麦克斯韦方程组将其化为：

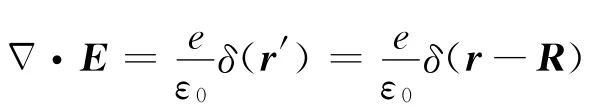
其中，eδ（r′）是点电荷e的电荷密度.利用δ函数可以完成上面公式第三个等式中的第二项中的体积积分，得到结果：

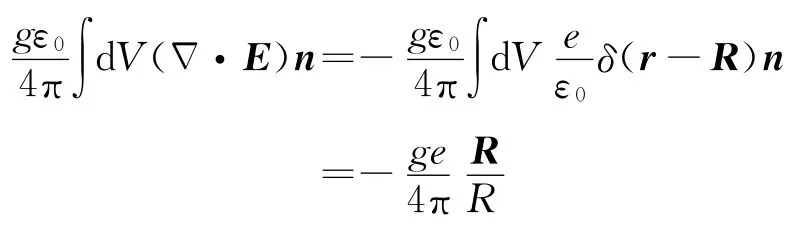
结合前面讨论上述公式第三个等式中的第一项的零结果，最后得到这个由磁单极和点电荷组成的体系的电磁场的总角动量为这是一个极其简单的结果：电磁场总角动量的方向沿点电荷和磁单极的连线方向，大小只依赖于磁单极的磁荷量和点电荷的电量的乘积.虽然这样一个体系的电磁场分布在全空间，因而场的角动量也弥散分布在全空间各处，但所有电磁场的角动量之和确只依赖磁荷和电荷的大小及两者的连线方向.

以上结果的一个更加深刻的引申讨论是：如果考虑到在微观尺度角动量是量子化的（这点是本文唯一超出经典电磁学和电动力学的地方），即角动量的大小不能取连续值，而只能取某个基本单位的整数倍.那么利用刚得到的角动量的大小和磁荷与电荷的简单关系，磁荷与电荷的乘积也不能取连续值，而只能是某个基本值的整数倍.对给定的磁荷，它要求电荷必须是量子化的（即电荷必须取分立值，且是基本单位的整数倍）；反之对给定的电荷，磁荷也必须是量子化的.由于基本的磁单极尚未被发现，因此这个量子化关系尚未能够实际实现，但一旦人类真正找到了（哪怕只有一个）磁单极，上面讨论的量子化条件针对电荷就变成是现实的了.在物理学里，量子化是非常奇妙而又令人匪夷所思的现象，直到今天大部分的量子化问题，我们知道该怎么做，但无法理解为什么要这么做.现在通过这个由磁单极和点电荷组成的体系的电磁场角动量与磁荷和电荷的简洁关系，把两种看起来完全互没关系且很难理解的量子化现象关联起来了：只要存在磁单极，角动量量子化意味着电荷量子化，反过来承认电荷量子化则意味着场的角动量必须量子化（当然我们会问这只导致场角动量的量子化，那么对通常力学里说的机械角动量也许还是没有影响.下面将要通过角动量的转化与守恒说明场角动量的变化可以导致机械角动量的相应变化，由此，场角动量的量子化也就传递到了机械角动量的量子化上）.经典电磁学和电动力学通过这样一个简单的体系展示出其远超越本身的更深层次的物理关系.

3 磁单极与点电荷体系角动量的转化与守恒

由于角动量在力学中经常被作为守恒量来进行讨论和应用，因此自然地会去问对目前这个体系角动量是否也是守恒的.本文的以下部分就详细地讨论这个问题.实际上，从麦克斯韦方程出发可以分别推导出能量、动量和角动量的转化和守恒定律.只不过在通常的电动力学课程教学过程中，大多只讲能量转化和守恒定律，至多再讲一下动量的转化和守恒定律，为了节省课时一般都不会再去涉及角动量的转化和守恒定律.但是考虑到角动量在量子物理中所起的重要作用，如果有可能对角动量的转化和守恒定律是应该设法予以讨论的.著名物理学家费曼就在他的《费曼物理学》的第二册通过一个佯谬例子来说明电磁场的角动量是如何与机械角动量实现相互转化的.对具有角动量的磁单极与点电荷体系，可以通过明显的计算来讨论其可能的角动量的转化与守恒.

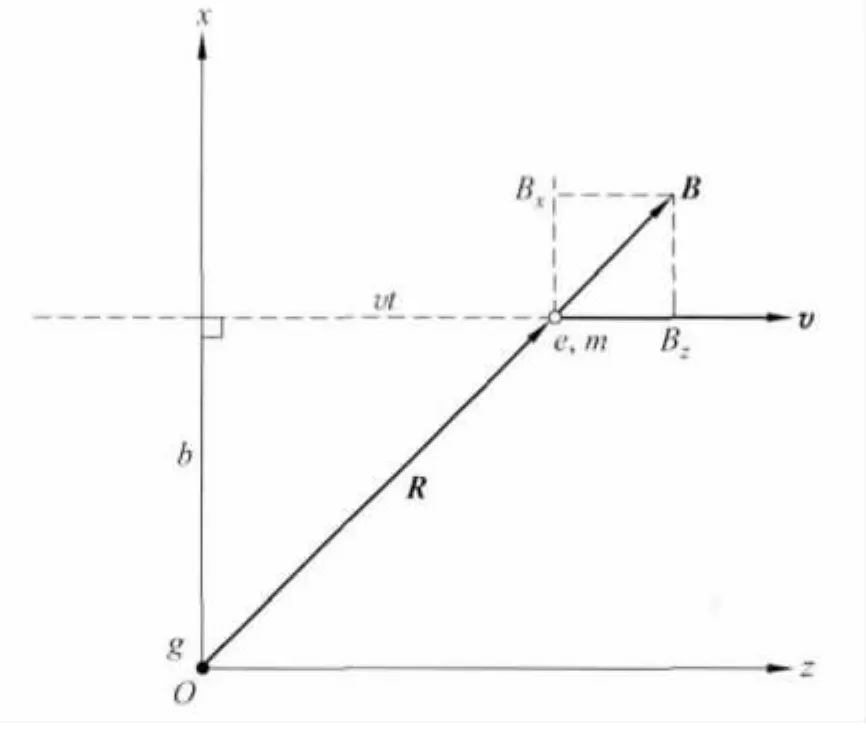
图 2

注意到前面在计算磁单极与点电荷体系中电磁场的角动量时，并未限制电荷与磁单极之间的距离一定是固定不变的，那时的计算只关心在某个时刻点电荷相对磁单极的瞬时位置.由此，可以应用那里的结果到点电荷相对磁单极有相对运动的情形.取磁单极为静止的参考系并把磁单极放在坐标原点，设点电荷相对磁单极的运动速度为，如图2所示.在通常的电磁学或电动力学教材中，有时会看到类似系统被作为例题来进行讨论.的洛伦兹力：.当点电荷从距磁单极位移R运动到位移R＋dR处时，设点电荷的机械角动量的变化为dL机械，则按照角动量的定义：dL机械＝d（R×p）＝（dR）×p＋R×dp＝R×Fdt，其中对第二个等号的第一项利用p＝，发现它实际没有贡献，即（dR）×p＝这样的例题一般是计算一个磁单极从无穷远射向一个带电的点电荷（例如原子核），经过与该点电荷进行弹性散射后飞向无穷远，然后证明在瞄准距离（图2中的参数b）很大时整个过程前后的角动量守恒.在这个例题中讨论的是整体的体系角动量守恒，而目前的例子针对的是局域的角动量的转化和守恒.或换句话说，我们关心具体到某个时刻和相邻的下个时刻时体系的角动量的相互关系，并且对点电荷和磁单极之间的关系不做任何限制.从局域的角动量转化和守恒很容易导出整体的角动量守恒，而反过来则一般无法导出.因此本文选择的讨论比通常教科书中的讨论要更加详细和一般.

对这个相互之间有运动的体系的电磁场总角动量，利用本文前面的计算，已经知道了其电磁场的角动量L场，但这个体系不仅具有电磁场的角动量，如果点电荷具有质量m，则它由于运动还会带有机械角动量L机械.磁单极在目前所选择的参考系下，由于静止在坐标原点，不具有机械角动量.为了讨论角动量的转化和守恒，必须要知道体系的机械角动量L机械.为此先计算一下点电荷受到dR×m＝0，因此dL的计算中只剩下第二个机械等式中的第二项.再利用牛顿第二定律F＝把动量的无穷小变化改用力替代，就得到了第三个等式的结果.进一步代入前面计算的洛伦兹力的结果，发现：

一个磁单极和一个点电荷体系的角动量及其守恒问题很容易被推广到一个磁单极和一团电荷分布的体系.这时只要将整个的电荷分布化为一个个近似可用点电荷代替的小块电荷区域，分别计算其与磁单极之间的角动量，再利用叠加原理把结果叠加起来即可.更复杂地，一团磁荷体系（这时不一定再局限于是磁单极，可以是有效磁荷）和一团电荷体系的角动量及其守恒问题也可以本文的结果为基础通过叠加原理计算出来.从这个角度上，本文给出的是一般的电磁体系的角动量及其守恒问题最基础的讨论.

［1］ 王青.电磁学与电动力学中的超导［J］.物理与工程，2013，23（5）：1－4，9.