换流变压器出线套管极性反转电场计算分析

万 琳，李 琳，刘 刚，孙优良，李文平

1.华北电力大学 新能源电力系统国家重点实验室，北京102206 2.天威保变电气股份有限公司，河北 保定071051

0 引 言

直流输电是目前解决高电压、大容量、远距离送电和电网互联的一个重要手段。直流输电系统中一次设备故障是引起直流系统强迫停运的首要因素，其中，以换流变压器故障引起的直流系统被迫停运次数最多。换流变压器阀侧套管作为换流变压器的外部连接装置，与换流阀阀桥直接相连，是换流变压器最主要的组成部件之一。与普通电力变压器不同，换流变压器阀侧绝缘在运行中要长期承受高幅值的直流和交流工作电压以及各种过电压，还要承受启动、停运和极性反转等动态直流电压。由于静态和动态直流电场的分布都与电阻率密切相关，因电阻率受温度、杂质、原材料和作用场强等因素影响而在很大范围内变化，使直流绝缘的设计存在很大的不确定性，故直流绝缘设计的安全系数取值必须大大高于交流设计的取值。因而换流变压器阀侧出线装置的设计制造比交流出线装置要复杂和困难得多。出线装置绝缘技术被视为换流变压器核心技术而严格保密，其关键技术一直被国外厂家掌握，产品严重依赖进口，该项技术已成为发展我国直流输电设备的瓶颈。随着我国直流输电工程的大规模建设，研发高压和特高压换流变压器出线装置绝缘技术已刻不容缓。

现有文献对换流变压器绝缘结构中的电场分析做了很多研究，文献［1 ～3］分别用有限差分法和有限元方法对换流变压器各向异性非线性媒质中的直流稳态电场进行了研究。文献［4，5］通过数值方法模拟了一台实际的换流变压器极性反转试验中瞬态电场的变化过程。但目前针对出线套管模型的研究还较少，而且在计算过程中进行了大量的简化，往往假设极性反转瞬间完成或只考虑线性媒质条件下的极性反转过程［6～9］。本文利用罚函数法构造出有限元状态方程，利用C-N 法进行求解，完整的模拟了一台±800 kV 换流变压器出线套管在极性反转试验中瞬态电场的变化过程，且通过对线性媒质和非线性媒质条件下的计算结果进行对比分析，考察了非线性对换流变压器出线套管极性反转电场分布的影响。

1 有限元状态方程

换流变压器出线套管中的极性反转电场属于电准静态场，在电准静态场条件下，有损媒质中的电位满足如下初边值问题:

式中:Γ1，Γ2分别为第一类、第二类边界条件。我们首先将计算区域Ω 进行有限元剖分，应用加权余量法，可以得到以节点电位为待求量的半离散方程:

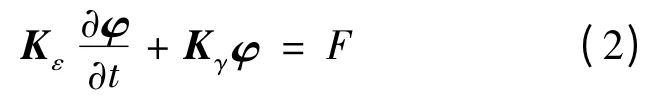
式中:φ 为待求节点电位列向量;F 为含有第二类边界条件的右端项;Kε，Kγ分别为对应于媒质介电常数ε 与电导率γ的有限元系数矩阵。

利用罚函数法施加第一类边界条件后，可得:

或

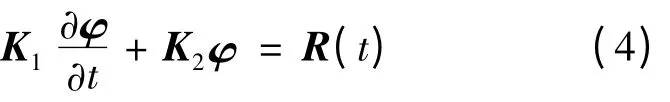
式中:φb为边界节点电位向量;C 是罚系数对角矩阵。

进一步可得到状态方程:

本文考虑了媒质电导率随电场强度变化的非线性问题，未考虑温度和湿度对媒质电导率的影响。这时，媒质的电导率是关于电位分布的函数，即γ = γ(φ)。非线性媒质的有限元状态方程变为

2 C－N 法求解有限元状态方程

求解方程(5)和(6)的数值方法有很多，如模态法、直接积分法、状态空间法及龙格库塔法等。模态法需要计算模态矩阵，在有限元分析中，矩阵K1和K2都是稀疏矩阵而模态矩阵是满阵，利用模态法求解是不保稀疏的，所以不宜采用本方法进行分析;状态空间法是一种直接泰勒级数展开方法，由于在非线性问题中，阻性系数矩阵K2是关于电位φ 的函数，使得利用泰勒级数展开方法变得极为困难;龙格库塔法既可以用来求解线性媒质问题，也可以用来求解非线性媒质问题，但在求解非线性媒质问题时，由于阻性系数矩阵K2是关于电位φ 的函数，所以每求一次都要根据电位分布φ 来重新生成一次阻性系数矩阵，计算代价较高;C-N 法具有二阶精度，对于非线性不是很强的问题，它在每时步的计算量较少，因此在满足工程精度的前提下可以大大减少计算量。本文综合考虑了计算精度和速度两个方面，选择利用C-N 法来获得此状态方程的数值解。

将(4)式时间离散化，可得到如下全离散格式:

式中:n，n +1 为计算的时间步;a 为系数，当a 的值为0，1 和0.5 时，分别对应于向前欧拉法、向后欧拉法和C-N(Crank-Nicolson)法。其中后向欧拉法和C-N 法是无条件稳定的，但后向欧拉法只有一阶精度，而C-N 法具有二阶精度，因此在电气工程领域中常常被采用。

考虑电导率－电场强度非线性时，式(7)中Kγ为电场强度φ 的函数，为简化公式，本文用Kγ(φ)表示Kγ(－ ▽φ)。此时C-N 的公式变成如式(8)形式:

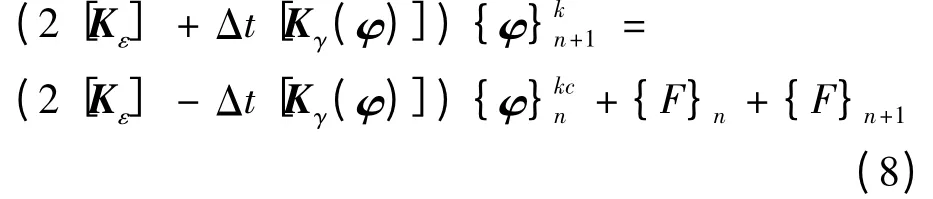
式中:k，kc 分别表示n+1 时刻的迭代次数和n 时刻迭代收敛时的迭代次数。

3 换流变压器出线套管极性反转试验数值模拟

3.1 极性反转电压

完整的极性反转试验需要进行两次反转过程，电压波形如图1 所示，具体变化过程如下:

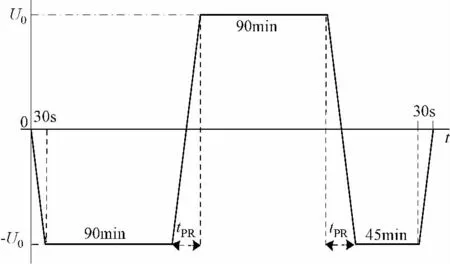
图1 极性反转电压波形Fig.1 Curve of polarity reversal voltage

a.在30 s 内由0 电位降到－U0，保持90 min;

b.在一定时间tPR内由－U0上升到+U0，并保持90 min;

c.在一定时间tPR内由+U0下降到－U0，并保持45 min;

d.在30 s 内均匀变化到0。

IEC 推荐两次极性反转过程不超过2 min，一般取1 min。本文计算时取为tPR=1 min。

3.2 非线性参数选取

本文在进行非线性分析时，采用指数函数重新拟合了图2 中油的电场强度－电导率非线性曲线，函数关系式见式(9)和式(10):

式中:E 为电场强度，kV/mm;γ0paper和γ0oil是室温条件下，E=0 时的电导率估算值;γpaper和γoil分别是绝缘纸板和变压器油的电导率，S/m。取β =0.017，N=7，系数ai(i=1，2，…，7)值根据图2 的电导率－电场强度曲线拟合得到，具体值见表1。

图2 电场强度－电导率非线性曲线Fig.2 Nonlinear curves of electric field dependent conductivity of transformer oil and oil-immersed paper

表1 油非线性系数Tab.1 Nonlinear Coefficients for transformer oil kV/mm

3.3 极性反转试验的数值模拟

本文的计算模型是一个实际±800 kV 换流变压器出线套管绝缘结构模型，如图3 所示，极性反转电压为970 kV。将出线套管模型进行有限元剖分，剖分得到186 616 个三角形单元，93 493 个节点，剖分结果如图4 所示。

三角形内电位采用线性插值，线性/非线性媒质时的极性反转瞬态过程用C-N 法分析，步长为30 s。对瞬态法得到的节点电位结果进行处理，可以分别得到第一次反转前(89.5 min)后(90.5min)和第二次反转前(179.5 min)后(180.5 min)各种媒质中的最大电场强度见表2 ～3。表2 和表3 中89.5，90.5，179.5，180.5 所在行的值表示相应时刻各种媒质中的最大电场强度值。

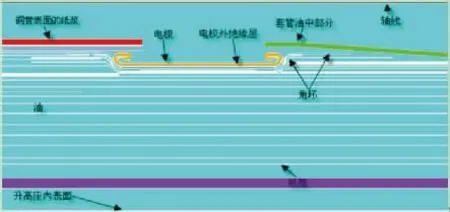
图3 出线套管实际模型Fig.3 The model of out-let bushing

图4 套管剖分图Fig.4 The dissect picture of bushing

表2 非线性媒质时的最大电场强度Tab.2 Maximum electric fields in linear materials V/m×107

表3 非线性媒质时的最大电场强度Tab.3 Maximum electric fields in nonlinear materials V/m×107

通过表2、表3 可以看出，不论是在线性还是非线性媒质条件下，油中最大电场强度值在两次反转前后发生剧变，数值均大大增加。

通过表2、表3 的对比可以发现，与线性直流电场相比，非线性直流电场时绝缘纸板、变压器油中的最高场强值均变小，绝缘纸板中由1.203 9减至0.802 0，变压器油中由1.437 9 减至0.733 5;这是由于非线性时，油纸的电导率均增加，油纸界面电荷在1 min 的反转时间内消散较多，从而导致反转完成瞬间的电荷电场与反转前大不相同，而线性条件下由于1 min 内空间电荷消散的量很少，因此会出现斜坡电压下线性/非线性结果的巨大差异。因此，不考虑材料非线性特征时计算结果常趋于保守，增大了绝缘难度。

为了考察电场强度的瞬变特性，本文在油、纸筒、绝缘层、瓷套4 种媒质中选取了4 个单元给出了这4 个单元电场强度随时间变化曲线(图5，6)。

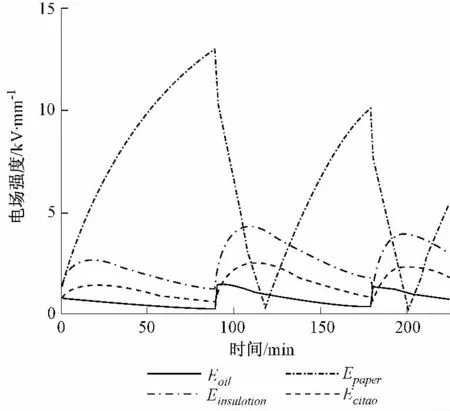
图5 线性媒质时的电场强度变化曲线Fig.5 Electric field curves in linear materials

图6 非线性媒质时的电场强度变化曲线Fig.6 Electric field curves in nonlinear materials

由以上2 图可以看出，电导率最大的材料(油)最大场强出现在极性反转瞬间，电导率最小的材料(纸筒)最大场强出现在趋近稳态时，其他材料则是发生在极性反转过程中。绝缘纸筒中电场强度较大，而油中的电场强度较小，因为反转电压作用下的阻性电场集中分布在电阻率较高的绝缘纸中。而在极性反转的1 min 内，变压器油的电场强度在不断增加，而油浸纸和绝缘纸的电场强度却在不断减小，这是因为激励电压由一种稳态变化到另一种稳态时，电场中产生一个瞬变过程。

但我们也可以明显的看出虽然每次反转发生时，各媒质中的电场强度仍处于上升或下降状态，但非线性条件下的各媒质中电场强度更趋于稳态，并且非线性条件下，反转完成后，绝缘层和油浸纸板到达其最小电场强所需时间明显缩短，这是由于电导率的非线性引起的。

下面给出极性反转过程中不同时刻的电位分布云图，V;如图7 ～10。

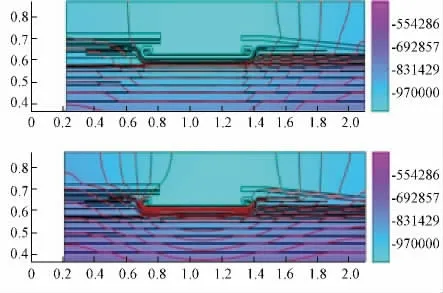
图7 89.5 min 时刻( 第一次反转前) 线性/非线性媒质时的电位分布Fig.7 Potential distributions in linear/nonlinear materials at 89.5 min

图8 90.5 min 时刻( 第一次反转后) 线性/非线性媒质时的电位分布Fig.8 Potential distributions in linear/nonlinear materials at 90.5 min

图9 179.5 min 时刻( 第二次反转前) 线性/非线性媒质时的电位分布Fig.9 Potential distributions in linear/nonlinear materials at 179.5 min

图10 180.5 min 时刻( 第二次反转后) 线性/非线性媒质时的电位分布Fig.10 Potential distributions in linear/nonlinear materials at 180.5 min

从以图7 ～10 可以看出，极性反转后瞬间等位线的形状发生扭转和回环，甚至出现了局部等位线闭合的情况，此种情况说明在电压极性反转过程中，在绝缘介质的交界面上出现了孤立的空间电荷，而且此种电荷的分布比较复杂，大量的空间电荷造成了局部电位的升高或降低而形成“电位高峰”或“电位低谷”，并进一步形成了空间电荷间的附加电场，此附加电场叠加到原电场上引起了电场的畸变，即等位线的扭曲和回环。由此可见，空间电荷对极性反转后瞬间的电场分布产生实质作用。

对比线性和非线性情况，考虑材料的非线性时，油纸交界面，尤其在一些拐角、折角处，等位线分布较线性电场均匀。

在考虑到短时极性反转过程时，非线性的计算结果要比相应的线性结果小50 %，这对绝缘设计是很有意义的。实际绝缘计算中，绝缘材料电阻率取为常数，但这种条件下的计算结果可能与实际反转电场分布有很大的不同。因而要进行实际换流变压器出线套管极性反转电场的数值模拟，很有必要开展电导率—电场强度、电导率—温度等基础参数的测量工作，并将实测参数用于换流变压器出线套管极性反转电场的数值计算。

4 结 论

本文应用有限元法，仿真计算了在极性反转试验中±800 kV 换流变压器出线套管的电位和电场分布，并对线性和非线性条件下的计算结果进行对比分析，得出:

(1)±800 kV 换流变压器出线套管线性/非线性媒质条件下的极性反转过程结果表明，非线性条件下的电场分布明显不同于线性条件下的结果，在不考虑材料非线性特征时计算结果常趋于保守，大大增加了绝缘设计的难度。

(2)在考虑到短时极性反转过程时，非线性的计算结果要比相应的线性结果小50 %。

(3)油中最大电场强度值在反转前后发生剧变，最大电场强度值在反转过程中大大增加，反转完成后电场强度值又迅速减小。

(4)电导率最大的材料(油)最大场强出现在极性反转完成时刻，电导率最小的材料(纸筒)最大场强出现在趋近稳态时，其他材料则是发生在极性反转过程中。

(5)空间电荷会对极性反转后瞬间的电场分布产生实质作用。

［1］Takahashi E，Shirasaka Y，Okuyama K.Analysis of anisotropic nonlinear electric field with a discussion of dielectric tests for converter transformers and smoothing reactors ［J］.IEEE Transactions on Power Delivery，1994，9 (3):1480 －1486.

［2］吕晓德，陈世坤，孙定华，等.各向异性非线性直流电场数值算法研究［J］.电工技术学报，1998，13 (4):60 －64.

［3］Li Jinbiao，Xie Dexin，Wang Xiaoyan.Adaptive FE analysis of nonlinear and anisotropic DC electric field of converter transformer in HVDC transmission systems［C］ //Automation Congress，2008.WAC 2008.World.Hawaii，HI:IEEE，2008:1 －4.

［4］李琳，纪锋，刘刚.油纸绝缘结构瞬态电场计算的状态空间有限元法［J］.中国电机工程学报，2010，30 (36):111 －116.

［5］李琳，纪锋，李文平，等.换流变压器极性反转试验的数值模拟［J］.中 国电机工程学报，2011，31(18):107 －112.

［6］张学成，檀金华，牛万宇，等.1 100 kV 直流输电工程换流变压器阀侧套管的设计［J］.高电压技术，2012，38 (2):393－399.

［7］郑劲，文闿成.换流变压器阀侧套管出线装置绝缘分析［J］.高电压技术，2010，36 (5):1184 －1190.

［8］张喜乐，王建民，吴增泊，等.超高压直流换流变压器阀侧引出线电场的数值分析［J］.变压器，2009，46 (7):1 －10.

［9］刘鹏，彭宗仁，党镇平，等.极性反转试验中+800kV 换流变压器套管尾部的电场分布研究［J］.电磁避雷器，2009 (3):1 －4，8.

［10］Wen K C，Zhou Y B，Fu J，et al.A calculation method and some features of transient field under polarity reversal voltage in HVDC insulation ［J］.IEEE Transactions on Power Delivery，1993，8 (1):223 －230.

［11］张艳丽，谢德馨.换流变压器内部暂态电场分析［J］.沈阳工业大学学报，2001，23 (6):467 －470.

［12］陈健，李建柱.换流变压器在极性反转下的瞬态电场分布特性研究［J］.研究与分析，2011，，11(05):28 －30.

［13］李季，罗隆福，许加柱，等.换流变压器阀侧绝缘电场特性研究［J］.高电压技术，2006，32 (9):121 －124.

［14］李文平，章忠国，黎小林，等.直流输电用800 kV换流变压器的场域分析［J］.变压器，2009，46(6):l－5.

［15］盛剑霓.工程电磁场数值分析［M］西安:西安交通大学出版社，1991.

［16］赵畹君.高压直流输电工程技术［J］.北京:中国电力出版社，2004.

［17］蒋蓁.换流变压器出线装置的绝缘结构分析［J］.高压电器，2011，47 (3):69 －71.