基于最小二乘支持向量机的锅炉对流受热面清洁吸热量预测

安连锁，马美倩，沈国清，张世平，吕伟为

(华北电力大学 电站设备状态监测与控制教育部重点实验室，北京102206)

0 引 言

当电站锅炉受热面污染 (积灰和结渣)时，比较明显的表现形式是受热面的换热能力变差，对于锅炉对流受热面来说，主要体现在受热面的吸热量减少，基于此，目前电站锅炉对流受热面污染监测广泛采用清洁因子法，即用受热面实际吸热量与受热面清洁时的潜在吸热量的比值定义清洁因子，与临界清洁因子对比判断受热面污染状况。受热面实际吸热量可以通过电厂数据采集系统 (DAS)实时采集的工质侧各参数、锅炉计算燃料量等计算获得，清洁时潜在吸热量则需要采用一定的辅助手段进行预测，因此准确地获得电站锅炉对流受热面清洁时潜在吸热量，是对流受热面污染监测的重要环节。

目前，对于对流受热面清洁时潜在吸热量的预测大多采用神经网络法，文献［1 ～3］ 建立了对流受热面清洁时潜在吸热量预测神经网络模型。但神经网络要求多样本，采用小样本时容易出现过度训练，而实际情况下在电厂获得的样本数量往往是有限的，此外神经网络拓扑结构复杂，最终获得的仅仅为局部最优解，这些问题使神经网络一定程度上限制了该吸热量预测的准确性。

本文提出基于最小二乘支持向量机 (LSSVM)的锅炉对流受热面清洁时潜在吸热量预测模型，采集相关数据对模型的可行性进行了验证分析，同时建立神经网络模型进行对比分析，结果表明最小二乘支持向量机预测模型可以克服神经网络预测模型的缺点，预测精度高，使用该预测模型将使对流受热面污染监测更为准确。

1 最小二乘支持向量机

支持向量机 (SVM)是在统计学习理论的结构风险最小化和VC 维理论下产生出来的一种新的通用机器学习方法，适合小样本，能够自动地获得网络拓扑结构，泛化能力强，其理论上为凸优化问题，获得的是全局的最优解，解决了神经网络法的局部最优问题，最小二乘支持向量机(LS-SVM)是在支持向量机基础上提出来的，它将支持向量机的不等式约束问题转化为等式约束问题，也即将求解的二次规划问题转化为一组等式方程求解问题，需确定的参数变少，求解速度较普通的支持向量机 (SVM)速度变快，其已经成功地应用到降雨量、时用水量、数控机床热误差等预测中［4～6］。

LS-SVM 算法的推导过程如下:

对于待回归的非线性数据集T，假设T ={(x1，y1)，(x2，y2)，…，(xi，yi)，… ，(xm，ym)}，且其中xi，yi∈R，如果假定存在函数f(x)= ω·x + b 在精度ε 下能够估计所有的(xi，yi)数据，引入松弛变量ξξ*，则对SVM 来说，寻找最小ω 的问题可以表示成如下凸优化问题:

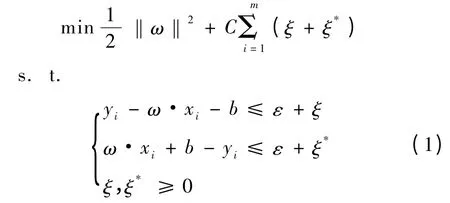
其中，ε 为不敏感损失函数，C ＞0。

LS-SVM 相比基本的SVM 回归模型减少了不敏感损失函数ε 这一参数，约束条件转化为等式约束，式 (1)的优化问题转化为

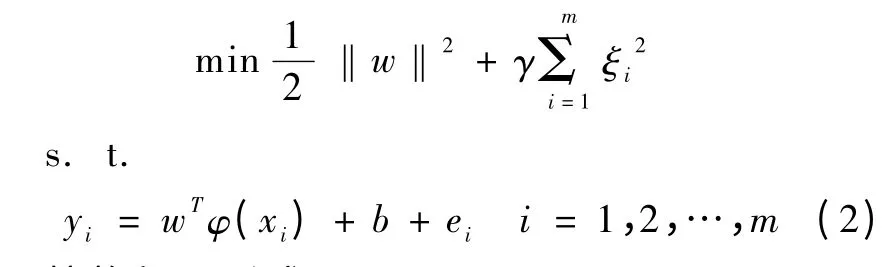
拉格朗日形式:

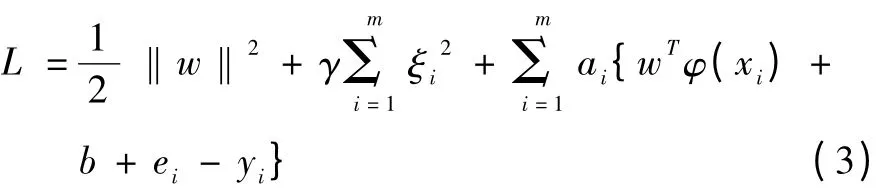
根据KKT 条件:

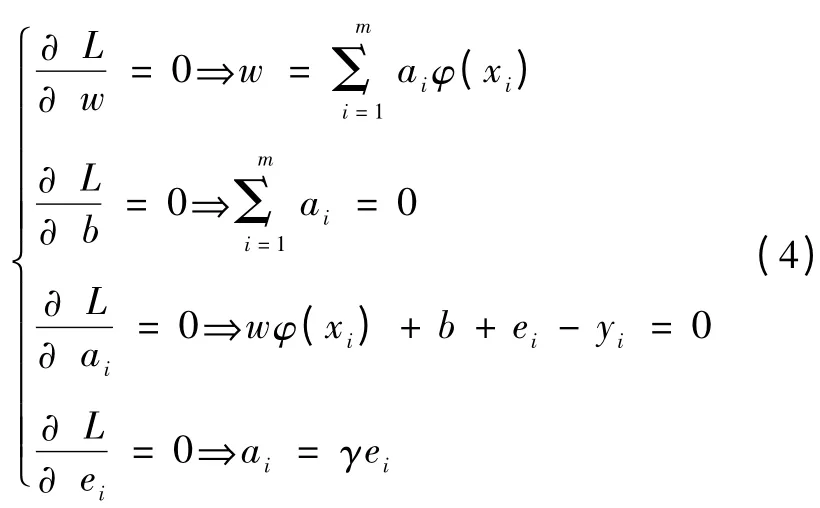
消去ei，w，求解可以得到回归函数:

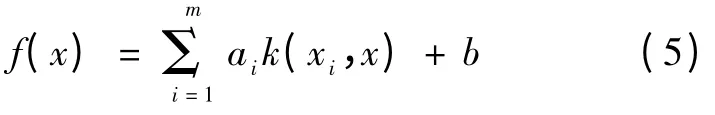
由上述推导过程可以看出，相比于基本的SVM 回归模型，LS-SVM 采用等式约束，简化了算法的复杂性，提高了预测模型的收敛速度，计算过程中减少了不敏感损失函数ε 的确定，只需要确定核函数k(xi，x)的宽度σ 和调整参数γ，模型相对更为简单，因此本文选用LS-SVM 作为预测工具［7］。

2 吸热量预测实例分析

本文选择某电厂330 MW 锅炉对流受热面清洁时潜在吸热量作实例的预测分析，该锅炉为亚临界参数自然循环汽包炉，采用四角切圆燃烧方式，使用一次中间再热。锅炉结构如图1所示。

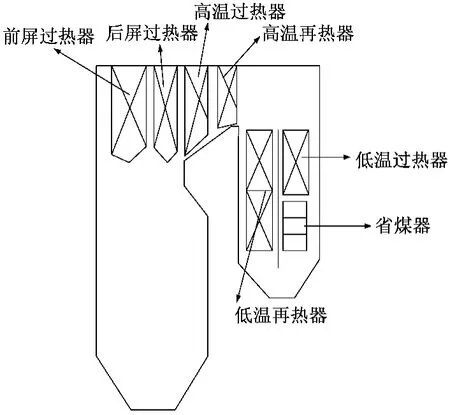
图1 锅炉结构简图Fig.1 Schematic diagram of boiler structure

2.1 输入参数的选择

本文预测对流受热面清洁时潜在吸热量，因此输入参数选择对其影响较大的参数:首先考虑到受热面管内工质的流动状况以及负荷变化对受热面换热的影响，引入管内工质的流量、压力以及进出口温度作为输入参数;其次考虑煤的变化对受热面换热的影响，引入总给煤量;最后，考虑炉内因素，影响受热面吸热量的因素主要是烟气量以及烟气进 (出)口温度，烟气量的大小可以用进风量 (即一次风量、二次风量)大小来反映，对烟气进 (出)口温度，尾部低温受热面(如省煤器)烟温较低，一般布置有烟温测点，可以直接通过测温仪器测量，高温受热面，在锅炉整体热平衡基础上，可以从省煤器的出口开始逆烟气流程根据工质侧和烟气侧的热平衡逐次地计算获得。综上所述，本文预测模型的输入参数主要为:管内工质的流量、压力以及进出口温度;总给煤量;一次风量;二次风量;入口烟温。

2.2 数据的采集

现代电厂数据采集系统 (DAS)完善，拥有大量的测点，可以为操作人员提供压力、温度等各种热工参数。论文所需实验数据就是从电厂的数据采集系统 (DAS)获得的。由于本文采集对流受热面清洁时潜在吸热量预测用数据，因此采集数据的前提应为受热面为清洁状态，但实际情况下，受热面完全清洁的状态是不存在的，所以我们取吹灰停止 (以直接吹扫该受热面的全部吹灰器结束为准)10 分钟后受热面为清洁受热面，从电厂DAS 系统中获取此时受热面的各需求参数存入数据库中，为了能够达到更好地预测效果，采集的数据应包括尽可能多的运行工况下的运行参数。采集的数据分为两部分，一部分用于训练LS-SVM 预测模型，另一部分用于验证已经训练好的预测模型的准确度。

2.3 数据的归一化处理

由于采集的不同输入参数的数据在单位和大小上存在很大差异，因此需要对采集到的数据进行归一化处理，将其转化成无量纲且范围在［0，1］ 的数据，预测后将预测得到的数据进行反归一化即可得到需要的预测数据。常见的归一化处理的式子为

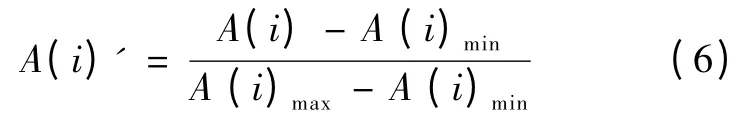
式中:

A(i)为归一前某参数数值;A(i)′为参数归一处理后数据;A (i)min，A (i)max分别为归一前某参数的最小、最大值。

2.4 核函数的选择

由LS-SVM 理论的介绍可知，LS-SVM 是通过核函数来实现非线性函数映射到高维特征空间进而在这个空间内实现线性回归的，因此核函数的选取是构建LS-SVM 预测模型的重要环节。目前，常用的核函数有多项式核函数、sigmoid 核函数以及Gauss 径向基核函数 (RBF)。

多项式核函数:其数学表达式为k(xi，x)=((xi·x)+ c)d，c = 0 时为齐次多项式核，c ＞0时为非齐次多项式核，多项式核函数在应用于维数很高 (即d 值很大时)的特征空间时计算量大，计算精度不高;

sigmoid 核函数:其数学表达式为k(xi，x)=tanh(ν(x·xi)+ c)，其中ν ＞0，c ＜0，此核函数不是正定核，公式中的参数ν、c 只对部分值满足Mercer 条件，因此该核函数的应用存在着一定局限性，但在某些实际应用中却非常有效;

Gauss 径向基核函数:其数学表达式为k(xi，x)= exp(- ‖xi- x‖2/σ2)，是目前普遍采用的一种核函数，它将样本数据的非线性转换到高维空间里，表现形式简单，解析性好，在特定参数选择下线性函数是径向基函数的一个特例;

通过对上述三种常用的核函数的对比研究分析，相同情况取平均误差最小的原则下，本文选择Gauss 径向基函数 (RBF)作为LS-SVM 预测模型的核函数［8，9］。

2.5 预测结果分析

利用上述原理和方法，以锅炉低温过热器为例，本文采用LS-SVM 对其清洁时潜在吸热量进行了预测，建立如下LS-SVM 预测模型:采用Gauss 径向基函数 (RBF)作为核函数，通过参数寻优函数tunelssvm 确定σ2和γ 的取值，经过寻优过程，取模型平均绝对误差最小时，即σ2和γ 分别取值9.4，1782.2 作为模型用参数，采集150 组数据，120 组作为训练集训练模型，30 组作为验证集来验证模型的准确度。最小二乘支持向量机验证集预测效果如图2 所示。

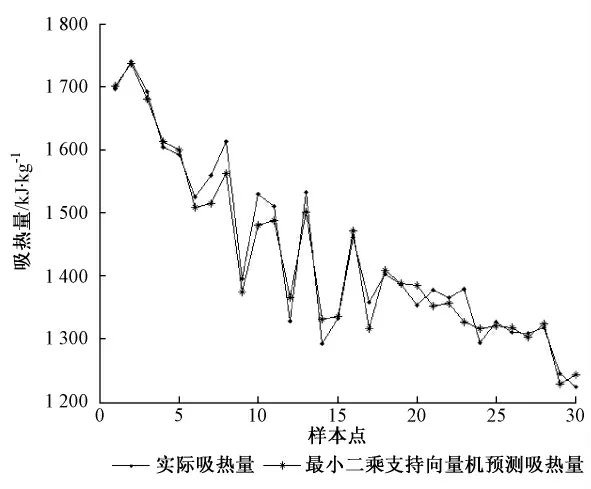
图2 最小二乘支持向量机预测效果图Fig.2 Prediction effects diagram of least squares support vector machines (LS-SVM)

为了验证LS-SVM 预测的准确度，在采用与LS-SVM 相同的输入参数、数据采集和数据处理方式的前提下，本文同时使用目前常用的BP 神经网络做预测进行对比研究，经过模型的训练研究，本文最终采用的BP 神经网络包含三层:输入层、隐含层以及输出层，输入层包含8 个神经元，隐含层包含18 个神经元，输出层包含1 个神经元，隐含层和输出层分别采用sigmoid 函数和purelin 线性函数进行传递，BP 算法采用trainbr 训练函数，神经网络结构、验证集预测效果如图3、4 所示［1～3］:

对流受热面清洁时潜在吸热量实际值、LS-SVM模型和神经网络模型预测值对比结果见表1。

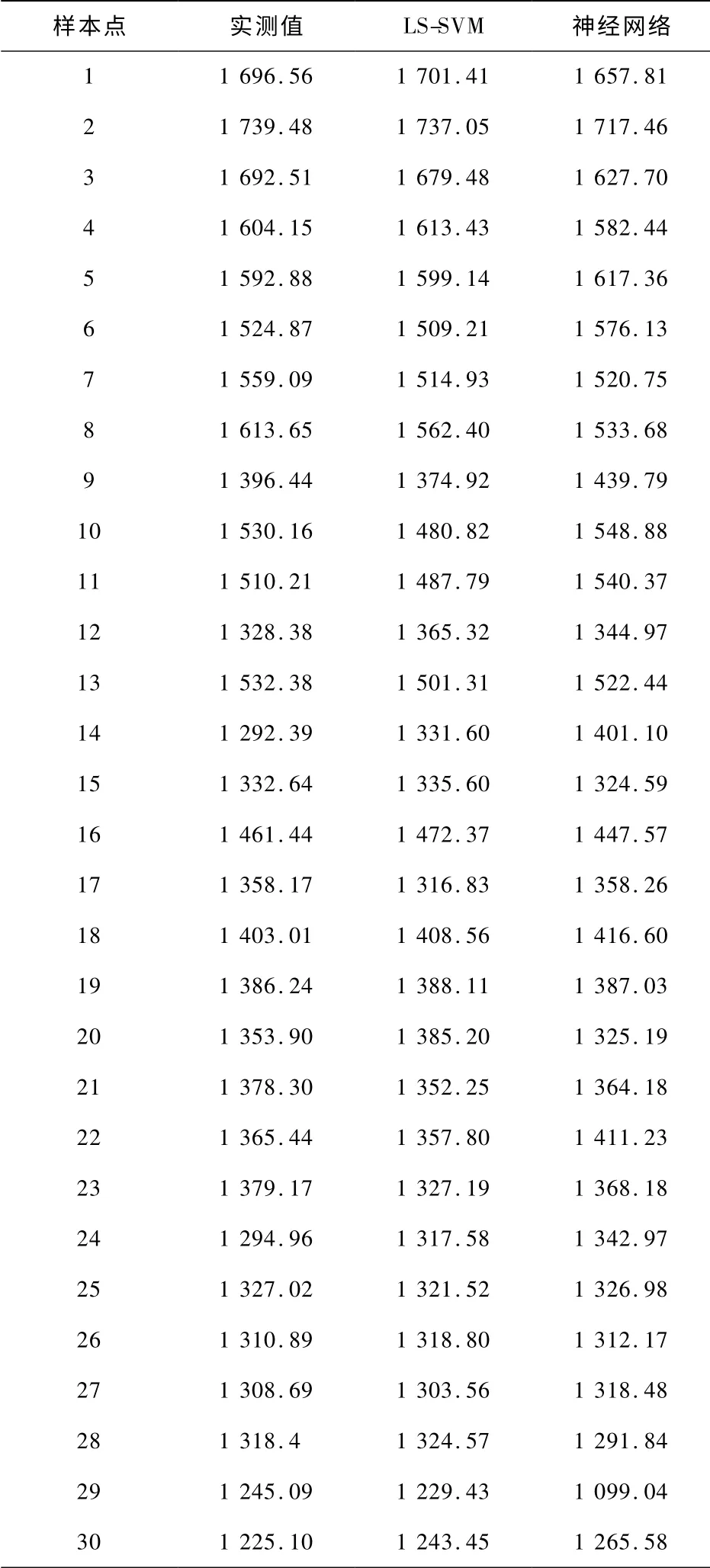
表1 吸热量实际值与预测值对照表Tab.1 Comparison of heat absorption measured values and predicted values (kJ·kg－1)

本文选择相对误差 (RPE )作为实验结果的评价指标。

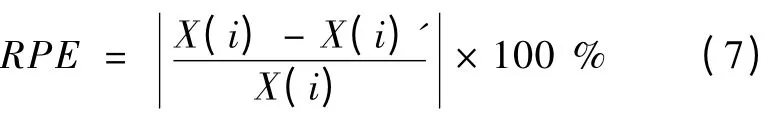
式中:X (i)表示对流受热面实际吸热量，X (i)′表示LS-SVM 或神经网络预测的清洁时潜在吸热量。

本文相对误差 (RPE )对比结果如图5 所示:

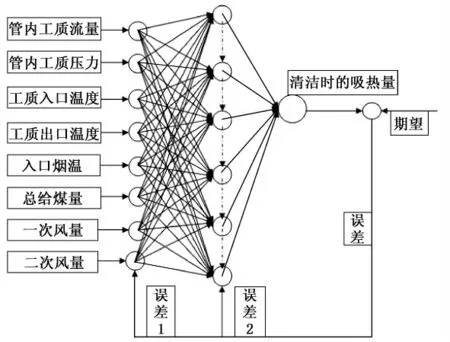
图3 神经网络结构图Fig.3 Structure diagram of neural network

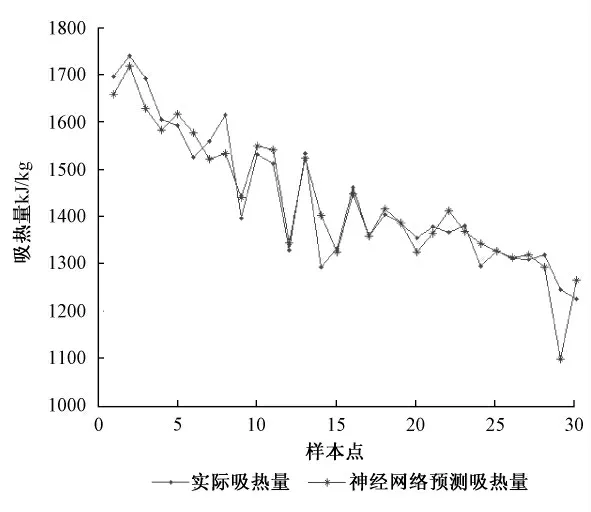
图4 神经网络预测效果图Fig.4 Prediction effects diagram of neural network

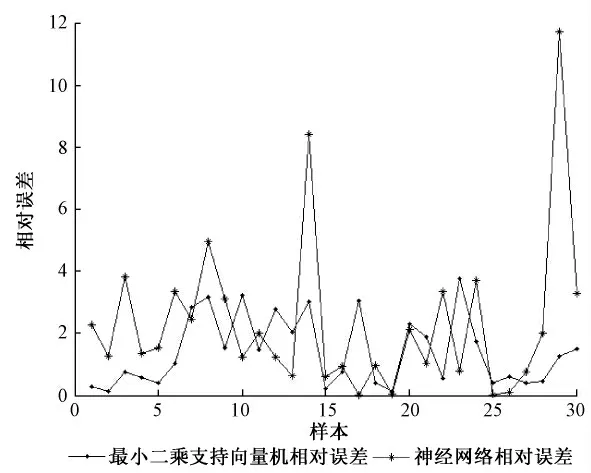
图5 相对误差对比图Fig.5 Comparison diagram of relative error

本文使用平均绝对误差 (MAE)、平均绝对百分误差 (MAPE)以及均方差 (MSE)三个标准作为衡量预测性能的指标，各误差的计算公式如下:

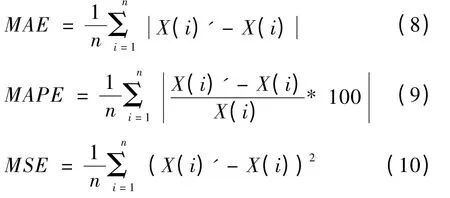
式中:X (i)、X (i)′同上，n 为采样个数。本文两模型各性能对照如表2。

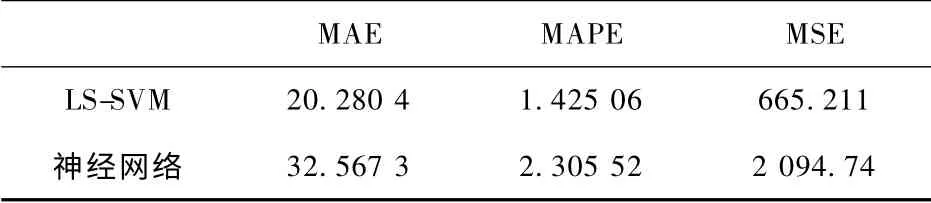
表2 最小二乘支持向量机与神经网络性能对照Tab.2 Comparison of least squares support vector machines(LS-SVM)and neural network

根据以上分析，由图2 LS-SVM 预测效果图、图4 神经网络预测效果图、图5 相对误差对比图以及表二LS-SVM 与神经网络模型性能对照表可知，LS-SVM 较神经网络具有更高的拟合度，各性能都高于神经网络，其验证集预测相对误差控制在4 %以内，而神经网络验证集预测平均相对误差较大，且存在相对误差在5 %以上的点，预测不稳定。神经网络预测误差大的主要原因在于其基于经验风险最小化，容易陷入局部最优和产生过学习问题 (即训练时预测误差变小但验证时预测误差却变大)，LS-SVM 基于结构风险最小化，它综合地考虑置信区间和经验风险，获得的实际风险更小;根据有限样本的信息，在“对特定的样本的学习精度”和“无错误的识别任意样本”之间寻找最好的折衷，因此LS-SVM 预测误差更小，具有更好的预测性能［4，5，6，9］。

3 结 论

本文提出了基于LS-SVM 的电站锅炉对流受热面清洁时潜在吸热量预测方法，建立了LSSVM 预测模型，并与神经网络预测模型进行了对比，结果表明:LS-SVM 预测误差小，预测稳定，各性能高，在对流受热面清洁时潜在吸热量预测方面明显优于神经网络，基于LS-SVM 的锅炉对流受热面清洁时潜在吸热量预测方法具有更好的应用前景，将成为电站锅炉对流受热面清洁时潜在吸热量预测也即电站锅炉对流受热面污染监测方面更为有利的工具。

［1］万俊松，基于人工神经网络和遗传算法的锅炉对流受热面污染监测研究［D］.南京:东南大学，2006.Wan Junsong，Monitoring Ash Fouling onThe Boiler Convection Surfaces Based on The BP Neural Network And Genetic Algorithm ［D］.southeast university.2006.

［2］喻火明，电站锅炉受热面积灰结渣在线监测的研究［D］.北京:华北电力大学，2006.Yu Huoming，A Study on the on_ line Monitoring of Fuling，Slagging of Heating Surfaces of Unility Boiler［D］.Beijing:North China Electric Power University，2006.

［3］吴观辉，向文国.基于神经网络的锅炉对流受热面灰污监测研究［J］.锅炉技术，2005，36 (2):18－20.Wu Guanhui，Xiang Wenguo.Monitoring Ash Fouling onThe Boiler Convection Surfaces Based on The Neural Network ［J］.Boiler Technology，2005，36 (2):18－20.

［4］罗伟，习勇华.基于最小二乘支持向量机的降雨量预测［J］.人民长江，2008，39 (19):29 －31.Luo Wei，Xi Yonghua.Rainfall forecast model based on least squares support vector machine ［J］.Yangtze River.2008，39 (19):29 －31.

［5］陈磊，张土桥.基于最小二乘支持向量机的时用水量预测模型［J］.哈尔滨工业大学学报，2006，389 (9):1528 －1530.Chen Lei，Zhang Tuqiao.Hourly water dem and forecast model based on least squares support vector machine ［J］.Journal of Harbin Institute of Technology.2006，389 (9):1528 －1530.

［6］林伟青，傅建中，许亚洲，等.基于最小二乘支持向量机的数控机床热误差预测［J］.浙江大学学报，2008，42 (6):905 －908.Lin Weiqing，Fu Jianzhong，Xu Yazhou，Chen Zichen.Thermal error prediction of numerical control machine tools based on least squares support vector machine［J］.Journal of Zhejiang University.2008，42 (6):905 －908.

［7］王定成.支持向量机建模预测与控制［M］.北京:气象出版社，2009.Wang Dingcheng.Support Vector Machine Model Prediction and Control ［M］Beijing:Meteorological Press，2009.

［8］邓乃扬，田英杰.数据挖掘的新方法:支持向量机［M］.北京:科学出版社，2004.Deng Naiyang，Tian Yingjie.New Methods of Data Mining:Support Vector Machines ［M］.Beijing:Science Press，2004.

［9］ 杜鹃.基于支持向量机的非线性预测控制研究［D］.杭州:浙江大学，2006.Du Juan， Research onNonlinear Predictive Control Based on Support Vector Machine ［D］.Zhejiang University.2006.