光谱与空间局部相关的SVR影像融合方法
2013-07-25王慧贤江万寿雷呈强张一鸣
王慧贤,江万寿,雷呈强,张一鸣
1.武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079;2.军械工程学院 电子与光学工程系,河北 石家庄 050003;3.北京市遥感信息研究所,北京 100192
1 引 言
随着对地观测技术的发展,大多数对地观测卫星如Landsat-7、Spot 5、IKONOS、QuickBird、GeoEye-1和WorldView-2可以同时提供高光谱分辨率的多光谱影像和高空间分辨率的全色影像。为了充分利用光谱和空间特性,影像融合技术得到了迅速的发展。由文献[1—2]可知,目前的遥感影像融合方法可以分为投影替换类、相对光谱分布类、结构注入空间分辨率增强类ARSIS(amélioration de la résolution spatiale par injection de structures)及混合模型法4类。以IHS(intensity-hue-saturation)[3]、PCA (principle component analysis)[4]、gram-schmidt spectral[5]、HCS(hyperspherical color sharpening)[6]和偏微分替换[7]为代表的投影替换类算法,利用全色波段或其变体替换多光谱影像投影变换后得到的亮度分量,然后进行投影逆变换获得融合结果;以Brovey[8]、合成变量比(synthetic variable ratio,SVR)[9]为代表的相对光谱分布类算法,基于全色影像与多光谱影像之间的线性组合假设,把全色影像信息按比例分布到多光谱影像的各个波段;以 Wavelets[10-11]、Curvelets[12]、HPF(high-pass filtering)[13]、multiscale toggle contrast operator[14]、Markov random field(MRF)models[15]和多尺度光谱增益调制[16]为代表的ARSIS类算法在不同尺度上提取影像的空间信息和光谱信息进行影像融合。投影替换和相对光谱分布这两类算法能够较好地保持空间分辨率,但都依赖于全色影像与多光谱影像的相关性,相关性越好融合结果越好,且光谱信息的保持依赖于传感器的配置和影像信息本身。ARSIS类算法能够较好地保持光谱特性,但是全色影像和多光谱影像空间信息的不一致容易造成空间细节信息的混叠,导致空间分辨率的降低。混合模型算法[17]则试图吸收前3类算法在空间信息保持或光谱信息保持的优势,并引入 Map估计[18]、稀疏表达[19-20]、压缩感知[21-22]等新理论,该类算法研究处于起步阶段,算法也比较复杂,离实用化还有一定距离。
总之,相对光谱分布类的代表性算法SVR算法具有明确的物理意义和理论基础,在全色波段和多光谱波段(或部分波段)能够相互覆盖的条件下(如IKONOS、QuickBird),不仅能保持全色影像的空间细节,也能很好地保持多光谱影像(multispectral image,MS)的光谱信息。然而,对于不满足光谱覆盖条件的影像,SVR会造成融合影像的光谱扭曲[23]。另外,对于满足光谱覆盖条件的影像,也可能会由于影像上地物类型分布不均衡,导致组合系数求解的精度不够,使合成的全色波段(panchromatic image,PAN)影像与实际不符,造成融合影像的光谱失真。针对以上两个问题,本文提出一种基于光谱和空间局部相关的改进算法SSCSVR(spectral and spatial correlation-based synthetic variable ratio)。
2 基于光谱与空间局部相关融合方法原理
2.1 SVR算法原理与问题分析
文献[24]提出的SVR影像融合方法,出发点是低分辨率全色影像能够利用多光谱影像合成
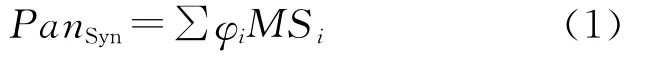
式中,PanSyn是合成的全色影像灰度值;MSi是要融合的多光谱影像中第i波段的灰度值;φi是第i波段的权系数值。
另一方面,SVR方法认为高分辨率全色影像和合成的低分辨率全色影像的比值反映了全色影像和多光谱影像的细节差异,如果把这些差异按比例分布到多光谱影像的各个波段,就可以生成和全色影像分辨率一致的高分辨率多光谱影像
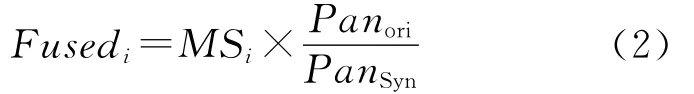
式中,Fusedi是融合后影像中第i波段的灰度值;Panori是原始的全色影像灰度值。
根据全色影像和多光谱影像的线性组合假设,全色影像合成的权系数φi可通过式(3)得到
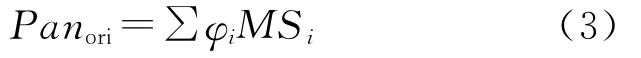
文献[24]利用城区、土壤、水、草地和树木5类地物来求取权系数φi。
文献[9]对SVR的方法进行进一步研究,明确了合成全色影像的多光谱波段应该是全色波段覆盖的波段,而不一定是多光谱影像的全部波段。同时,文献[9]认为求合成系数φi不能仅仅由指定的5类地物来求解,而应该利用影像的全部整体信息来求解。为此,文献[9]的改进算法采用了直方图归一化、融合后影像直方图重新拉伸等处理,使SVR成为一类具有独特意义的实用算法。然而对于不满足光谱覆盖条件的影像,SVR[9]会造成融合影像的光谱扭曲[23]。另外,对于满足光谱覆盖条件的影像,也可能会由于影像上地物类型分布的不均衡,导致组合系数求解的精度不够,使合成的PAN影像与实际不符,造成融合影像的光谱失真。
综合分析文献[9]的SVR算法,导致偏色的原因有:① 合成的PAN只考虑光谱相关而没有考虑空间相关,导致合成PAN不准确,引起偏色,尤其当多光谱波段与PAN波段不能完全相互覆盖时,偏色情况更为严重;② 对多光谱和全色波段进行直方图的归一化,这样可能会引起光谱信息的损失,引起偏色问题;③ 算法中要求合成的PAN与原始的PAN灰度值尽量接近,但是利用影像的整体信息来计算权值,会引起局部模拟的全色和原始全色影像光谱有较大不同,从而引起偏色问题。
本文基于光谱与空间局部相关的算法就是针对上述问题提出的。2.2.1节提出的光谱与空间相关模型能够更加严密地合成PAN值,克服第1个偏色原因;2.2.2节提出的自适应的局部处理和2.2.3节提出的非负约束最小二乘求解及异常处理方法可以有效地解决第2、3个偏色问题。
2.2 改进的基于光谱与空间局部相关的SVR方法融合原理
2.2.1 改进的光谱与空间相关模型
融合中光谱的保持与多光谱波段结构有关,而空间细节的保持与波段内的空间结构有关。计算PanSyn时,传统的SVR只考虑了PAN与多光谱波段的关系,但影像中像元之间是空间相关的,如果一个像元对融合影像有贡献,这个像元周围的像元也会对融合影像有贡献。PAN波段覆盖范围一般较大,不仅含有多光谱影像的光谱信息而且含有多于多光谱影像的空间细节信息。基于以上分析,本文提出了改进的空间与光谱相关的回归模型,模型见公式(4)。该模型能够更好地描述高空间分辨率的PAN与低分辨率的多光谱之间的关系,得到更准确的权值,从而得到更加准确的合成PAN值
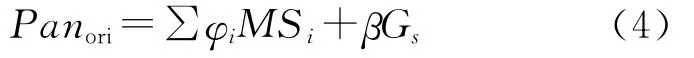
式中,β是空间相关成分的权值;Gs是空间相关成分信息即高频成分。式(4)的矩阵形式如式(5)所示

式中,X=[φ1φ2…φNβ]T为待求的权系数矩阵;N为多光谱影像的波段数,B=[MS1MS2…MSNGs]为已知的光谱和空间成分。
为了更好地获得高频成分Gs,笔者选用了高斯函数卷积的方法。高斯函数具有低通性质,并且可以模拟人眼视觉机理,通过不同的尺度参数σ设定,能够模拟人眼远近处所看到的图像。高斯函数表达式为
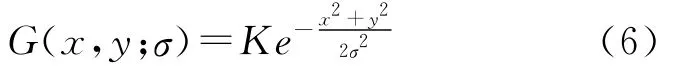
式中,系数K为归一化值。将高斯函数与影像进行卷积,可以得到低频信息,从原始影像中减去低频信息,即可得到高频信息Gs,⊗表示卷积操作,Gs的计算见式(7)
高斯核窗口r和尺度参数σ会直接影响到提取空间细节成分,进而影响光谱与空间相关权系数的求解。尺度参数σ越小提取的空间细节信息越少,反之尺度越大,提取的空间细节信息越多,但有可能出现过提取的情况。综合考虑空间细节提取的程度,本文采用标准高斯分布的σ值即σ=1。高斯核窗口r越大,Gs高频细节信息越多,但是计算量大,反之亦然,根据误差3σ规则,本文高斯核窗口r=3σ。
2.2.2 自适应的局部处理方法
在地物类型分布严重不均衡的情况下,利用影像的整体信息来计算权值,会引起合成的全色和原始全色影像光谱存在较大不同,从而引起偏色问题。考虑到影像像元的空间差异性,局部处理可能会比全局处理具有更大的优势。因此,本文将整个影像分为很多影像块,利用每个影像块里面的像素分别建立2.2.1中的光谱与空间相关回归模型,并采用非负的最小二乘方法进行求解,得到每个影像块里像素的光谱与空间相关权值,从而得到合成的全色PAN值。设h和l分别为PAN和MS的空间分辨率,则r=l/h为两者空间分辨率的比值,综合考虑融合效果与处理效率,分块大小w本文试验中取w=5r+1。
局部分块优化处理往往会产生分块效应,综合考虑融合效果和时间复杂度的影响,采用双线性内插来获得每个像素的权值,从而得到每个像素的合成PAN值。
2.2.3 非负约束最小二乘求解及异常情况处理
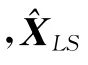
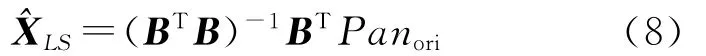
本文采用非负约束最小二乘方法进行求解,可以使求解的系数非负,使系数具有物理意义。非负约束最小二乘是一种较为成熟的优化理论,原理描述如下
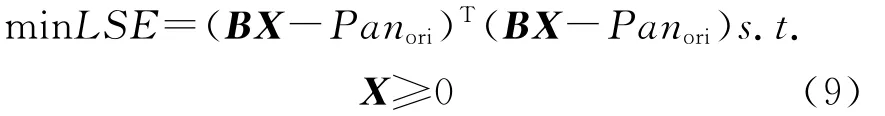
式中,LSE为非负约束的优化误差;X≥0表示对于所有的1≤k≤N+1都有xk≥0。为了应用拉格朗日方法解求优化问题,引入N+1维未知的被动约束常量c=[c1c2…cN+1]T>0,ck>0,k的取值为1,2,…,N+1。通过c,可以形成拉格朗日式J
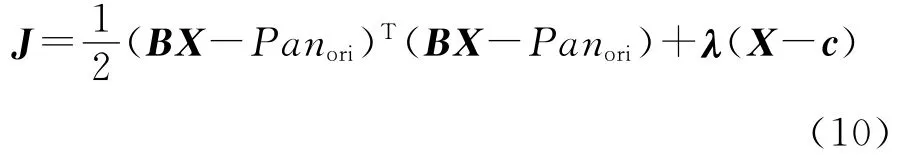
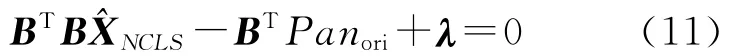
从式(11)可得出式(12)和式(13)
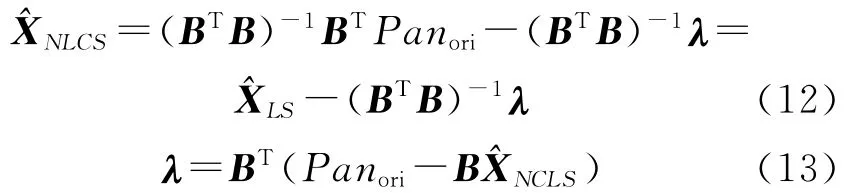
式(12)和(13)可以用来解求非负约束优化解^XNCLS和拉格朗日系数λ=[λ1λ2…λN+1]T。
本文求解系数采用了快速非负约束最小二乘(fast non-negativity-constrained least squares,FNNLS)算法,详细介绍见文献[25]。该算法的主要思想是将估计量分离为活动集R和被动集P,前者包括中所有负值和零值,后者包括所有剩余的正值。FNNLS处理开始时被动集P为空集,假设活动集R包括中所有元素,通过式(12)和(13)迭代处理调节活动集和被动集。具体实施时,迭代结束条件可设为活动集R为空集或者活动集R不为空集且所有拉格朗日系数λk,k∈R为负值。
利用FNNLS算法求解权系数矩阵过程中可以看出需对实对称矩阵求逆,此时,要考虑该矩阵是否可逆的问题,如果该矩阵可逆,则可以利用FNNLS方法较容易地求得准确的权系数,反之则需进行异常情况的处理。通过试验发现实对称矩阵不可逆是由于用来求解系数的像素灰度值变化不大,非常接近,如大片水的区域容易发生这种情况。当系数求解不出时,采用式(14),即系数等于块内所有全色像素的和的比值与所有多光谱像素的和
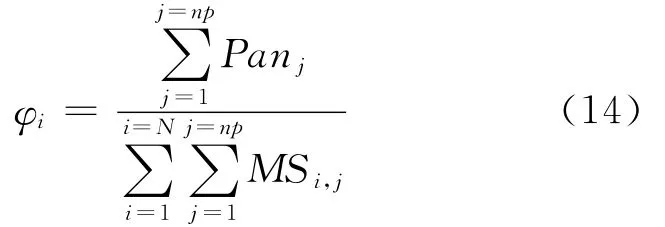
式中,np为用于求解系数的像素个数;j的取值范围为1,2,…,np;Panj是全色影像第j个像素的灰度值;MSi,j是多光谱影像第i波段第j个像素的灰度值。一般用于求解系数的像素采用影像块内所有像素,np=w×w。
3 试验结果与分析
选取意大利罗马地区的 WorldView-2影像作为试验数据,影像数据包括1个空间分辨率0.5m的全色波段和8个空间分辨率2m的多光谱波段,全色影像大小为4600像素×4604像素,多光谱影像大小为1150像素×1151像素。试验区域为城市区域,包括植被、建筑物、道路、水体等地物类型。
图1(a)为试验区的待融合全色影像,图1(b)为经过严格空间配准和重采样后的待融合多光谱影像。为了评价本文方法,采用Gram-Schmidt[5]、HCS[6]和 SVR[9]方法进行对比。图1(c)为本文SSCSVR方法融合后的影像。鉴于篇幅限制,在此只列出本文方法融合后的结果。图1(d)~(i)分别为待融合全色影像(图中绿框区域)、多光谱影像以及本文SSCSVR、HCS、Gram-Schmidt和SVR[9]融合后影像的局部放大图。影像以波段(5,3,2)显示的(R,G,B)。与原始多光谱影像相比,4种融合方法的空间分辨率都有明显的提高,细节得到了增强,达到了很好的空间分辨效果。但是从光谱色彩来看,Gram-Schmidt和SVR[9]方法整体光谱扭曲比较严重,整个影像偏红,灰色的道路颜色偏白,暗黑色区域偏蓝。分析SVR[9]方法偏色的原因主要是:影像中房屋红色偏多,Zhang SVR利用整体信息求解出的权系数红色成分偏大,导致道路和暗黑色小区域严重偏色,并且使影像整体偏色严重。WorldView-2的全色波段与多光谱(或部分波段)不能互相完全覆盖,导致SVR[9]求解出的系数不能准确描述全色与多光谱影像之间的关系。本文采用光谱与空间相关局部优化策略,克服了以上缺点。HCS是处理 WorldView-2卫星影像的官方处理方法,本文方法不仅光谱保持程度可以和HCS方法相媲美,能保持地物的原来色彩,达到了很好的视觉效果,而且在空间细节方面比HCS要好,如图红框区域,通过仔细查看可以看出HCS方法处理结果丢失了部分细节,而本文SSCSVR方法细节明显。
ERGAS(relative global-dimensional synthesis error)[26]可以客观地评价融合影像的整体光谱质量,偏差指数反映影像的偏色水平,SSIM(structure similarity index Measurement)[27]可以较好地评价光谱结构特征,信息熵反映影像空间细节情况。这4个客观评价指标可以较好地评价融合后影像的光谱和空间特征,且较为常用。因此,为了客观定量评价文中各方法,本文选取了这4个评价指标。ERGAS和偏差指数值越小说明光谱保持越好;SSIM值越大说明光谱结构越相似,质量越好;信息熵反映影像空间细节情况,熵值越大说明影像所含的信息量越多。原始多光谱影像平均信息熵5.382,全色影像信息熵5.567。表1列出了各种融合方法定量评价的结果,从表中可以看出各种方法的融合结果信息熵都有所提高,从而到达了融合的目的。Gram-Schmidt和SVR[9]的各项指标比较相近,ERGAS和偏差指数较高,而SSIM值偏低,说明这两种方法光谱扭曲程度较大,而信息熵值较低,说明影像包含信息较少。从ERGAS、SSIM和偏差指数可以看出HCS和SSCSVR两个方法都能较好地保持光谱特征且能够保持原来光谱的内部结构,从信息熵可以看出SSCSVR比HCS信息含量稍微高一点,充分验证了目视评价中HCS空间细节稍逊于本文方法SSCSVR的说法。

图1 WorldView-2影像融合结果Fig.1 Fusion results of WorldView-2images
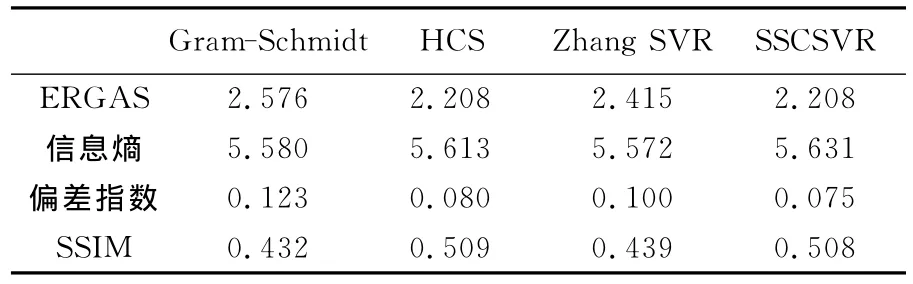
表1 各方法融合结果的定量评价Tab.1 Quantitative assessments of fusion results
从目视和客观评价可以看出本文SSCSVR方法较SVR[9]光谱和空间细节方面都有一定提高,充分克服了SVR方法本身光谱扭曲的缺陷。
为了充分说明本文方法的正确性,笔者又选用了另外一组QuickBird的印度地区数据,影像包括5个波段,4个多光谱波段,空间分辨率2.44m,1个全色波段,空间分辨率0.61m。全色影像大小为6000像素×6000像素,多光谱影像大小为1500像素×1500像素。试验区域为城市区域,包括水体、植被、建筑物和道路等地物类型。融合结果如图2所示,以波段(3,2,1)显示的(R,G,B)。

图2 QuickBird影像融合结果Fig.2 Fusion results of QuickBird images
从图2可以看出,SVR[9]方法存在较为严重的光谱偏差,整体影像偏绿,偏白,HCS绿色有点偏蓝,Gram-Schmidt方法影像偏绿,围栏区域偏白而SSCSVR光谱保持较好,4种方法空间细节上看不出什么明显的差别。定量比较结果见表2,SSCSVR各项指标都最优。从综合上来看,SSCSVR的融合结果是最好的,这一结论与WorldView-2融合试验的结论一致。通过试验可以证明,即使当全色波段与多光谱波段完全覆盖时,由于影像质量本身的原因(QuickBird影像中地物类型分布不均衡,全色影像细节较多),利用整体信息和只考虑光谱相关求解出的权系数不准确,导致SVR[9]的融合结果不是很理想,而本文方法则较好地克服了这一点。
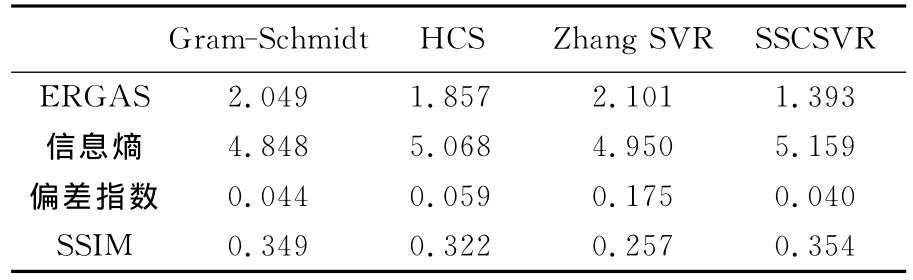
表2 各方法融合结果的定量评价Tab.2 Quantitative assessments of fusion results
笔者也对其他传感器影像如Spot-5、IKONOS、Landsat-7、GeoEye-1作了类似试验,可以得出与文中一样的结论,验证了本文方法的优越性。
4 结 论
本文针对传统SVR方法存在光谱扭曲问题,提出了一种基于光谱与空间局部相关的光谱和空间保持型影像融合方法。与传统SVR方法不同的是,该方法不需要将全色和多光谱影像进行直方图归一化,因此能更好地保护空间和光谱信息,也无须严格满足全色与多光谱相互覆盖的条件。该方法用于 WorldView-2等卫星的全色和多光谱影像融合试验中,能够得到空间细节与光谱信息保持度高的融合影像,能适应不同传感器的特点和地物分布情况。
[1] THOMAS C,RANCHIN T,WALD L,et al.Synthesis of Multispectral Images to High Spatial Resolution:A Critical Review of Fusion Methods Based on Remote Sensing Physics[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(5):1301-1312.
[2] BARONTI S,AIAZZI B,SELVA M,et al.A Theoretical Analysis of the Effects of Aliasing and Misregistration on Pansharpened Imagery[J].Journal of Selected Topics in Signal Processing,2011,5(3):446-453.
[3] CHIKR EL-MEZOUAR M,TALEB N,KPALMA K,et al.An IHS-Based Fusion for Color Distortion Reduction and Vegetation Enhancement in IKONOS Imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(5):1590-1602.
[4] PAT S C J,STUART S C,JEFFREY A A.Comparison of Three Different Methods to Merge Multiresolution and Multispectral Data:Landsat TM and SPOT Panchromatic[J].Photogrammetric Engineering and Remote Sensing,1991,57(3):295-303.
[5] LABEN C A,BROWER B V.Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening:United States,6011875[P].2000.
[6] PADWICK C,PACIFICI F,SMALLWOOD S.WorldView-2 Pan-Sharpening[C]∥ASPRS 2010Annual Conference.San Diego:[s.n.],2010.
[7] JAEWAN C,KIYUN Y,YONGIL K.A New Adaptive Component-Substitution-Based Satellite Image Fusion by Using Partial Replacement[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(1):295-309.
[8] GILLESPIE A R,KAHLE A B,WALKER R E.Color Enhancement of Highly Correlated Images.II.Channel Ratio and"chromaticity"Transformation Techniques[J].Remote Sensing of Environment,1987,22(3):343-365.
[9] ZHANG Yun.System and Method for Image Fusion:United States,7340099B2[P].2008.
[10] OTAZU X,GONZALEZ-AUDICANA M,FORS O,et al.Introduction of Sensor Spectral Response into Image Fusion Methods.Application to Wavelet-based Methods[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(10):2376-2385.
[11] PRADHAN P S,KING R L,YOUNAN N H,et al.Estimation of the Number of Decomposition Levels for a Wavelet-Based Multiresolution Multisensor Image Fusion[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(12):3674-3686.
[12] CUNHA A L,ZHOU Jianping,DO M N.The Nonsubsampled Contourlet Transform:Theory,Design,and Applications[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.
[13] GANGKOFNER U G,PRADHAN P S,HOLCOMB D W.Optimizing the High-Pass Filter Addition Technique for Image Fusion[J].Photogrammetric Engineering and Remote Sensing,2008,74(9):1107-1118.
[14] BAI Xiangzhi,ZHOU Fugen,XUE Bindang.Edge Preserved Image Fusion based on Multiscale Toggle Contrast Operator[J].Image and Vision Computing,2011,29(12):829-839.
[15] XU Min,CHEN Hao,VARSHNEY P K.An Image Fusion Approach Based on Markov Random Fields[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(12):5116-5127.
[16] LIU Jun,SHAO Zhenfeng.Remote Sensing Image Fusion Using Multi-scale Spectrum Gain Modulation[J].Acta Geodaetica et Cartographica Sinica,2011,40(4):470-476.(刘军,邵振峰.基于多尺度光谱增益调制的遥感影像融合方法[J].测绘学报,2011,40(04):470-476.)
[17] CHU Heng,WANG Ruyan,ZHU Weile.Remote Sensing Image Fusion Algorithm in the DCT Domain[J].Acta Geodaetica et Cartographica Sinica,2008,37(1):70-76.(楚恒,王汝言,朱维乐.DCT域遥感影像融合算法[J].测绘学报,2008,37(1):70-76.)
[18] JOSHI M,JALOBEANU A.MAP Estimation for Multiresolution Fusion in Remotely Sensed Images Using an IGMRF Prior Model[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(3):1245-1255.
[19] YU Nannan,QIU Tianshuang,BI Feng,et al.Image Features Extraction and Fusion Based on Joint Sparse Representation[J].IEEE Journal of Selected Topics in Signal Processing,2011,5(5):1074-1082.
[20] YANG Bin,LI Shutao.Pixel-Level Image Fusion with Simultaneous Orthogonal Matching Pursuit[J].Information Fusion,2012,13(1):10-19.
[21] LI Shutao,YANG Bin.A New Pan-Sharpening Method Using a Compressed Sensing Technique[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(2):738-746.
[22] JIANG Cheng,ZHANG Hongyan,SHEN Huanfeng,et al.A Practical Compressed Sensing-Based Pan-Sharpening Method[J].Geoscience and Remote Sensing Letters,2012,9(4):629-633.
[23] ALPARONE L,WALD L,CHANUSSOT J,et al.Comparison of Pansharpening Algorithms:Outcome of the 2006GRS-S Data-Fusion Contest[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(10):3012-3021.
[24] MUNECHIKA C K,WARNICK J S,SALVAGGIO C,et al.Resolution Enhancement of Multispectral Image Data to Improve Classification Accuracy[J].Photogrammetric Engineering and Remote Sensing,1993,59(Compendex):67-72.
[25] BRO R,JONG S.A Fast Non-Negativity-Constrained Least Squares Algorithm[J].Journal of Chemometrics,1997,11:393-401.
[26] WALD L.Data Fusion:Definitions and Architectures Fusion of Images of Different Spatial Resolutions[M].Paris:Presses de l′Ecole,Ecole des Mines de Paris,2002.
[27] WANG Zhou,BOVIK A C,SHEIKH H R,et al.Image Quality Assessment:from Error Visibility to Structural Similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.
