基于矩谐分析的航空重力向下延拓

蒋 涛，党亚民，章传银，刘站科

1.中国测绘科学研究院，北京 100830；2.国家测绘地理信息局 第一大地测量队，陕西 西安 710054

1 引 言

经济高效的航空重力测量能够很好地填补卫星重力和地面重力测量所得重力场信息的信号盲区，可覆盖地面重力测量难以达到的地区，数据精度在全波长为5～10km的空间分辨率尺度上能够达到1～3mGal（1Gal＝1cm／s2）。航空重力测量获取的是距地面达数千米飞行高度处的重力观测值，大地测量和地球物理等领域需要的是地面或大地水准面上的重力值，因此需将飞行高度处的重力观测值向下调和延拓至地面或大地水准面上。

在航空重力观测值向下延拓过程中噪声会得到放大，可能造成重力场信号的严重失真，若不采用合适的向下延拓方法，将无法得到稳定可靠的重力延拓解。现有的向下延拓方法主要包括逆泊松积分法［1－7］、最小二乘配置（LSC）［8］、快速傅里叶变换（FFT）［9-10］、直接代表法［11］和直接法［12－13］，其中比较常用的是逆泊松积分法，求解泊松积分方程时一般需引入正则化处理。

本文提出了一种基于矩谐分析的航空重力向下延拓新方法，矩谐分析最开始被文献［14—15］用于区域地磁场建模，在地磁学研究中应用广泛。文献［16］将矩谐分析用于局部重力场逼近，数值结果验证了其可行性。该方法的基本原理是在局部直角坐标系中将扰动位或其泛函展开成矩谐级数，利用飞行高度处的重力异常或重力扰动进行矩谐分析以求解表征该区域内重力场的扰动位系数，再进行矩谐综合计算得到地面或大地水准面上的重力异常和重力扰动，从而完成重力观测值从飞行高度处到地面或大地水准面的向下调和延拓。本文利用EGM2008重力位模型［17］设计模拟数值试验，将矩谐分析与直接法和基于广义岭估计的逆泊松积分法作数值比较分析，验证了基于矩谐分析的向下延拓方法的可靠性、精度和稳定性。

2 数学模型

矩谐分析表达区域地球重力场的基本思想是在局部直角坐标系下求解拉普拉斯方程，将引力位展开成矩谐级数，以矩谐系数的集合来表征引力位。矩谐分析是在局部直角坐标系中进行的，因此需选取数据区域的中心点作为局部直角坐标系的原点，将输入数据点的大地坐标或球坐标转换到局部直角坐标系中。图1以航空重力测量数据为例，给出了局部直角坐标系下区域重力场表达的几何关系。

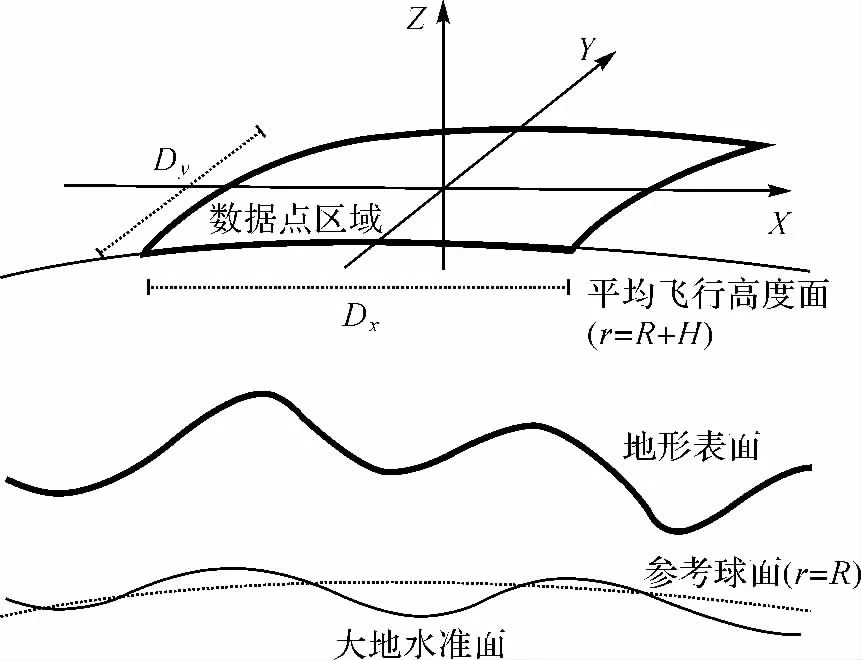
图1 局部直角坐标系下区域重力场表达的几何关系Fig.1 Geometry of the regional gravity field representation in local Cartesian coordinate system

在航空重力测量中，GPS动态定位能够精密确定飞行高度处的大地高，重力扰动的获取已不成问题，可采用重力扰动作为重力观测值。在此直接给出重力扰动的矩谐展开式，推导过程请参见文献［18］

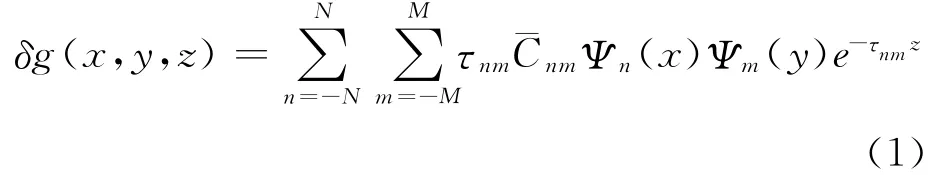
式中

式（1）中的τnm定义为

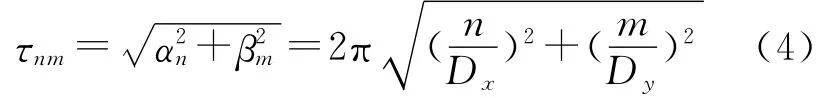
式中，Dx、Dy分别表示矩形计算区域在东西（x）和南北（y）方向上的距离（见图1）。矩谐展开式（1）对应的半波长空间分辨率为

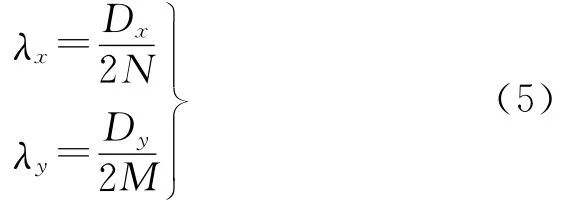
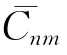
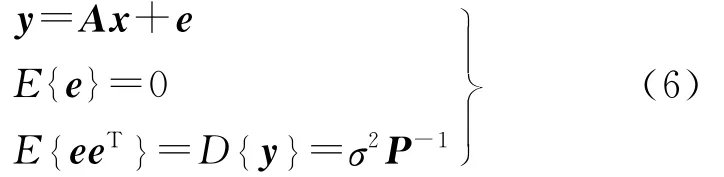
式中，y为k阶空中重力扰动观测值向量；A为k×u阶设计矩阵；x为u阶待求扰动位系数向量；e为观测噪声，其数学期望为0；D｛y｝ 为观测值的方差—协方差阵；σ2是先验方差因子；P是权阵，对应的法方程为

其最小二乘解为

矩谐展开模型（1）采用周期性函数傅里叶级数表达重力场信号，其成立的前提是假定待求信号在计算区域内也是周期性的。显然有限区域的重力场信号不具有完全的周期性，用周期函数表示非周期性信号，在区域的边界处，重力位近似等于两边界处重力位的平均值，会产生周期延拓边界效应。在矩谐分析中，扩展计算区域的范围，使计算区域内的待求重力场信号满足周期性条件，可降低周期延拓边界效应的影响。若数据点平面范围为Dx和Dy（如图1），将计算区域的平面范围扩展为Dx＋Δx和Dy＋Δy，使得待估重力场信号在区间D＋Δ上满足周期性条件，可显著降低边界效应，于是式（4）应改写为

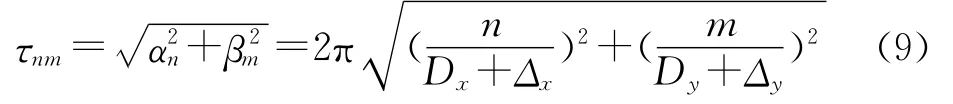
航空重力数据在向下延拓过程中观测噪声会被放大。随着数据格网间隔的减小和延拓高度的增加，设计矩阵A（式（7））的复共线性增强，有可能呈病态甚至奇异，若采用经典最小二乘方法求解，即使较小的观测误差也会导致解的严重失真甚至错误。此外，在矩谐分析中引入扩展参数Δ也会使法方程（式（7））的条件数增加，加重法方程的病态性，同样会影响待求扰动位系数的求解精度。因此，必要时需引入正则化方法求解病态法方程，以获取待求位系数的最优解，可采用Tikhonov正则化方法，则式（6）的正则化解为

式中，I为单位阵；α＞0为正则化参数，至于最优正则化参数的确定可采用广义交叉检验（GCV），详细算法请参见文献［6］、［19］。

利用飞行高度处的重力扰动观测值进行矩谐分析求得表示该区域内重力场的扰动位系数后，再按照式（1）进行矩谐综合计算即可得到大地水准面上的重力扰动，至此便完成了航空重力观测值的向下延拓。

3 数值计算与分析

为评价基于矩谐分析的向下延拓方法的可靠性、精度和稳定性，利用EGM2008重力位模型设计模拟数值试验，将矩谐分析与直接法［13］和基于广义岭估计的逆泊松积分法［6］这两种下延方法进行数值比较与分析。首先利用EGM2008重力位模型的2～2190阶位系数计算得到飞行高度处的重力扰动，在模拟观测值中加入数学期望为0、标准差为1.5mGal的高斯白噪声，移去由GOCE卫星重力位模型［20］2～120阶位系数计算的参考重力扰动得到残余重力扰动，将残余重力扰动向下延拓至大地水准面得到延拓值，再恢复参考模型值得到大地水准面上的重力扰动延拓值。将由EGM2008模型2～2190阶位系数计算的大地水准面上的重力扰动作为真实值，比较重力扰动延拓值与真实值，可以检验向下延拓方法的可靠性与精度并比较其优劣。为模拟真实航空重力测量条件，选定4个飞行高度H（正高），分别是2km、3km、4km、5km，数据点范围为纬线［30°，33°］和经线［107°，110°］围成的3°×3°区域，格网间隔取2.5′×2.5′，共包含5184个数据点，重力扰动模拟观测值统计信息见表1。分别采用矩谐分析、直接法和基于广义岭估计的逆泊松积分法，将飞行高度处的重力扰动观测值向下延拓至大地水准面。直接法和逆泊松积分法采用EGM96重力位模型计算远区流动点的贡献，最大阶数截断至360阶，积分球冠区半径选为1°。经多次对比测试，确定了矩谐分析的最优展开阶数和扩展参数，展开阶数取为N＝M＝20，扩展参数取为Δ＝50km，选择GCV方法确定正则化参数。

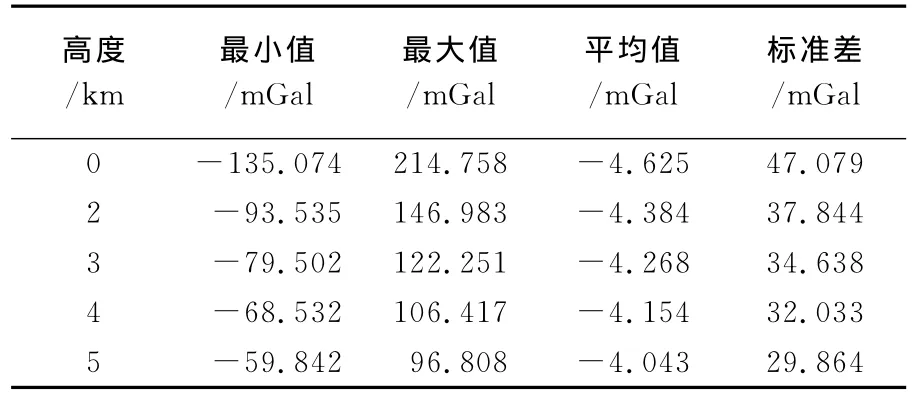
表1 重力扰动模拟观测值统计表Tab.1 Statistics of simulated gravity disturbance

由于计算区域外没有数据点分布，直接法、逆泊松积分法和矩谐分析的向下延拓结果均会受到边界效应影响，矩谐分析中还存在周期延拓边界效应，首先对比这3种下延方法的边界效应。图2是直接法、基于广义岭估计的逆泊松积分法和矩谐分析的向下延拓误差分布图，延拓高度为4km，计算点范围与数据点范围保持一致。可以看出，在这3种方法中，矩谐分析的下延结果受边界效应的影响最小，误差极值点的数量和量级是最小的，主要分布在距四周边界15′以内，中心区域（图2中虚线围成的2°×2°矩形）计算点的结果不受边界效应影响。直接法的边界效应最为严重，误差极值点的数量和量级均大大超过其他两种方法，即使在中心区域误差也非常明显。基于广义岭估计的逆泊松积分法的边界效应介于矩谐分析和直接法之间，中心区域的计算点基本不受边界效应影响。

为消除边界效应的影响，应以2°×2°中心区域的计算结果来评定3种向下延拓方法的精度，共包含2304个计算点。表2分别给出了取不同延拓高度时直接法、逆泊松积分法和矩谐分析的向下延拓误差统计信息，向下延拓误差定义为延拓值与由EGM2008模型计算的真实值之差，其中误差比定义为

式中，RMS为延拓值相对于真实值的均方根误差；e为白噪声的标准差。可以看出，在不同延拓高度处，矩谐分析所得延拓解的精度都是最高的，RMS随延拓高度的增大幅度也是最小的，最大误差比仅为2.12，噪声放大程度远低于直接法，略低于基于广义岭估计的逆泊松积分法。当延拓高度为5km时，矩谐分析解的RMS为3.183mGal，占直接法所得延拓值RMS（5.665mGal）的56%，略低于逆泊松积分法所得延拓解的RMS（3.245mGal）。图3是2°×2°中心区域内3种方法的向下延拓误差分布图，延拓高度为4km。从中可以看出，矩谐分析的向下延拓误差均在±10mGal以内，大部分计算点处的误差不超过±3mGal，其空间分布与逆泊松积分法相似，但误差量级略低。相比之下，直接法的向下延拓效果最差，中心区域受到边界效应的影响，出现了较多误差极值点。

图2 不同方法的向下延拓误差Fig.2 DWC errors of different methods

图3 2°×2°中心区域不同方法的向下延拓误差Fig.3 DWC errors of different methods in 2°×2°central area

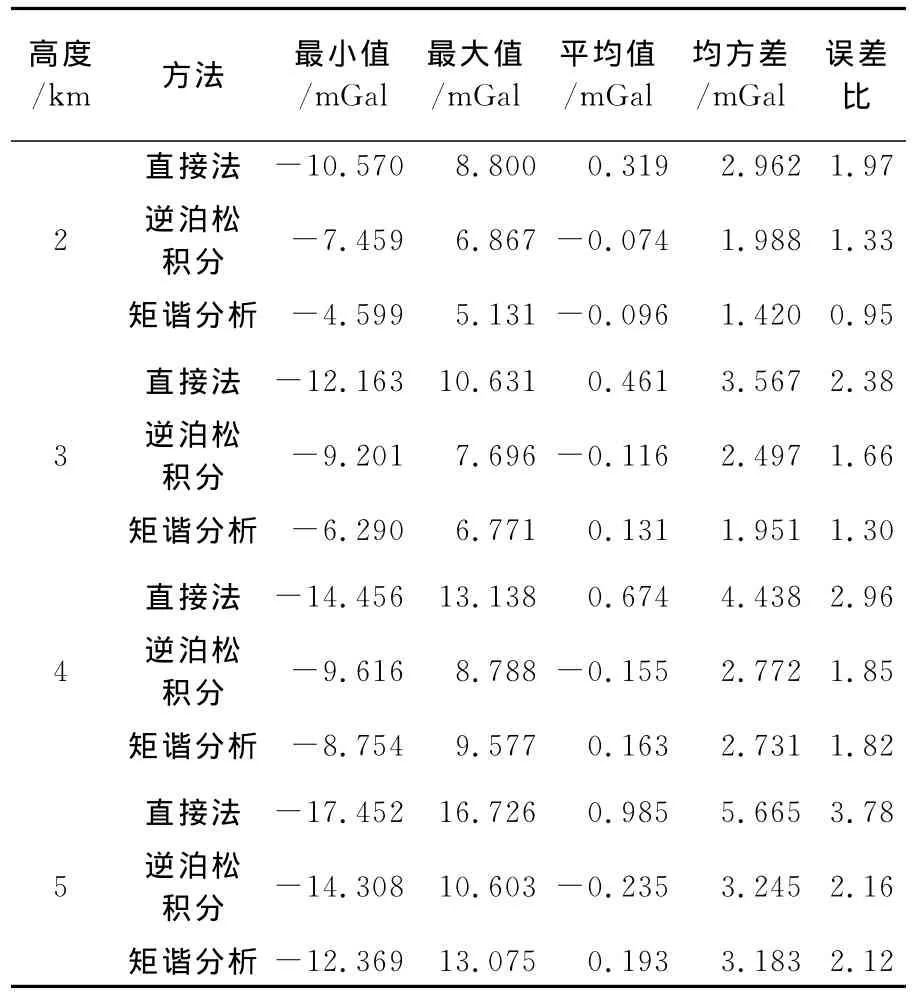
表2 不同飞行高度的向下延拓误差统计Tab.2 Statistics of the DWC errors at different flight levels

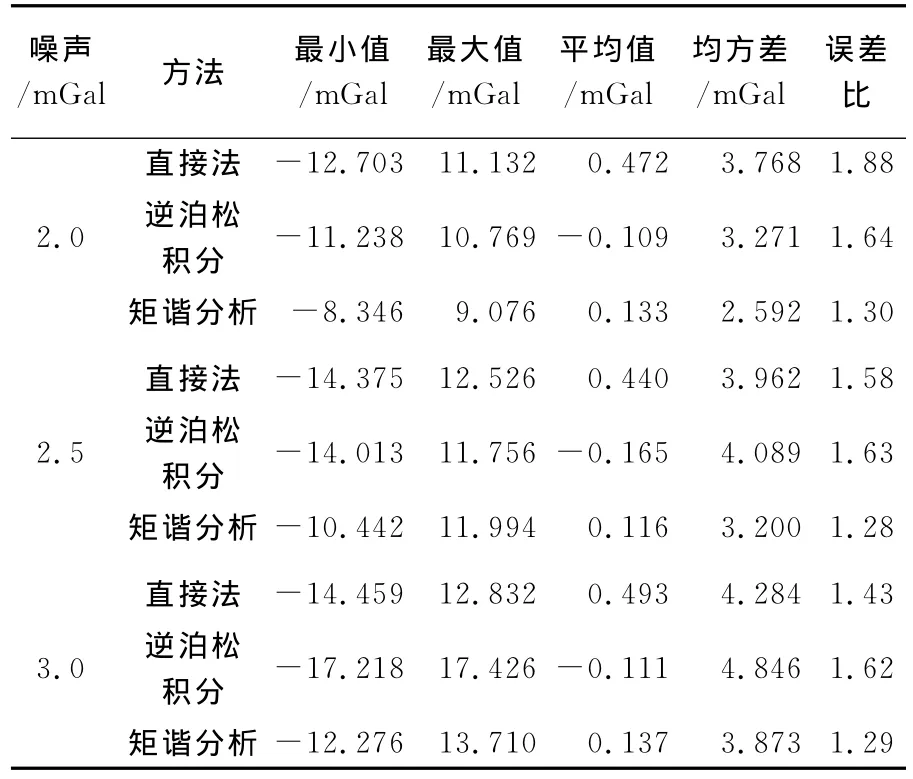
表3 加入不同量级噪声时的向下延拓误差统计Tab.3 Statistics of the DWC errors with different noise levels

以上数值结果都是在标准差为1.5mGal的高斯白噪声条件下得到的，为检验含较大量级噪声时3种向下延拓方法的可靠性与精度，分别在重力扰动观测值中加入标准差为2mGal、2.5mGal和3mGal的高斯白噪声进行向下延拓计算。表3分别给出了加入不同量级噪声时直接法、逆泊松积分法和矩谐分析的向下延拓误差统计信息，延拓高度取3km，总体上仍然是矩谐分析表现最优，具有最好的精度和稳定性。数值比较结果表明矩谐分析能够有效抑制测量噪声的放大，实现航空重力信号的稳定向下延拓，在精度、稳定性和边界效应等方面都要优于直接法和基于广义岭估计的逆泊松积分法。

4 结 论

矩谐分析通过在局部直角坐标系下求解关于引力位的拉普拉斯方程，建立位系数与重力观测值之间的函数关系，其推导过程严格满足地球重力场的位理论，具有明确的物理意义。实际计算时矩谐函数展开至一定的截断阶次，求得表征区域重力场结构的有限阶次矩谐系数，在谱域内对重力场信号具有一定的平滑作用，在求解关于扰动位系数的线性方程组（6）时，又引入了正则化处理，故矩谐分析能够有效抑制向下延拓过程中观测噪声的放大。

直接法和逆泊松积分法属于空域内的向下延拓方法，由于其函数模型的固有局限性，下延结果的边界效应比较明显，特别是直接法的结果受边界效应影响非常严重。矩谐分析方法同样存在边界效应，但扩展计算区域的范围，求解法方程时进行正则化处理，可有效控制边界效应的量级和影响范围，使得中心区域不致受到边界效应的影响。基于EGM2008重力位模型设计的空中重力数据向下延拓数值试验表明：在下延精度、稳定性和边界效应等方面，矩谐分析都要优于直接法和基于广义岭估计的逆泊松积分法，能够实现航空重力数据的稳定下延，是一种可靠的航空重力向下延拓方法。

［1］ MARTINE C Z.Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains ［J］.Journal of Geodesy，1996，70：805－828.

［2］ VANÍCEK P，SUN W，ONG P，et al.Downward Continuation of Helmert’s Gravity［J］.Journal of Geodesy，1996，71：21－34.

［3］ SUN W，VANÍCEK P.On Some Problems of the Downward Continuation of the 5′×5′Mean Helmert Gravity Disturbance［J］.Journal of Geodesy，1998，72：411－420.

［4］ WANG Xingtao，SHI Pan，ZHU Feizhou.Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data［J］.Acta Geodaetica et Cartographica Sinica，2004，33（1）：33－38.（王兴涛，石磐，朱非洲.航空重力测量数据向下延拓的正则化算法及其谱分解 ［J］.测绘学报，2004，33（1）：33－38.）

［5］ GU Yongwei，GUI Qingming.Study of Regularization Based on Signal to Noise Index in Airborne Gravity Downward to the Earth Surface ［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：458－464.（顾勇为，归庆明.航空重力测量数据向下延拓基于信噪比的正则化方法的研究［J］.测绘学报，2010，39（5）：458－464.）

［6］ JIANG Tao，LI Jiancheng，WANG Zhengtao，et al.The Solution of Ill－posed Problem in Downward Continuation of Airborne Gravity ［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：684－689.（蒋涛，李建成，王正涛，等.航空重力向下延拓病态问题的求解 ［J］.测绘学报，2011，40（6）：684－689.）

［7］ DENG Kailiang，HUANG Motao，BAO Jingyang，et al.Tikhonov Two－parameter Regularization Algorithm in Downward Continuation of Airborne Gravity Data ［J］.Acta Geodaetica et Cartographica Sinica，2011，40 （6）：690－696.（邓凯亮，黄谟涛，暴景阳，等.向下延拓航空重力数据的Tikhonov双参数正则化法 ［J］.测绘学报，2011，40（6）：690－696.）

［8］ FORSBERG R，KENYON S.Evaluation and Downward Continuation of Airborne Gravity Data：The Greenland Example［C］∥Proceedings of International Symposium Kinematic Systems in Geodesy，Geomatics and Navigation.Banff：［s.n.］；1994：531－538.

［9］ BÁLHA T，HIRSCH M，KELLER W，et al.Application of a Spherical FFT Approach in Airborne Gravimetry［J］.Journal of Geodesy，1996，70：663－672.

［10］ HWANG C，HSIAO Y，SHIH H，et al.Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey：Data Reduction and Accuracy Assessment［J］.Journal of Geophysical Research，2007，112（2）：101－110.

［11］ SHI Pan，WANG Xingtao.The Frequence Domain Analysis for the Determination of Terrestrial Mean Gravity Anomaly Using Airborne Gravimetry ［J］.Acta Geodaetica et Cartographica Sinica，1995，24（4）：301－308.（石磐，王兴涛.空中测量地面平均重力异常的频域分析 ［J］.测绘学报，1995，24（4）：301－308.）

［12］ SHI Pan，SUN Zhongmiao.The Solution to the Problem of the Spherical Interior Dirichlet and Its Application［J］.Acta Geodaetica et Cartographica Sinica，1999，28（3）：195－198.（石磐，孙中苗.球内Dirichlet问题解及其应用［J］.测绘学报，1999，28（3）：195－198.）

［13］ NOVÁK P，HECK B.Downward Continuation and Geoid Determination Based on Band－limited Airborne Gravity Data［J］.Journal of Geodesy，2002，76：269－278.

［14］ ALLDREDGE L R.Rectangular Harmonic Analysis Applied to the Geomagnetic Field ［J］.Journal of Geophysical Research，1981，86（B4）：3021－3026.

［15］ LI Mingming，HUANG Xianlin，LU Hongqian，et al.Modeling of High Accuracy Local Geomagnetic Field Based on Rectangular Harmonic Analysis［J］.Journal of Astronautics，2010，31（7）：1730－1736.（李明明，黄显林，卢鸿谦，等.基于矩谐分析的高精度局部地磁场建模研究［J］.宇航学报，2010，31（7）：1730－1736.）

［16］ BIAN Shaofeng.Numerical Solution for Geodetic Boundary Value Problem and the Earth′s Gravity Field Approximation［D］.Wuhan：Wuhan Technical University of Surveying and Mapping，1992.（边少锋.大地测量边值问题数值解法和地球重力场逼近 ［D］.武汉：武汉测绘科技大学，1992.）

［17］ PAVLIS N K，HOLMES A，KENYON S C，et al.An Earth Gravitational Model to Degree 2160：EGM08［C］∥Proceedings of the 2008General Assembly of the European Geoscience Union.Vienna：［s.n.］，2008.

［18］ JIANG Tao.Regioanl Geoid Determination Using Airborne Gravimetry Data［D］.Wuhan：Wuhan University，2011.（蒋涛.利用航空重力测量数据确定区域大地水准面［D］.武汉：武汉大学，2011.）

［19］ KUSCHE J，KLEES R.Regularization of Gravity Field Estimation from Satellite Gravity Gradients［J］.Journal of Geodesy，2002，76：359－368.

［20］ BRUINSMA S L，MARTY J C，BALMINO G，et al.GOCE Gravity Field Recovery by Means of the Direct Numerical Method［C］∥Proceedings of the ESA Living Planet Symposium.Bergen：［s.n.］，2010.