有关圆的错例分析

江苏 陈日铭

同学们在学习圆时，由于认识和理解上的偏差，容易产生一些常见性错误。分析这些错误产生的原因，可以帮助我们正确计算有关圆的问题。

错例1：两端都在圆上的线段叫做直径。

错因分析：对“直径”的理解不够深刻和全面。少了“通过圆心”这一关键前提。

正确说法：通过圆心并且两端都在圆上的线段叫做直径。

错例2：大圆的圆周率大，小圆的圆周率就小。

错因分析：没有正确认识圆周率的意义。圆周率是圆的周长与它的直径的比值，它是一个固定的数，用字母表示，是一个无限不循环小数，≈3.14。不管大圆小圆都是这样，并不是大圆的圆周率大，小圆的圆周率就小。

正确说法：大圆的圆周率和小圆的圆周率相同。

错列3：用一段铁丝围成一个如图1的零件，求这个零件的周长。（单位：厘米）

图1

图2

错因分析：对“半圆的周长”与“圆周长的一半”这两个概念模糊不清。“圆周长的一半”如图2。“半圆的周长”应是圆周长的一半与半圆直径的和，如题中图形。题目要求这个零件的周长，实际是要我们求出半圆图的周长。

正确解法：3.1410 2+10=25.7（厘米）

错例4：一个运动场（如图3所示），两头是半圆形，中间是长方形，这个运动场的周长是多少？

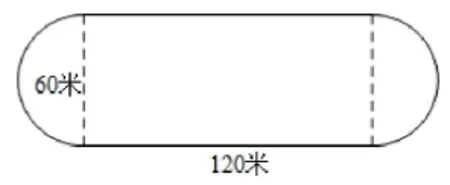
图3

错因分析：脱离实际，误把两个半圆的直径的长60米，当成运动员的路线，因而多算了两个60米。运动员要跑的路线，实际是两个120米和一个圆的周长。

正确解法：1202+3.1460=428.4（米）

错例5：计算图4中阴影部分的面积。（单位：厘米）

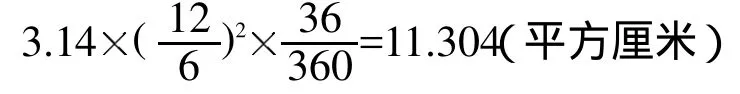
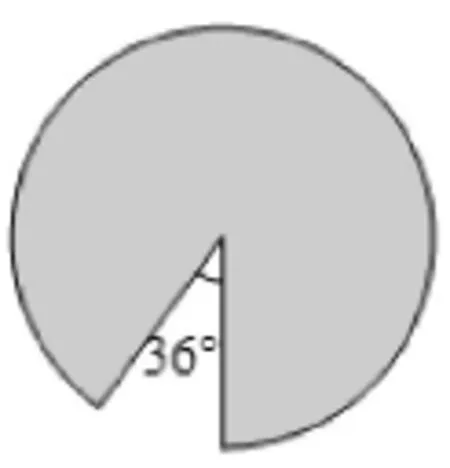
图4

错因分析：设有认真审题，走向了问题的反面。题目要求阴影部分面积，而求出的是空白部分面积。

错例6：公园里有一个圆形花圃，直径是10米，在花圃的周围修一条1米宽的石子路，这条石子路的面积是多少平方米？

错因分析：没有弄清题意。题目要求的是小路的面积，而实际求出的是花圃的面积与小路面积的和。小路的面积实际是一个环形面积。

正确解法：3.14[(10 2+1)2－（平方米）