“借”——解题的一种有效策略

☉广东省东莞市厚街湖景中学 毕道松

这则故事启示我们在解决数学问题时，如果也能够运用“借”的艺术，则可以使问题得到简捷而巧妙的解决.

一、借“物”

例1 已知4个矿泉水空瓶可以换矿泉水一瓶，现有15个矿泉水空瓶，若不交钱，最高可以喝矿泉水（ ）瓶.

A.3 B.4 C.5 D.6

解析：假设有3个矿泉水空瓶，再向店主借一瓶矿泉水，喝了以后，连同原来的3个空瓶共4个空瓶换喝下去的矿泉水.本题的本质就是有3个空瓶，就能喝矿泉水一瓶，所以15个矿泉水空瓶能喝矿泉水5瓶，故选C.

二、借“体”

例2 如图1，已知该物体的左、右侧的高分别为4cm和6cm，直径为4cm，则这个物体的体积为______.

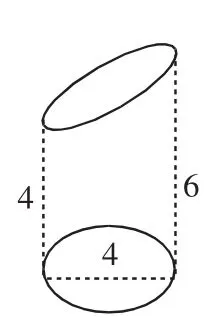
图1

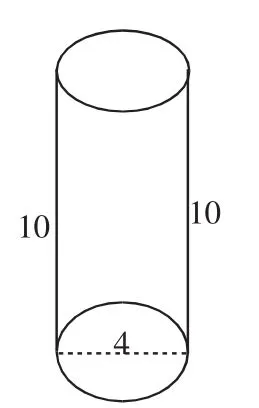
图2

解析：再“借”一个同样大小的物体，把两个拼接成一个高为10、底面直径为4的圆柱（如图2），则V圆柱=S·h=4π·10=40π.

原物体的体积等于该圆柱体的体积的一半，为20π.

三、借“数”

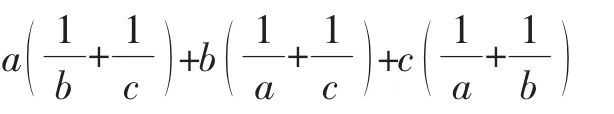
解析：借数“1”来解决问题.

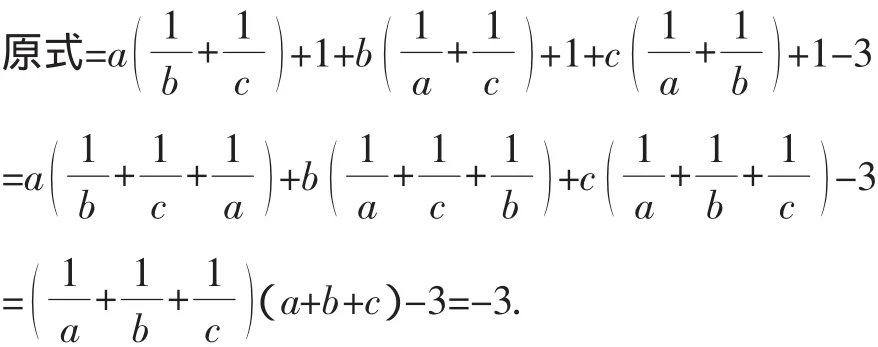
四、借“项”

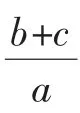
解析：b－c=（b－a）+（a－c）.

由（b－c）2－4（a－b）（c－a）=0，

得［（b－a）+（a－c）］2－4（a－b）（c－a）=0.

即（b－a）2+（a－c）2－2（a－b）（c－a）=0.

所以［（b－a）－（a－c）］2=0.

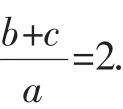
五、借“元”

曾有中考的“阅读理解题”考过下面的解方程：

解得y1=2，y2=3.

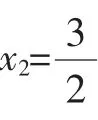
得2x=1+y=1+5，所以x=3.

经检验：x=3是原方程的解.

六、借“线段”

例6 如图3，在梯形ABCD中，AD∥EF∥GH∥BC，AE=EG=GB，AD=18，BC=32，求EF+GH的值.

解析：取AB的中点P，CD的中点Q，连接PQ.

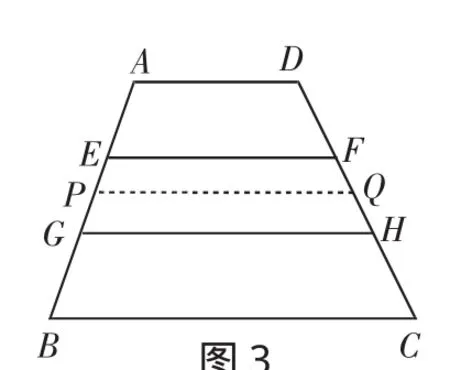
图3

根据题意，得PQ是梯形ABCD的中位线，也是梯形EGHF的中位线.

所以EF+GH=AD+BC=18+32=50.

七、借“圆”

例7 将5个相等的圆板按图4所示放置，要想一刀把它分成面积相等的两部分，应该怎样切才行？

解析：借一个等圆来解决问题：把借来的圆如图4所示摆放，然后沿图中直线一刀切就可以了.

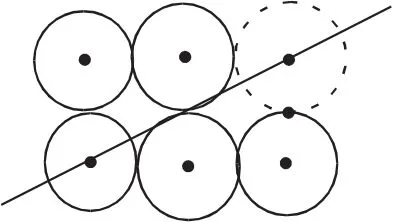
图4

八、借“公式”

例8 如图5，已知扇形OAB，点C在OA上，以O为圆心、OC为半径画弧，交OB于D，若弧AB的长为8π，弧CD的长为6π，AC=4，求阴影部分的面积.

解析：因为阴影部分的形状与梯形类似，可以借用梯形的面积公式来求阴影部分的面积.

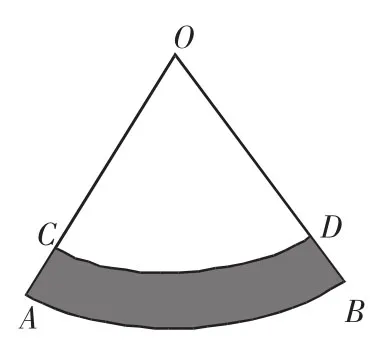
图5

九、借“图形”

数形结合是学习数学的一个极为重要的思想，很多问题借用图形来解决较为方便.

例9 （1）若方程ax2-2x+1=0（a＞0）的两根满足：x1＜1，1＜x2＜3，求a的取值范围；

（2）已知a、b均为正数，且a+b=2.求的最小值.

解析：（1）画出与方程对应的二次函数y=ax2-2x+1（a＞0）的草图（如图6）.

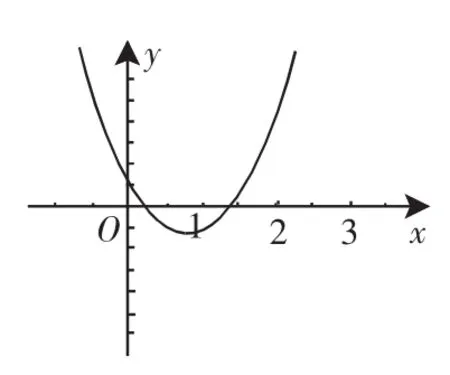
图6

由图6可知：当x=1时，y＜0；当x=3时，y＞0.

即a×12－2×1+1＜0；a×32－2×3+1＞0.

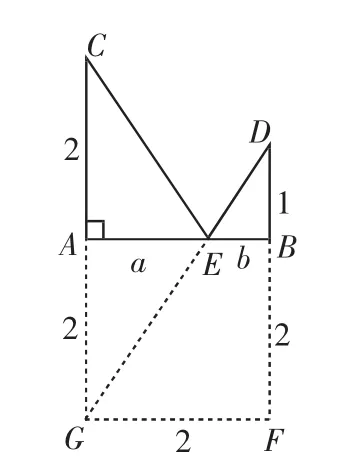
图7

（2）如图7，作线段AB=2，在AB上截取AE=a，EB=b，过A作AC⊥AB，且AC=2，过B作BD⊥AB，且BD=1.由勾股定理，得，原题即求CE+ED的最小值.

延长CA至G，使AG=AC，连接GE、DE.由三角形两边之和大于第三边，得G、E、D三点共线时，GE+ED=DG最短.作出图形，延长DB至F，使BF=AG，连接GF.

在Rt△DGF中，DF=1+2=3，GF=AB=2.

所以CE+DE的最小值是

小结：此题由式子的特点联想到勾股定理，构造图形解决问题.

十、借数学“模型”

例10 如图8，梯形ABCD中，AD∥BC，AB=CD，P为BC上任一点，PM⊥AB，PN⊥CD，BE⊥CD，垂足分别为M、N、E.求证：PM+PN=BE.

解析：我们曾经学习过一个模型：“等腰三角形底边上的任一点到两腰的距离之和等于一腰上的高”，可以借用这个模型来解决问题.

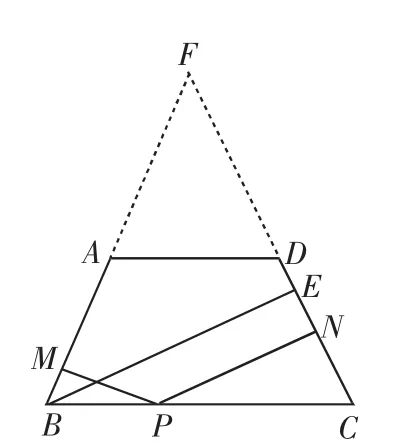
图8

延长BA、CD交于一点F.

由梯形ABCD为等腰梯形，

得∠ABC=∠C，则△FBC为等腰三角形.

所以FB=FC.

连接PF.

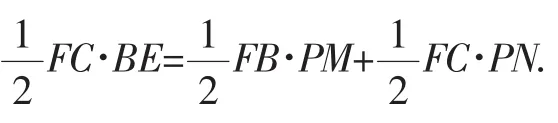
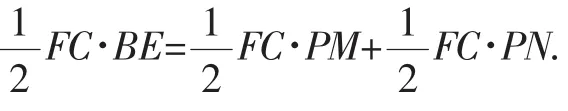
即PM+PN=BE.

运用“借”的艺术，不仅可以解决数学问题，而且能够通过“借”培养学生的知识迁移能力，对学生潜能的发展颇具意义.