薄壁管材矫直过程应变中性层偏移模型与分析

张子骞 杨会林 田永利

1.东北大学，沈阳，110004 2.天津大学，天津，300072

0 引言

近年来，高精度薄壁金属管材在工业、军事、医疗、航空航天、石油化工等领域中的需求急剧上升，为使管材具备理想的直线度和圆度，必须在出厂或使用前对其进行精整矫直。目前，薄壁管材的矫直生产一般通过人工经验或反复试矫完成，生产效率较低、产品质量稳定性较差，且针对的理论研究尚少。基于经典管材矫直理论确定的工艺参数在生产实践中，表现出矫直精度低、截面畸变，甚至无法对工件有效矫直，并不适合薄壁管材的矫直生产，因此亟待对薄壁管材的矫直机理和变形过程进行深入的理论研究。

薄壁管材的矫直是针对已弯曲的管材施加更大程度的反向弯曲来实现的，与管材弯曲理论相似，弯曲外侧和内侧之间存在一个应变中性层［1］。随着弯曲变形程度的不断增大，中性层将偏移管材中心层，对偏移量的解析及其对矫直过程影响的分析是后续深入研究薄壁管材矫直理论的基础。目前，国内外针对中性层偏移问题的处理有两种方法:一种是基于梁弯曲的工程理论，忽略中性层的偏移［2］;一种是由管材精弯理论建立的偏移模型，其理论基础为平面应变条件下平板塑性弯曲的Hill理论［3-5］。这两种方法在处理普通板材和管棒材的弯曲与矫直问题时具有较好的适用性，但不适合薄壁管材的矫直，同时这些模型对材料性能的变化不敏感。为此，本文针对薄壁管材的结构特点，确定了平面变形的应力应变关系，基于此对应变中性层的偏移量进行了解析，分析了其变化趋势和对矫直过程的影响，为深入研究薄壁管材的矫直机理和变形过程提供理论依据。

1 基本假设

在建立中性层偏移模型时需引入以下假设:

(1)材料是均质、连续及各向同性的，忽略矫直变形区的Baushinger效应，即材料具有拉压一致性，并认为应力中性层与应变中性层重合。

(2)任意垂直于中心轴的管材截面在矫直过程中始终为平面，且与中心轴保持垂直;相邻两截面间无倾斜扭曲，并忽略管材截面尺寸的变化。

(3)薄壁管材矫直变形过程中的塑性区域遵循体积不变原则。

(4)由于管壁很薄，故忽略管材矫直过程中的壁厚变化，同时径向正应力远小于其他应力，可忽略不计。

(6)矫直工作过程平稳，管材在工作辊面上做纯滚动，在矫直辊缝内的变形区可视为等弯矩纯弯曲过程［6］。

2 矫直变形分析

薄壁管材通常指管径与壁厚之比远大于20的管材，其在矫直过程中易出现起皱、扭曲和破裂等缺陷，为避免缺陷产生，通常采用减小单次反弯变形量，增加反弯次数的方法，一般采用8辊或10辊斜辊矫直机。工作辊分为上辊与下辊，在空间上交错布置于管材两侧，与被矫直管材成一定夹角，如图1所示［6］。具有初始曲率的管材依次通过中间各组具有等曲率辊形的矫直辊，进行连续弯曲变形实现矫直。

图1 上下矫直工作辊空间布置

这里采用切块法对薄壁管材在辊缝内的矫直变形区进行分析，与经典管材弯曲理论在圆柱坐标系下选取微元体的方法不同，管材在矫直时具有初始曲率，管壳表面为空间曲面，故这里选用空间子午坐标系，在辊缝内矫直变形区的任意位置取微元体单元ABCD，如图2所示。该单元体由2个夹角为dθ的管材子午面与2个夹角为dφ的平行圆包围而成，子午面与某一基准子午面夹角为θ，平行圆处的管壳表面法线与弯曲轴线夹角为φ，因管壁较薄，取微元体的厚度为管壁厚度t。同时规定任意一点的坐标方向如下:X轴方向为平行圆的切线方向，Y轴方向为管材子午线的切线方向，Z轴方向为管材外表面的法线方向。

薄壁管材的矫直变形与普通管材弯曲变形的相似之处:变形区以中性层为界，X方向外侧材料主要受切向拉伸而伸长，内侧材料主要受切向压缩而缩短。

图2 薄壁管材矫直区应力应变状态模型

薄壁管材的矫直变形与普通管材的弯曲变形也有很大不同:在Z方向上，普通管材弯曲理论认为外侧壁厚减小，内侧壁厚增大;薄壁管材因壁厚较小，矫直工艺本身要求矫直前后壁厚基本无变化，故矫直变形程度相对较小，因此矫直过程造成的厚度变化是十分微小的，由假设(4)知，Z方向上的变形可忽略不计，即εr=0;同时Z方向上的正应力远小于其他应力，有σr=0，故矫直区的三维应变状态简化为平面应变问题，则Z平面上的切应力分量 τθr=τφr=0，切应变分量 γθr=γφr=0。

薄壁管材的矫直与普通管材的弯曲的另一个重要区别是加工工艺不同。普通管材在弯曲时，沿轴线运动通过弯曲模，管材本身并不绕轴旋转，因此分析时可将管材子午线切线方向即Y方向的应力与应变忽略;薄壁管材在图1所示的空间交错的工作辊中螺旋前进，管材除了沿轴线直线运动外，还绕Y轴旋转，再者因管材厚度小，Y方向上抵御失稳的能力差，因此Y方向的应力与应变需要计入。同时，由于薄壁管材矫直变形程度相对较小，截面上横剪力τθφ虽然存在，但由假设(2)、(6)可认为τθφ是足够小量，而由横向剪应变引起的横截面任何变形可以忽略［7］，因此 τθφ=γθφ=0。

经上述分析，矫直变形区的应力应变状态与相关几何关系如图2所示。其中，r为薄壁管材半径，Rw为薄壁管材几何中心轴反弯半径，管材弯曲矫直时，沿弯曲切线方向(X向)作用的应力、应变为σθ和εθ，沿管材子午线切线方向(Y向)作用的应力、应变为σφ和εφ，弯曲应变中性层偏移角为α，t为管壁厚度。

3 矫直区弹塑性应力应变状态

3.1 应力平衡微分方程

对微元体单元ABCD列写应力平衡微分方程，在X方向上由于假设τθφ=0，因此

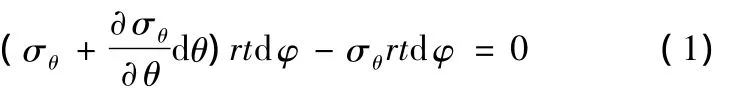
在Y方向上，考虑σφ的同时还要考虑σθ在Y方向上的投影，如图3a所示，σθ在平行圆径向的投影分量为σθrdφdθ，则该力在Y方向上的分量为 σθrdφdθcosφ，如图3b所示。因此，对Y方向列写应力平衡微分方程，有

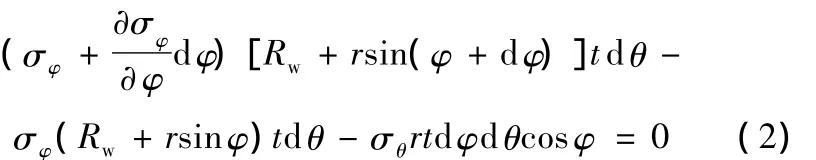
又因为 sin(φ+dφ)=sinφcosdφ+cosφsindφ ≈sinφ+dφcosφ，将其代入式(2)并化简整理得

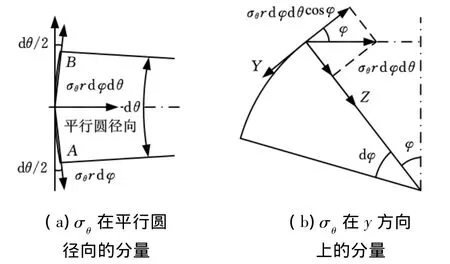
图3 σθ的投影关系图

Z方向上的正应力σr=0，因此不考虑该方向的应力平衡方程。

3.2 应变分析

薄壁管材具有初始曲率，故可假设微元体ABCD初始处于压缩区，则反弯后微元体处于拉伸区。由于管壁较薄，若想实现矫直其初始弯曲程度不能太大，可认为矫直前薄壁管材的几何中心轴与中性层重合，则管材的初始长度l0为

式中，R0为薄壁管材矫直前的初始曲率;θ0为薄壁管材矫直前的初始中心角。

微元体ABCD处初始纤维长度lφ0为

薄壁管材在矫直时需反向弯曲，中性层向弯曲轴向方向偏移α角，此时中性层的长度lw为

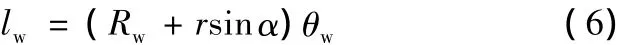
其中，θw为薄壁管材矫直时的反弯中心角，此时微元体ABCD处的纤维长度lφw为

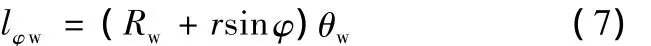
因此，Y方向的真应变为

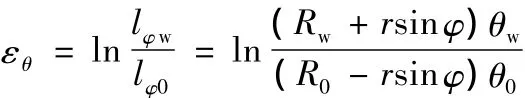
变形前后中性层的长度保持不变，矫直区的中性层长度等于管材初始长度，即

因此

3.3 弹性区应力应变关系

为使薄壁管材得到矫直而截面形状基本不变，必须保证中性层附近的某个区域为弹性变形区域。由于弹性变形区域较小，且弹性变形量通常较小，因此可认为弹性区内各变形层的初始长度均为管材的初始长度，则弹性区Y方向的真应变可近似表示为

在弹性区域中，金属遵循线弹性变形的基本原理，其本构关系遵循广义胡克定律:

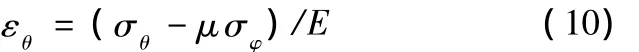
其中，μ为泊松比，将式(10)代入式(9)得

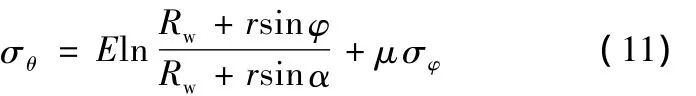
将式(11)代入式(3)并整理得

该一阶线性非齐次微分方程的通解为

将式(14)～式(16)代入式(13)并化简整理得

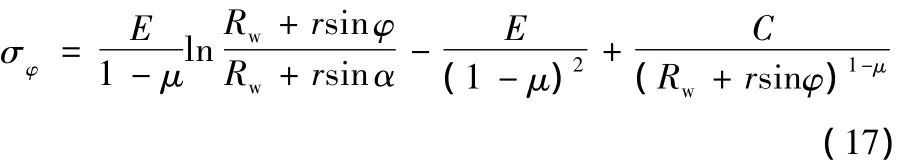
将式(17)代入式(11)并化简整理得

又由假设(1)可知，当φ=α时，σθ=0，将其代入式(18)可得

将式(19)代入式(17)、式(18)，得弹性区X、Y方向的主应力:

3.4 塑性区应力应变关系

薄壁管材在矫直过程中，除中性层附近的弹性区域外，其余均为塑性变形区域，遵循金属塑性变形相关规律。由假设(3)知，在塑性变形区有εθ+εφ=0，则 εr=(εθ+εφ)/2。平面应变状态下，由增量理论知σr=(σθ+σφ)/2。因此，塑性区的等效应力、等效应变为

由假设(5)知

塑性变形相对于弹性变形而言，变形程度较大，故Y方向塑性应变由式(8)表示。将式(8)、式(22)、式(23)代入式(24)并整理得

4 中性层偏移数学模型

薄壁管材在矫直过程中，弹性区域与塑性区域必然存在一个屈服分界面，当管材的变形量增大到一定程度，材料发生初始屈服，由假设(5)可知，弹性区的等效应力与等效应变的关系为

当弹性区外层发生初始屈服时，由Mises屈

服准则有

式中，σs为屈服应力。

将式(27)、式(26)代入式(28)得

若此时屈服面偏移中心轴的角度为β，将式(20)、式(21)代入式(29)得

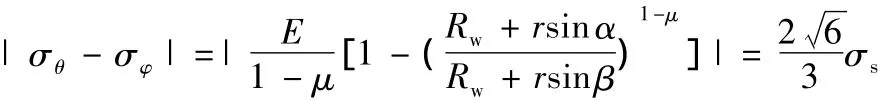
因此

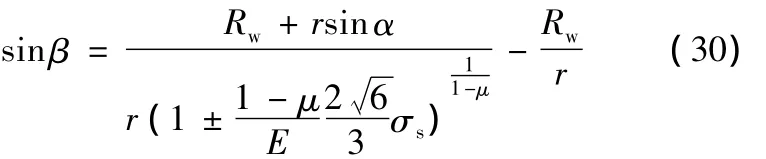
而对于塑性区的应力应变状态，在初始屈服时同样应满足式(28)，即

5 数学模型分析与仿真实验

由式(33)可见，中心层偏移角α与薄壁管材的工艺结构参数(初始相对弯曲半径R0/r、反弯相对弯曲半径Rw/r)有关。通常，矫直工艺将来料管材的R0/r最大值规定为定值，这样α便随Rw/r的变化而变化;同时，α还与材料的力学性能有关，式(33)中的量纲一参数S、T就是由材料的力学性能决定的。不同金属的力学性能与结构参数(薄壁管材半径r=20mm，管材壁厚t=1mm)如表1所示［8-9］，计算了不同Rw/r下的偏移角值，如图4的空心点所示;基于此拟合了α随Rw/r的变化曲线，如图4的实线所示。为验证偏移模型的正确性采用ANSYS/LS－DYNA对典型材料的薄壁管材矫直变形过程进行了动态仿真，测量了相同条件下的中心层偏移角，在图4中以虚线表示。

表1 不同金属力学性能与结构参数表

图4 不同典型金属材料薄壁管材α随R w/r的变化曲线

由图4可见，中心层偏移角的仿真实验值与理论计算值存在一定差距，这主要是由仿真过程未计入管材的初始变形、建立有限元模型时网格划分较大、理论计算模型并未涉及约束形式等原因造成的，但两者差距并不是很大，基本控制在5°以内，同时仿真实验值与计算值随Rw/r的变化趋势大体相同，因此可认为式(33)的计算结果近似准确。

由图4可见，在R0/r一定的前提下，中心层偏移角α随Rw/r的减小而增大，这说明当初始弯曲程度相同时，对于同一管材半径，矫直反弯半径越小，管材的变形程度越大，中性层向内偏移越大;对于同一反弯半径，管材的半径越大，中性层偏移越大，这些定性分析结果与文献［3-4］得到的结果相似。

对比图4a和图4b可知，不同材料的薄壁管材在矫直时的偏移角相差很大，这说明α与材料的力学性能有关，材料的塑性越好，偏移程度越大，这是文献［3-4］中模型所无法体现的。由图4a可见，对于碳素结构钢、合金结构钢等材料的管材，由于材料塑性变形能力相对较弱，管材初始弯曲半径较大，为防止管材在矫直过程中发生破坏，其反弯半径也相对较大，因此中性层偏移较小，一般均在2mm以内，故在分析计算时可认为中性层不发生偏移。由图4b可见，对于不锈钢、铝合金与铜合金等材料的管材，由于材料塑性变形能力相对较强，其初始弯曲半径通常较小，若想实现矫直，其反弯半径也相对较小，中性层偏移较大，故在分析计算时需考虑中性层的偏移。

上述分析仅针对普通规格薄壁管材的反弯矫直，并不适用于微小直径及超大直径薄壁管材的矫直与弹塑性弯曲。

6 结论

①本文建立的薄壁管材矫直过程的中性层偏移与相关理论模型，可对弹塑性变形区的应力应变状态、初始屈服面与应变中性层位置进行理论估算与分析。仿真实验证明，该理论模型是近似正确的，为进一步深入研究薄壁管材矫直机理和变形过程提供了理论依据。②薄壁管材矫直时，中心层的偏移量不仅与工艺结构参数有关，还与材料的力学性能有关，它随相对反弯半径的增大而减小，随金属塑性变形能力的增强而增大。③对于碳素结构钢、合金结构钢等材料的薄壁管材，矫直过程的中性层偏移量较小，在工程计算分析时可忽略不计;对于不锈钢、铝合金与铜合金等金属材料，中性层偏移量较大，分析计算时必须考虑。④本文建立的理论模型及其方法可推广应用到薄壁型钢的矫直及相关领域的分析研究中。

［1］Stechpwicz F.Bending with Upsetting of Copper Tube Elbows［J］.Journal of Materials Processing Technology，2000，100:236-240.

［2］崔甫.矫直原理与矫直机械［M］.北京:冶金工业出版社，2002.

［3］鄂大辛，郭学东，宁汝新.管材弯曲中应变中性层位移的分析［J］.机械工程学报，2009，45(3):307-310.

E Daxin，Guo Xuedong，Ning Ruxin.Analysis of Strain Neutral Layer Displacement in Tube － bending［J］.Chinese Journal of Mechanical Engineering，2009，45(3):307-310.

［4］余同希，章亮炽.塑性弯曲理论及其应用［M］.北京:科学出版社，1992.

［5］Li Longyuan，Kettle R.Nonlinear Bending Response and Buckling of Ring－stiffened Cylindrical Shells under Pure Bending［J］.International Journal of Solids and Structures，2002，39:765-781.

［6］张子骞，张柏森，杨会林，等.管棒材等曲率矫直力模型可视化设计［J］.东北大学学报(自然科学版)，2012，33(3):409-413.

Zhang Ziqian，Zhang Baisen，Yang Huilin，et al.The Visual Design on the Force Model of Tubes and Bars Equal Curvature Straightening［J］.Journal of Northeastern University(Natural Science)，2012，33(3):409-413.

［7］王俊奎，张志民.钣壳的弯曲与稳定［M］.北京:国防工业出版社，1980.

［8］成大先.机械设计手册［M］.5版.北京:化学工业出版社，2009.

［9］刘鸣放，刘胜新.金属材料力学性能手册［M］.北京:机械工业出版社，2010.