射频自动阻抗匹配的分层遗传算法实现

熊智挺，谭阳红，易如方，卢鸣凯

湖南大学 电气与信息工程学院，长沙 410082

射频自动阻抗匹配的分层遗传算法实现

熊智挺，谭阳红，易如方，卢鸣凯

湖南大学 电气与信息工程学院，长沙 410082

1 引言

射频天线阻抗匹配是射频识别中的一个重要组成部分，射频读写器在移动的过程中，天线的感应系数和阻抗都会发生变化，这种易变性会导致发射极传输功率损耗增大，降低识别能力，影响读写器的工作。当天线负载与传输线负载失配时，传输线上除了出现入射波外，还会出现反射波，反射波的存在意味着传送线终端的功率不能全部被负载所吸收，从而降低了传输效率。射频电路中的阻抗失配，不仅不利于电路低压低耗的实现，而且过高的反射系数将会减少射频元件的使用寿命，因此阻抗匹配在射频技术中有着极其重要的意义。

在工程实际中，如移动电话、蓝牙装置、车载天线等，其天线的场分布会受周围环境的影响而改变天线的阻抗值[1]，因此自动阻抗匹配技术受到了广泛研究[2]。早期由Sun.Y提出有L型自适应匹配网络[3]，但是由于其匹配区域比较小，逐渐被π型、T型和多级复合型匹配网络[4]所替代。随着匹配网络复杂度的增加，采用智能优化匹配算法也成为了必不可少的一项。通过对负载变化进行实时监控，快速地对匹配网络中各元件参数进行求解，从而实现自动阻抗匹配。也可以认为自动阻抗匹配就是数值寻优问题。常用的数值寻优算法有：粒子群算法[5]、模拟退火算法[6]、遗传算法[7]等。文献[5]采用改进的免疫粒子群法解决数值寻优问题，文献[6]采用加入模拟退火的粒子群算法进行数值优化，文献[7]综述了粒子群算法和遗传的算法对其进行了对比。然而这些算法都存在陷入局部最优的问题。因此，许多学者对预防算法陷入局部最优方面做出努力。文献[8]利用对传统遗传算法进行了改进，文献[9]对粒子群算进行了改进，但这些算法对搜索空间有着较高的要求，当算法空间达到三维及以上时，收敛速度将成指数级下降。遗传算法作为智能优化算法的一种，具有求解不依赖初始条件，及对求解域无可微或连续等较为苛刻的要求等优点。由于遗传算法中具有变异操作算子，理论上能避免了遗传算法陷入局部最优从而搜索到全局最优解。然而，变异操作是随机过程且在实际应用中每一代遗传操作变异个体在种群中的比重很低（1%～10%）。因此，遗传算法在寻优过程中容易出现早熟（即陷入局部最优）而使得收敛速度变慢。

针对单层遗传算法中的早熟和慢收敛的问题，许多改进方法被相继提出，例如：并行遗传算法[10]、多层遗传算法[11]等。并行遗传算法通过将多个遗传算法并行运行，能够有效地减少计算时间，但多个并行子程序中优良个体不能相互传递。多层遗传算法的实质为将子层算法作为个体操作，能够有效地抑制近亲繁殖，但算法的运行时间会增加。通过结合二者的优点，本文提出采用分层遗传算法来实现自动阻抗匹配，算法采用了树形结构，使子层之间具有并行特性并能够抑制近亲繁殖，修改了遗传算法中交叉操作算子，预防早熟。以π型阻抗匹配网络为例，对原算法及分层遗传算法进行了对比测试，结果表明，利用分层遗传算法实现自动匹配，得到的阻抗匹配结果精确，且很好地预防了遗传算法早熟现象，收敛速度得到了较大的提升。

2 匹配网络分析

在射频电路中，为了实现天线阻抗和源级之间的匹配，往往在源级和负载之间加入无源匹配网络。如图1所示，当负载天线阻抗发生改变时，传感器将负载的相关信息（负载端的阻抗值、反射系数或VSWR）传输给控制单元，控制单元利用从传感器所获得的信息经过其内部的控制算法得到匹配网络各元件优化参数，通过作用单元对网络各参数进行动态调整以实现信号源与负载天线自动匹配。

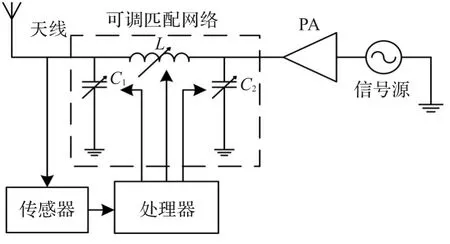
图1 自动阻抗匹配网络

对π型阻抗匹配网络进行电路分析，如图2所示，射频发射机被等效为电压源Us与电源内阻Rs串联的形式，射频天线则被等效为负载ZL。在电源与负载间由C1、C2和L所构成的电路就是π型无源匹配网络。C1、C2和L是可调电容和电感，通过调节三个参数的值，来实现 Rs与Zin共轭匹配。

图2 匹配网络电路

通过计算，可以得到：

其中ω表示是电路工作频率，Zin表示的是匹配网络与负载所等效电路的输入阻抗，Uin表示的是等效阻抗Zin两端的电压，Iin表示的是流过等效阻抗Zin的电流，Г和VSWR分别表示的是负载的反射系数及电压驻波比。

3 分层遗传算法

3.1 算法设计

为了抑制早熟，本文引入分层机制来改进遗传算法。单层的遗传算法仅在一个种群内部进行遗传操作，并不适合自然界多种群的竞争方式，容易出现早熟现象。以人类为例，在人类进化的早期由于地理环境的阻隔，人种之间的进化是相互独立的。并且由于各自所处的环境的不同，各人种都朝着更适应各自生存环境的方向进化。可当进化到了一定时期，地理环境的阻隔被打破，进化不再是相互独立过程而是个形成一个各种群相融合的大种群继续进化。

本文提出的分层机制模拟的是上述人类进化过程：（1）初始化几个种群规模较小的种群；（2）每个种群选取不同的遗传算法参数进行独立的进化；（3）当各种群独立进化到一定代数后，将进化后的各种群合起来构成一个更大规模的种群，然后再将这一种群作为初始种群进行进化。另外对于过程（1），本文是在问题域内先随机生成一个规模很大的种群，然后再在这一种群中选择适应值较大的个体作为过程（1）中各小种群的初始种群。这样会有利于遗传算法的收敛。算法流程如图3所示。

3.2 各层遗传算法

对于图3中各个子遗传算法，为了获得精确的匹配参数，本文采用的是浮点遗传算法（floating-point Genetic Algorithm）。浮点遗传算法采用的是实数编码方式，与传统采用二进制编码方式的遗传算法相比，该算法不仅省去了复杂的编码译码过程而且由于不受编码位数的限制求解结果也更加精确[12]。两种编码方式比较如图4所示。

图3 分层遗传算法流程图

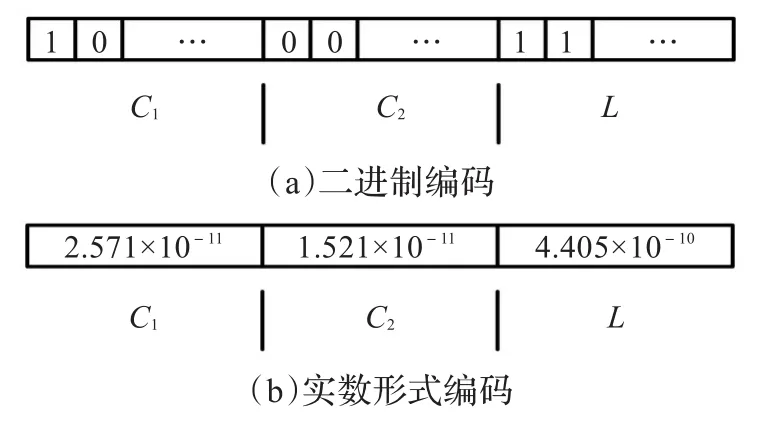
图4 两种编码方式

图4中，二进制编码方式的遗传算法，将C1、C2和L的值转换为对应的二进制编码基因，并将这些基因合成一条染色体构成个体。在个体“进化”过程中，不仅选择算子在计算个体的适应值时需要进行反复译码编码，加大了算法复杂度；而且相应的交叉及变异算子多为位操作，程序编写繁琐。实数编码方式的遗传算法，将C1、C2和L的值构成一个行向量，不仅进行选择操作时减少了反复编码译码过程，而且其交叉和变异算子为向量运算，在程序中容易实现。

3.3 选择算子实现

选择算子的作用是用来模拟自然界生物优胜劣汰的过程，即通过选择算子按概率选择出种群中适应值较高的个体遗传到下一代，而适应值较低的个体将被淘汰。算法采用排序选择机制：在每一代中，将种群中的个体按适应值从高到低进行排序，第i个个体的选择为：

其中r=q/(1-(1-q)n)，n为种群规模，q为选择压力，q∈(0，1)。

3.4 交叉算子实现

交叉算子的作用是用来模拟生物在繁衍过程中父代的基因进行交叉形成子代个体的过程。对于种群中要进行交叉操作的父代个体x1和 x2，如果它们都不是局部最优值则在二者之间适应值较大个体的领域内一定存在适应值更大的个体。经典的交叉算子就是利用了这一点来生成后代x3。

其中x2的适应值不低于 x1的适应值，而a是区间(-1，1)的一个随机数。

在遗传算法中，交叉算子的作用是使种群朝着有利于适应值增大的方向进化，即指示种群所需的正确的进化方向，因而交叉操作在遗传算法中起着决定性的作用。式（7）中的交叉算子容易使遗传算法在实际问题的求解中陷入局部最优。例如：当x1=x2时（这在实际情况中完全存在的，若选择压力q设置得较大，或是进化到后期种群趋于一个很小的区域），x2-x1=0，x1=x2=x3。因此种群将得不到进化而停滞，遗传算法陷入了局部最优，或是导致收敛步数大大增加。虽然遗传算法存在变异算子，能够使算法收敛于全局最优解，但是变异的方向是不确定的，且变异操作与交叉操作相比在遗传算法中操作次数要小得多，从而使收敛步数将成倍地增加。

本文对交叉算子进行以下修改：（1）在进行交叉操作之前，先对被选取的两个父代个体进行判断，如果被选中的父代个体相同，则在父代个体的领域内随机生成一个新的父代个体，代替一个父代个体，从而提供一个进化方向。（2）对于交叉操作中两个父代个体的选取，在经典算法中为随机选取，即种群中各个体获得繁衍下一代的权利是平等的。然而生物界中物种种群个体获得繁衍下一代的权利是不相同的，占统治地位的最优个体更容易获得繁衍的权利。因此在选择父代个体时，将经典算法中随机选取修改为选取种群中适应值最大的个体为父代个体，再随机选择另一个父代个体。这样就模拟了生物最优个体在繁衍过程中占统治地位这一现象。（3）借鉴粒子群优化算法（PSO）中个体在进化过程中，始终是向着种群中好个体的方向进化这一思想。对式（7）修改为：

3.5 变异算子实现

变异算子的作用是模拟生物在繁衍过程中个体基因发生变异的过程。基因变异体现的是生物在演化过程中的偶然性，变异的方向是不可知的，因此这里采用的变异算子为在搜索空间中生成随机的点来形成种群中的个体。

4 实验结果及对比

本文给出了几个实例来证实分层遗传算法在自动阻抗匹配中应用是成功而有效的，并与传统遗传算法进行了对比。

例1工作频率为2.4 GHz，电源电压Us为1 V，内阻Rs为50 Ω，天线阻抗ZL为25－50i Ω，传统遗传算法与分层遗传算法（均采用实数编码方式）两种算法实验的收敛对比，如图5、6所示。

图5所示，传统遗传算法适应值进化曲线一般在1 500～2 000代之内完成收敛，而相比传统的遗传算法，图6所给出的分层遗传算法进化曲线一般在50代之内即可完成收敛，将收敛代数减少了1 000代以上。实验结果说明，分层遗传算法能够有效减少收敛代数，加快运算速度。

例2在不同的工作频率，变化的天线负载阻抗下，传统遗传算法与分层遗传算法详细参数对比如表1。

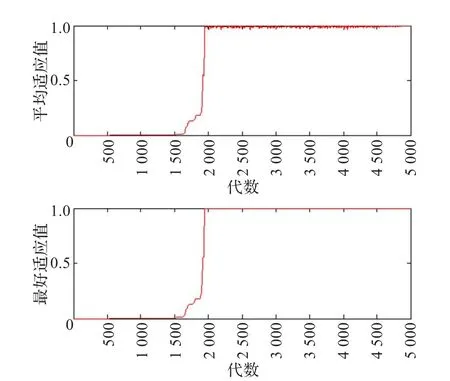
图5 传统遗传算法适应值进化曲线

图6 分层遗传算法母种群适应值进化曲线

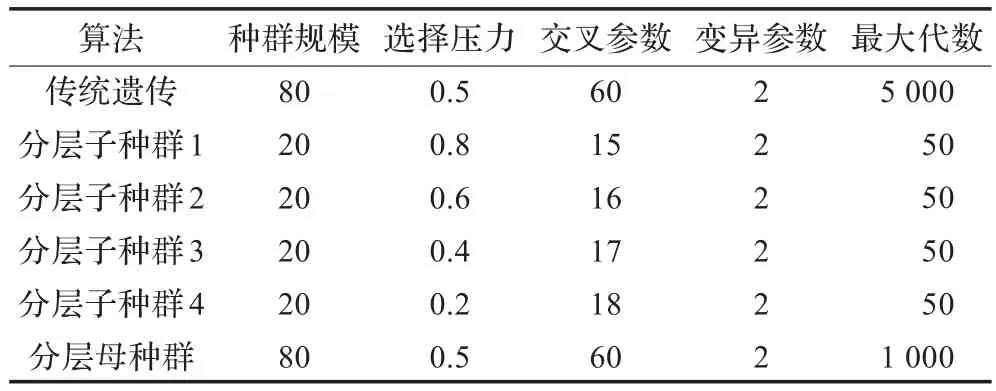
表1 算法参数设置

从表2可以看出，遗传算法很容易出现早熟现象，即算法迭代到终止进化代数时，实际匹配结果和理想值之间误差较大，算法陷入了局部最优。从表3可以出，分层遗传算法只有在频率为1.8 GHz，负载阻抗为200 Ω的情况下误差较大，出现早熟现象。算法收敛速度也也得到了较大的提升。对表2和表3进行比较可知，分层遗传算法的迭代次数较遗传算法大幅减少，这说明收敛速度得到了较大的提升；并且分层遗传算法只有在频率为1.8 GHz，负载阻抗为200 Ω的情况下才出现匹配出实际的值离理想值较远，即出现了早熟，而遗传算法则很容易出现早熟现象。这说明了分层遗传算法很好地预防了早熟现象。

通过表2和表3的匹配结果可以看出，传统的遗传算法在对天线阻抗匹配的效果上并不理想，Zin的实部误差平均在1E－1数量级上，而Zin的虚部误差平均在1E－5数量级上；而同比的分层遗传算法Zin的实部误差平均为1E－5，Zin的虚部误差平均仍为1E－5，由此看出分层遗传算法能够得到比较精确的匹配结果。而负载功率能够直观地看出匹配结果，理想匹配为5E－3 W，通过表2、3数据可以看出，传统的遗传算法一般达不到理想的匹配，随着负载的改变，效果波动比较大，与此相比，分层遗传算法在负载的波动和变化的情况下，仍然可以将负载功率保持在理想值，即使是负载阻抗为200 Ω时，算法仍然能维持较高的精度。电压驻波比VSWR和负载功率一样，证实了分层遗传算法在天线阻抗匹配方面远超传统遗传算法的优势。

表2 传统遗传算法的匹配结果

表3 分层遗传算法的匹配结果

5 总结

本文针对利用遗传算法进行射频电路自动匹配易出现早熟现象，提出采用分层遗传算法来解决自动匹配问题，从而很好地预防了早熟现象；并对遗传算法中的交叉算子进行了改进，从而提升了算法的收敛速度。通过实验结果表明，分层遗传算法较原算法求解精度高，收敛速度快，不易陷入早熟，能很好地解决射频电路自动阻抗匹配问题。由于本文电路分析过程中，认为各元件都是理想元件，因此，考虑元件的实际特征以及其寄生和分布参数对匹配结果的影响是下一步的工作。

[1]Boyle K R，Yuan Y，Ligthart L P.Analysis of mobile phone antennaimpedancevariationswith userproximity[J].IEEE Transactions on Antennas and Propagation，2007，55：1942-1948.

[2]刘汉斐，程健，钱玉良.一种自动阻抗匹配算法[J].计算机工程，2009，35（9）：275-279.

[3]Sun Y，FidlerJK.Practicalconsiderationsofimpedance matching network design[C]//6th InternationalConference on HF Radio Systems and Techniques，1994：229-233.

[4]黄秋元，董诗波.射频电路中匹配网络的设计和分析[J].武汉理工大学学报：交通科学与工程版，2007，31（6）：1061-1063.

[5]高鹰，谢胜利.免疫粒子群优化算法[J].计算机工程与应用，2004，40（6）：4-6.

[6]高鹰，谢胜利.基于模拟退火的粒子群优化算法[J].计算机工程与应用，2004，40（1）：47-49.

[7]雷秀娟，史忠科，孙瑰琪.基于遗传算子的粒子群优化算法的比较分析[J].计算机工程与应用，2008，44（14）：65-67.

[8]金晶，苏勇.一种改进的自适应遗传算法[J].计算机工程与应用，2005，41（18）：64-69.

[9]熊智挺，谭阳红，易如方，等.一种并行的自适应量子粒子群算法[J].计算机系统应用，2011，20（8）：47-51.

[10]杨昭龙，杨松林.分层并行遗传算法和遗传复合形算法及其应用[J].计算机工程与应用，2009，45（13）：203-206.

[11]Li Q S，Liu D K，Leung A Y T，et al.A multilevel genetic algorithm for the optimum design of structural control systems[J].International Journal for Numerical Methods in Engineering，2002，55：817-834.

[12]韩瑞峰，张永奎.一种改进的实数编码遗传算法[J].计算机工程与应用，2002，38（13）：78-80.

XIONG Zhiting,TAN Yanghong,YI Rufang,LU Mingkai

College of Electrical and Information Engineering,Hunan University,Changsha 410082,China

Matching impedance is very important to design RF antenna circuits.Optimized impedance is beneficial to realize low voltage and low power antenna circuits,and lower reflection coefficient will ensure that the antenna system can be running smoothly and reliably too.To avoid slow and premature convergence,it proposes a layered process technique and performs reformation including improving crossover operation.It runs the program on the MATLAB simulation platform with different loads at different frequencies and analyzes results in different conditions.These results indicate that the reformative GA can escape from premature convergence and it gets solutions whose errors are lower than predefined errors more speedy than the conventional GA.

multilevel genetic algorithm;radio frequency;impedance match;premature

阻抗匹配问题在射频技术中有着极其重要的意义，良好的阻抗匹配不仅有利于电路的低压低耗实现，而且较小的反射系数为系统的可靠运行提供了保证。针对遗传算法在自动阻抗匹配过程中收敛速度慢且易陷入早熟（即陷入局部最优），提出利用分层机制来预防早熟，并对遗传算法中的交叉操作算子进行了改进来加快收敛。通过MATLAB对上述算法进行实现，并采用不同频率及不同负载阻抗对上述算法及遗传算法进行测试从而进行比较。结果表明分层遗传算法很好地预防了早熟，收敛速度比原算法得到较大的提升。

分层遗传算法；射频；阻抗匹配；早熟

A

TP18

10.3778/j.issn.1002-8331.1202-0337

XIONG Zhiting,TAN Yanghong,YI Rufang,et al.RF impedance automatic-matching with multilevel genetic arithmetic. Computer Engineering and Applications,2013,49（23）：261-265.

国家自然科学基金（No.60876022）；湖南省自然科学基金（No.07JJ6132）；国家高技术研究发展计划（863）（No.2006AA04A104）。

熊智挺（1986—），男，硕士研究生，主要从事群智能算法、神经网络、RFID、电力系统负荷预测等方向的研究；谭阳红（1971—），女，教授，博士研究生导师，主要研究方向为RFID、自动测试与故障诊断、高速集成电路、智能与实时信息处理；易如方（1986—），男，硕士研究生，主要从事电工理论与新技术方向的研究；卢鸣凯（1989—），男，硕士研究生，主要从事智能算法与故障诊断等方向的研究。

2012-02-20

2012-05-28

1002-8331（2013）23-0261-05

CNKI出版日期：2012-06-15 http://www.cnki.net/kcms/detail/11.2127.TP.20120615.1726.023.html