用算子定义的一类特殊解析函数
2013-07-22何涛李书海
何涛,李书海
(赤峰学院数学与统计学院,内蒙古赤峰024000)
用算子定义的一类特殊解析函数
何涛,李书海
(赤峰学院数学与统计学院,内蒙古赤峰024000)
本文引进并研究一类用微分算子定义的解析函数.用最大模原理和从属关系证明该类中函数的系数不等式,然后用此定理证明类中函数的积分算子、单叶半径、凸半径和极值点等性质.
解析函数;单叶;最大模;算子;半径
1 引言
设-1≤B<A≤1,0≤α<1,β≥0,f(z)∈T,函数f(z)∈Tσ,k(α, β)当且仅当
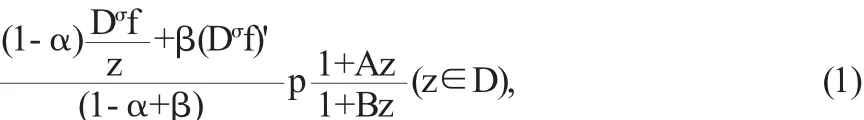
其中Dσf为[1]中引进的Salagean算子,且具有如下展开式
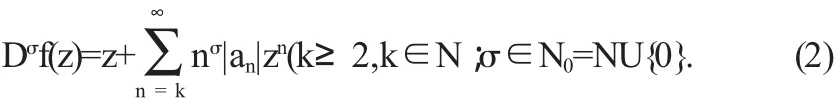
利用从属关系可知,当且仅当存在D内满足条件
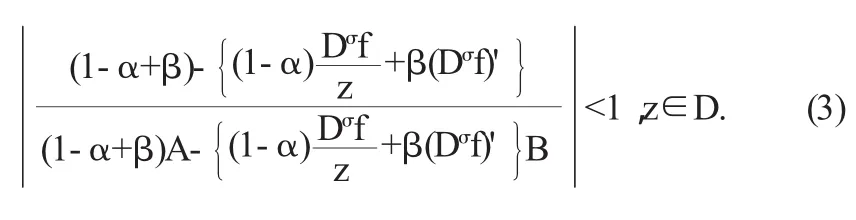
本文中讨论函数类Tσ,k(α,β)的系数不等式、积分算子、单叶半径、凸半径和极值点等性质.
2 主要结果及其证明
定理1(系数不等式)设0≤B<A≤1,0≤α<1,β≥0,函数f(z)∈Tσ,k(α,β)当且仅当
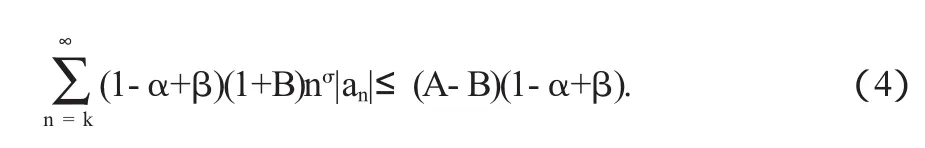
证明充分性,令|z|=1,则
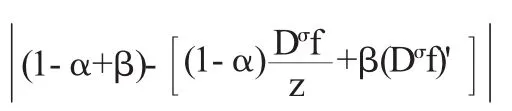
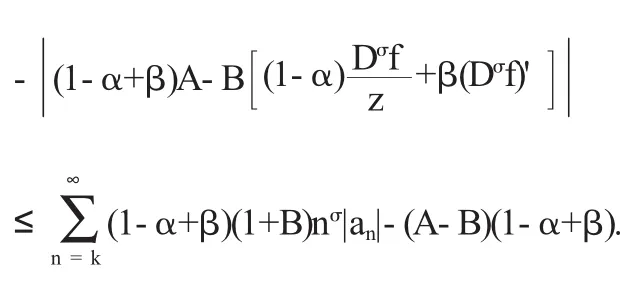
于是,由最大模原理,f(z)∈Tσ,k(α,β);必要性设f(z)∈Tσ,k(α,β),那么
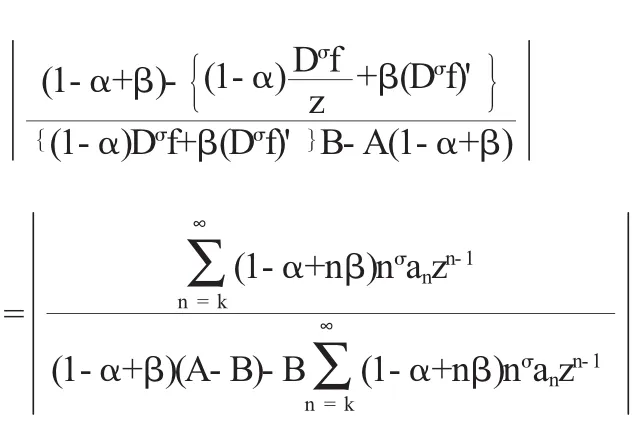
|Rez|≤z对于所有的z成立,所以,我们有
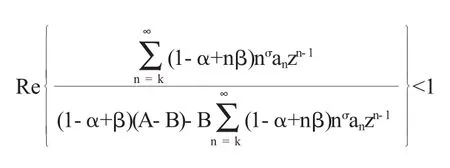
推论函数f(z)∈Tσ,k(α,β),则
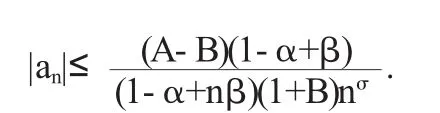
定理2(积分算子)设c是实数且c>-1 f(z)∈Tσ,k(α, β),则函数
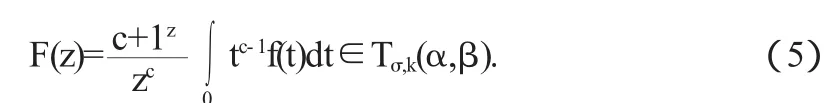
证明因为f(z)∈Tσ,k(α,β),则由F(z)的表达式,得到
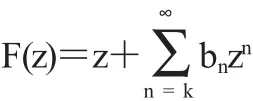
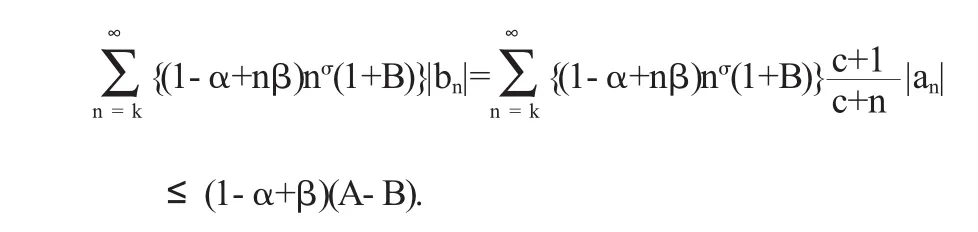
因此,F(z)∈Tσ,k(α,β).证毕.
定理3(单叶半径)设c是实数且c>-1又设F(z)∈Tσ,k(α,β),则由(5)式定义的函数f(z)在|z|<R*中是单叶的,其中
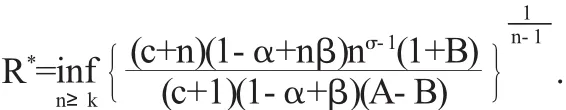
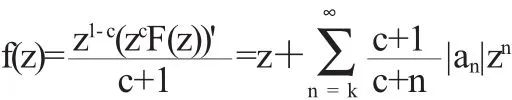
为证明f(z)在|z|<R*中单叶,只需证明在|z|<R*中有|f' (z)-1|≤1.
由定理1可知
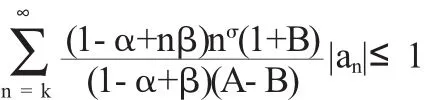
因此,如果
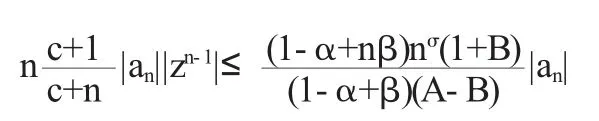
或者
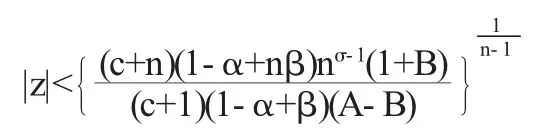
即f(z)在|z|<R*中单叶.
相同的方法容易证明凸半径:
定理4(凸半径)设f(z)∈Tσ,k(α,β),则f(z)在|z|<R中是凸的,
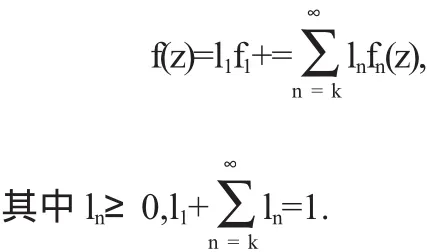
证明设
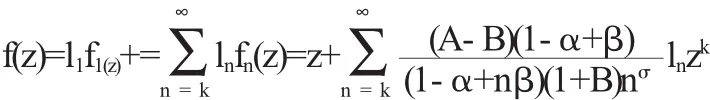
则利用定理1,我们有

〔1〕G.S.Salagean,Subclasses of Univalent Functions[J]. Lecture Notes in Mathematics,vol.1013,Springer-Verlag,Berlin,1983,pp.362_372.
〔2〕李书海.特殊解析函数[M].内蒙古科技出版社,2007.
O174
A
1673-260X(2013)07-0005-02
