基于SVD降噪和谱峭度的滚动轴承故障诊断

孟智慧，王昌

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

通常情况，轴承运行环境都比较复杂，利用加速度传感器采集的振动信号一般都包含强烈的噪声干扰，如何从信号中有效提取故障特征信息是滚动轴承故障诊断技术的关键[1]。在轴承故障诊断技术中，包络解调是最常用的方法之一，然而通常情况都要求先对振动信号进行带通滤波处理，如何设置滤波器的中心频率和带宽对信号处理的结果有很大影响[2]。谱峭度作为近几年提出的信号指标，可以有效地对带通滤波器参数做最佳选择[3-4]。

奇异值分解[5](Singular value decomposition,SVD)在信号处理中主要用于信号的降噪和周期成分的提取[6]。在信号降噪处理中，如何选择奇异值个数很关键，奇异值差分谱的最大突变点可以实现有效奇异值个数的准确判断[7-8]。因此，将SVD差分谱降噪与谱峭度结合，以应用于轴承故障诊断中。

1 奇异值差分谱降噪

实矩阵A∈Rm×n, 不论其行列是否相关，必定存在一对正交矩阵U=(u1,u2,…,um)∈Rm×m和V=(v1,v2,…,vn)∈Rn×n,使得

A=USVT，

(1)

式中：S=(diag(σ1,σ2,…，σq)，0)或者其转置，其取决于mn。A∈Sm×n,0代表零矩阵，q=min(m,n),σ1≥σ2≥…≥σq≥0,称为矩阵A的奇异值。

要对信号进行奇异值分解，需要先将信号构造成矩阵的形式，一般将信号构造为Hankel矩阵时降噪效果最好，离散数字信号X=(y(1),y(2),…,y(N)) 构造形式为

(2)

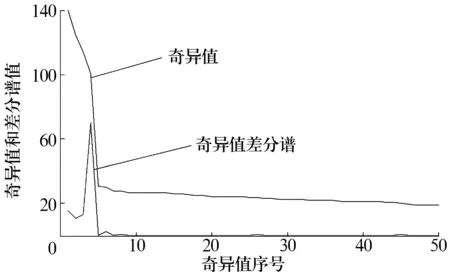
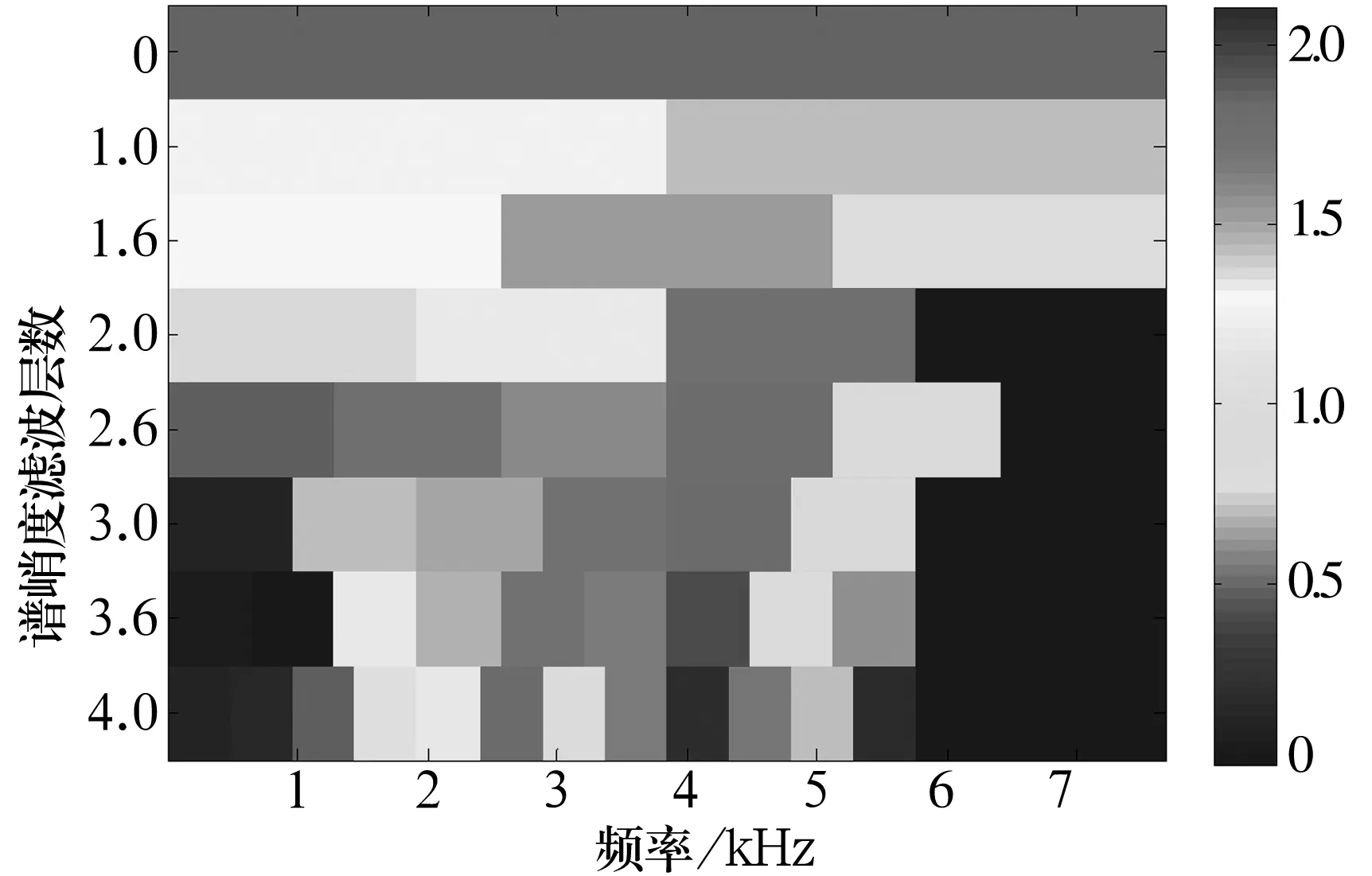
式中：1

对于SVD分解后的奇异值，按照从大到小顺序形成的序列为S=σ1,σ2,…，σq。

令

bi=σi-σi+1，i=1,2,…,q-1，

(3)

则bi组成的序列称为奇异值的差分谱，含噪信号构造的Hankel 矩阵奇异值分解后，后面的q-k个奇异值明显小于前k个奇异值，也就是说奇异值在第k个点发生突变，而前k个奇异值代表了要提取的理想信号。由于每一个奇异值对应着一个分量信号，因此，只要选择前面k个分量进行简单的叠加，就可获得降低了噪声的信号，而差分谱就可以有效的自动判断最大突变点bk。

为了验证SVD差分谱降噪效果，构造仿真信号y=sin 3t+sin 8t，采样频率为128 Hz,采样点数为512，叠加信噪比为1.073的Gauss白噪声，其波形如图1所示。

图1 原始信号波形

将信号构造为Hankel矩阵进行奇异值分解，奇异值曲线和奇异值差分谱如图2所示。由于奇异值差分谱曲线的最大突变点在前段部分，后面都趋于0。故只绘出前50个点的曲线。可以清楚的看到在第4个点出现了突变，故保留前4个奇异值，其余的置为0进行SVD重构，得到降噪后的信号波形如图3所示。降噪后波形与理想信号的误差非常小，说明利用奇异值差分谱可以对含噪信号进行有效降噪。

图2 奇异值差分谱曲线

图3 奇异值差分谱降噪后波形

2 谱峭度

为解决信号中瞬态成分无法利用功率谱检测和提取的问题，Dwyer提出谱峭度(Spectral Kurtosis, SK)的概念，文献[8]对谱峭度进行了规范化，并提出基于滤波带的谱峭度快速算法。谱峭度定义为能量归一化的四阶谱累积量，用来度量一个过程在某一频率上的概率密度函数的峰值大小。谱峭度从信号处理角度可以解释为：理想的滤波器组的输出在频率上计算得到的谱峭度值。所以谱峭度对信号中的瞬态成分敏感性更高，而且可以精确的找到所对应的频率，因此，谱峭度在检测瞬态信号成分方面有一定的优势。

非平稳情况下，定义信号X(t)的激励响应Y(t)表达式为

(4)

式中：H(t,f)为系统的传递函数，表示Y(t)在f处的复包络。

过程Y(t)四阶谱累积量定义为

(5)

S(f)为谱瞬时矩，定义为

(6)

即可得到谱峭度的定义

(7)

对于轴承故障诊断，传感器所采集的振动信号都含有强烈的加性噪声，则混有加性噪声n(t)的振动信号的谱峭度为[4]

(8)

式中：ρ(f)为信噪比。

3 故障信号分析

试验系统由轴承试验台、压电式加速度传感器(627A61型)、数据采集仪(MI6008型)、笔记本电脑组成。故障试验台如图4所示，将正常和有故障轴承依次安装在轴承试验台上，进行试验数据采集，将采集到的数据传输到电脑中进行数据处理分析。

图4 故障试验台

试验轴承型号为6307，电动机转速为1 496 r/min，采样频率为15 360 Hz，采样点数为4 096。利用线切割技术在轴承外圈加工一条宽0.5 mm,深0.5 mm的槽模拟裂纹故障，将故障轴承安装在试验台末端轴承座上，加速度传感器垂直安装在末端轴承座上。经计算，轴承外圈的特征频率为76.728 Hz。

外圈裂纹故障振动信号的时域波形及幅值谱如图5所示，可以看出信号中有一定的冲击成分，但根据波形及频谱无法有效识别故障。故将振动信号构造为Hankel矩阵进行奇异值分解，奇异值差分谱曲线如图6所示。

图5 滚动轴承外圈裂纹故障信号波形及频谱

图6 奇异值差分谱曲线

根据奇异值差分谱，保留前4个奇异值，将其余奇异值置为0进行SVD重构，则奇异值差分谱降噪后的信号如图7所示，信号呈现较好的周期性冲击。进一步利用谱峭度求得其快速峭度图如图8所示，最大峭度值出现在第4层，中心频率为4 080 Hz，带宽为480 Hz，按此滤波器参数对降噪后信号进行带通滤波并求其包络解调谱如图9所示。所对应的频率成分与滚动轴承外圈特征频率76.728 Hz及其倍频非常接近，即可判断轴承出现外圈故障，与模拟故障相符。

图7 SVD差分谱降噪信号波形

图8 降噪信号的快速峭度图

图9 最大峭度值滤波信号包络解调谱

4 结束语

利用SVD可以对含噪振动信号进行有效降噪，而差分谱在降噪时可以自动确定SVD重构时有效奇异值的个数。根据谱峭度的快速峭度图可以自动确定带通滤波器的最佳带宽和中心频率，从而实现对信号的最佳带通滤波处理。将SVD差分谱和谱峭度结合，利用轴承试验台模拟的故障信号进行了验证，该方法可有效提取轴承故障特征信息。