一种公开可验证的安全电子彩票协议

孙培勇，刘忆宁，李亚军

桂林电子科技大学 数学与计算科学学院，广西 桂林 541004

一种公开可验证的安全电子彩票协议

孙培勇，刘忆宁，李亚军

桂林电子科技大学 数学与计算科学学院，广西 桂林 541004

1 引言

由于网络方便高效的特点，其应用范围越来越广泛，人们也设想用电子彩票代替传统彩票[1-2]，使其具有更广泛的参与性。1998年，Goldschlag和Stubblebine提出了一种应用延迟函数来实现可验证的电子彩票方案[3]，并指出电子彩票方案应该满足以下三个性质：（1）公平性，每一张彩票都有相同的获奖机会；（2）公开可验证，结束后每个人都可以计算获奖数字，并且可以验证彩票的真实性；（3）封闭性，获奖数字的产生仅依赖于所销售的彩票数据而定，而不依赖可信任第三方所提供的信息。

2009年，Lee与Chang提出了t-out-of-n的电子彩票方案[4]，随后Gray和Sheedy分析指出Lee-Chang方案存在安全漏洞[5]，但是并没有给出一个系统的解决方案。他们希望能够有一种可公开验证，并且不需要可信任第三方的电子彩票方案。安全多方计算作为密码学上一种重要的方法[6]，应用十分广泛，尤其在密钥共享方面经常使用[7-9]。本文给出的安全电子彩票协议，基于安全多方计算的原理实现对随机函数及获奖数字公正性的验证，其过程不需要可信任第三方的参与。

2 Lee-Chang方案

Lee-Chang电子彩票的参与者主要包括：彩票发行者（LA）、购买者（Player）、认证中心（CA）和银行（B）；方案包括准备阶段、销售阶段、摇奖阶段、领奖阶段。

2.1 准备阶段

步骤1LA在公告板上公布n个彩票数字，a1，a2，…，an，并选取n个互素的数，d1，d2，…，dn，其中di＞ai，i=1，2，…，n。

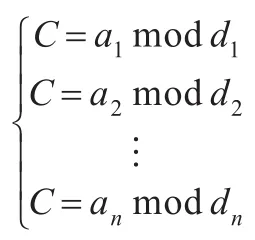
步骤3LA计算，其中(e，N)是LA的公钥，N是两个大素数的乘积，ed=1modϕ(N)。LA公布(a1，D1)，(a2，D2)，…，(an，Dn)。

2.2 销售阶段

Alice通过以下步骤购买彩票：

步骤1Alice从(ai，Di)(i=1，2，…，n)中选取t对，记为(a′j，D′j)，j=1，2，…，t。

步骤2对于(′)，Alice选取随机数rj，计算，以及PKLA(α1,α2,…,αt,rA1,rA2,Ecash)，其中PKLA是用LA的公钥进行加密的算法，rA1，rA2是随机数。Alice将PKLA(α1，α2，…，αt，rA1，rA2，Ecash)发送给LA。

步骤3LA收到Alice的消息后解密，并检查Ecash是否有效。如果有效，LA对收到的消息进行签名，即

步骤4LA计算Countf=Countf-1+rA1mod f，其中f是至今已经售出的彩票的张数。然后，LA在公告板上公布(Countf，f)，并且生成。最后，LA将彩票发送给Alice。 (kf，Countf，f)保存在LA的数据库中，Kf是LA和Alice之间的对称密钥。

步骤5Alice收到彩票后解密，并对比所得到的Countf与公告板上是否一致。

2.3 摇奖阶段

假设最后结果得到Countf=Cr，购票时间结束后，LA按下述步骤摇奖：

步骤1首先计算w=Countfmodn，其中n是彩票数字的个数。

步骤2LA然后将种子w输入随机函数得到CW，Ran(w)=CW={cw1，cw2，…，cwt}。

步骤3LA公布获奖号码结果CW。

2.4 领奖阶段

假设Alice所选取的t个数字与CW相等，成为中奖者，她需要提交证据证明自己是获奖者。

步骤1Alice发送给LA。

步骤2LA计算从而得到LTf和，LA根据(Countf，f)找到密钥kf，解密LTf。

步骤3LA用解密盲签名β1,β2,…,βt，得到{d′1,d′2,…,d′t}，并计算

如果{b1，b2，…，bt}和CW相同，LA确信Alice是获奖者。

Lee-Chang方案漏洞分析：

（1）由2.3节摇奖阶段可知，种子w是由Countf模n得到的，因此中奖号码Ran(w)=CW={cw1，cw2，…，cwt}最多有n种可能性，即Ran(0)，Ran(1)，…，Ran(n-1)。而n是彩票数字的个数，所以当n比较小时，购买者就可以通过购买所有可能中奖号码Ran(0)，Ran(1)，…，Ran(n-1)，这样必然有一张会中奖。例如当n=100时，购买者就可以购买100张彩票，数字分别为Ran(0)，Ran(1)，…，Ran(99)，这样就保证了自己中奖。

（2）最后一个购买者E可以与LA合谋预测w，从而预测中奖号码，然后购买。假设平均购买1张票的时间为t，购买终止时间为Tp。在(Tp-t)时刻时（即平均只能够卖出1张票时），设此时已经卖出f-1张票，E和LA进行如下攻击：LA负责干预此时其他购票者不能购票成功（例如通过拖延计算等手段），E用事前已经准备好的，计算然后E按照进行购票，并且在购票阶段的步骤2中，向LA传递的数据中令rA1=。从而保证了Countf=， w=′，最终有中奖号码

（3）对于中奖者的合法性，除了LA之外其他人无法验证，而且在领奖阶段只有LA与中奖者两人参与，使得LA有可能与其中一个购票者合谋作弊。假设LA与购买者A合谋，从购票阶段可知，其他人知道关于A的信息只有公告板上公布的(CountfA，fA)。而(CountfA，fA)的值与A购买彩票时选择的数字无关，只与购票阶段选择的随机数rA1和购票的次序有关。因此，当A原来购买的票没有中奖时，LA和A可以合谋将A原来选择的彩票数字修改为中奖号码，但是rA1和fA不变，并由LA签名，此时其他人不能从公告板上的(CountfA，fA)判断出A的票已经修改。并且中奖号码不会因为A选择的彩票数字改变而改变，因为种子w只与A的CountfA有关，与A选择的彩票数字无关。

3 具有可验证公平性的n中选t的安全电子彩票方案

本文新的方案仍分四个阶段：准备阶段、销售阶段、摇奖阶段、领奖阶段。Lee-Chang方案中原有的符号及标记在下文中仍沿用，增加新的符号：计算中心（CC，仅承担计算功能，不具有可信任第三方的职责）。

3.1 准备阶段

CC公布彩票数字所在的范围域Zp（p为素数）。

3.2 销售阶段

步骤1Alice选取两个大素数pi和qi，并计算Ni=piqi，将(ei，Ni)和di分别作为自己的公钥和私钥。

步骤2Alice选择t个数bi1，bi2，…，bit∈Zn作为自己所买彩票的数字，记为Ai={bi1，bi2，…，bit}。

步骤3Alice计算，并计算hi=Hash(IDi||Ai)，其中ei和IDi分别是Alice的公钥和身份信息。

步骤4Alice将(，hi，ei)发送给计算中心CC。

步骤5CC收到(，hi，ei)后，进行数字签名Li= sign(Aeii，hi，ei，mi，Ti)，其中mi为当前卖出的彩票数量，Ti为timestamp。CC然后将Li=sign(，hi，ei，mi，Ti)发送给Alice，并将(，hi，ei，mi，Ti)在公告板上公布。

步骤6Alice在收到Li=sign(，hi，ei，mi，Ti)后，对照公告板上的信息，看是否一致，若不一致通过出示Li= sign(，hi，ei，mi，Ti)要求CC更正。

3.3 摇奖阶段

销售时间截止后，假设最后一共卖出M张票，那么对于每一张卖出的票都有对应的数对(,hi)其中i=1，2，…，M，然后CC按照如下步骤生成随机函数以及获奖数字。

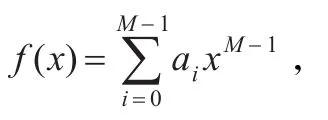
步骤2CC选取W=(a0，a1，…，at-1)作为中奖数字，即a0，a1，…，aM-1前t位（注：如果出现t＞M的情况，可将a0，a1，…，aM-1循环使用，即截取a0，a1，…，aM-1，a0，a1，…，aM-1，…的前t位）。

步骤3CC公布中奖数字。

3.4 领奖阶段

假设Alice赢得了彩票，按以下步骤兑奖：

步骤1Alice发送Li=sign(，hi，ei，mi，Ti)，di，ϕ(N)给CC。

步骤2CC在收到Alice发的信息后，做如下工作：

（1）对照Li=sign(，hi，ei，mi，Ti)是否与所公布的(，hi，ei，mi，Ti)一致；

（2）计算Wei看是否等于；

步骤3CC经过以上验证，若都成立，则确信Alice为中奖者。

步骤4CC公布Li，di，ϕ(N)，使所有人都可验证获奖者的真伪。

步骤5CC给Alice奖金。

4 本文方案分析

主要分析方案具有的安全性、公平性、可验证性，其他性质已经在Lee-Chang方案中得到了证明。

（1）安全性

定理1假设在实际购买者中没人中奖，而此时攻击者P试图伪造获奖彩票以获取奖金，这种攻击不可能成功。

证明首先因为整个过程都是公开的，所有卖出去的彩票(，hi，ei，mi，Ti)都在公告板上公布，每个人都可以验证是存在等于；并且在攻击者P公布自己中奖之后，所有人都可以验证P的(，hi)是否在多项式上，这样必然发现P是伪造者。

定理2假设攻击者P冒充获奖者Alice领取奖金，也必然失败。

证明因为获奖数字公布之后，获奖者需要发送（Li，di，φ(N)）给CC，而di是Alice的私钥，攻击者P无法获知。假设在Alice发送自己的信息给CC的过程中，信息被P截取，Alice最终仍然可以通过出示IDi以验证hi=Hash(IDi||Ai)，这样必然能发现P是冒充者。

（2）公平性

定理3在彩票销售结束前，任何人无法预测中奖数字。

证明中奖数字是由所有卖出的彩票对应的(，hi)来构造Zp上插值多项式得到的，该多项式由全部彩票数据决定，所有参与者具有同等的权值，中奖号码会根据购买者所选数字的改变而改变。

定理4卖票结束后，任何人不能修改所买彩票的数值。

证明首先，每个人买过彩票之后，其对应的数据被公布，整个过程是公开的，而且如果某人改变了自己的彩票值以试图获得奖金，那么其他人可以通过对照公告板上的值发现他的行为，而且在他修改过之后，其他参与者可以验证插值多项式f(x)是否通过，hi)，即f()=hi是否成立来判断彩票是否被修改。

（3）可验证性

定理5每个人可以验证随机函数是不是随机生成的，从而验证获奖数字生成的随机性。

证明买票者可以通过公告板上的信息独立计算f(x)，并独立验证f()=hi是否成立，不需要可信任第三方及其他人的协议，从而判断中奖数字是否公平公正。

定理6中奖者可以被公众验证其中奖事实。

证明假设Alice中奖，所有人可能通过检验是否成立。是Alice买票时在公告板上公布的信息；并且在CC公布过Alice的(Li，di，ϕ(N))后，其他人可以通过Alice的私钥di验证看是否等于W=(a0，a1，…，at-1)。

5 方案对比

通过Lee-Chang方案的漏洞分析和本文方案的安全性分析，可以知道本文新方案克服了Lee-Chang旧方案的不足：

（1）对于原方案的第一个漏洞，即种子w是由Countf模n得到的，导致中奖号码Ran(w)=CW={cw1,cw2,…,cwt}最多有n种可能性，当n较小时可以被穷举攻击。但是在本文方案中不存在这一问题，该方案中的随机函数由每位购买者共同生成，每一次的随机函数不一定相同，与每次所有购买者的彩票值有关，从而中奖号码不会受w范围和固定的随机函数Ran(*)的影响。

（2）本文方案克服了原方案的第二漏洞，任何人不能预测中奖号码，包括最后一个购买者也不能达到预测的目的。假设最后一名购买者E通过前面购买者的信息预测中奖号码，也必然失败。因为中奖号码是由所有彩票信息公共构造多项式后得到的，当E购买预测的号码后，计算出来的多项式也随之改变，从而中奖号码也和预测的不同。

6 总结

本文方案的最大特点就是整个过程是公开的，并且通过运用安全多方计算的思想，实现了相互验证，起到了相互监督的作用，以防止某方作弊。由于彩票活动涉及金额巨大，所以在公平公开的同时，其安全性至关重要。本文方案在支付购买彩票资金和奖金的发送方面没有进行阐述，今后有待于进一步完善。

[1]Chaum D.Untraceable electronic mail，return addresses and digital pseudonyms[J].Communications of the ACM，1981，24（2）：84-88.

[2]Cramer R，Franklin M，Schoenmakers B.Multi-authority secretballotelectionswithlinearwork[C]//Proceedingsofthe EUROCRYPT’96.Berlin：Springer-Verlag，1996，1070：72-83.

[3]Goldschlag D M，Stubblebine S G.Publicly variable lotteries：applicationsofdelayingfunctions[C]//Proceedingsofthe Financial Crypto 98，1998，1465：214-226.

[4]Lee J S，Chang C C.Design of electronic t-out-of-n lotteries on the Internet[J].Computer Standards and Interfaces，2009，31（2）：395-400.

[5]Gray D，Sheedy G.The security of Lee and Chang’s t-out-of-n lottery protocol[EB/OL].[2011-10-01].http：//www.computing.dcu. ie/wpapers/2009/0109.pdf.

[6]Du W，Atallah M J.Secure multi-party computation problems andtheirapplications：areviewandopenproblems[C]// Proceedings of the 2001 Workshop on New Security Paradigms，Cloudcroft，New Mexico，September 10-13，2001.

[7]Harn L，Lin C.Authenticated group key transfer protocol based on secret sharing[J].IEEE Transactions on Computers，2010，59（6）：842-846.

[8]Tzeng W G.A secure fault-tolerant conference-key agreement protocol[J].IEEE Transactions on Computers，2002，51（4）.

[9]Kim W H，Ryu E K，Im J Y，et al.New conference key agreementprotocolwithuseranonymity[J].ComputerStandards and Interfaces，2005，27（2）：185-190.

SUN Peiyong,LIU Yining,LI Yajun

School of Mathematics and Computing Science,Guilin University of Electronic Technology,Guilin,Guangxi 541004,China

In 2009,based on Chinese remainder theorem and blind signature,Lee and Chang proposed a electronic lottery protocol,but this protocol does not satisfy the requirement of fairness and verification.This paper proposes a electronic lottery protocol based on multi-party computation,and the winning numbers is generated by all the players.The improvement prevents dishonest participant from forging lottery ticket and makes the scheme public verification.

electronic lottery;multi-party computation;random function;public verification

2009年，Lee和Chang提出了基于中国剩余定理和盲签名的电子彩票方案，但其方案不满足公平性和公开可验证性。给出了一种基于安全多方计算的电子彩票协议，中奖号码由所有参与者共同产生，可防止合谋造假，并满足广泛的可验证性。

电子彩票；安全多方计算；随机函数；公开可验证性

A

TP309

10.3778/j.issn.1002-8331.1111-0023

SUN Peiyong,LIU Yining,LI Yajun.Public verifiable security electronic lottery protocol.Computer Engineering and Applications,2013,49（13）：68-70.

广西教育厅基金重点项目（No.201012MS081）；桂林电子科技大学科研基金（No.UF08014Y）。

孙培勇（1986—），男，硕士生，研究方向：信息安全；刘忆宁（1973—），男，博士，副教授，研究方向：应用密码学与信息安全；李亚军（1989—），女，硕士生。E-mail：ynliu@guet.edu.cn

2011-11-07

2012-01-02

1002-8331（2013）13-0068-03

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1723.096.html